《151道题带你快速梳理C++知识(3)--- 初阶函数递归专题》

🔥小龙报:个人主页
🎬作者简介:C++研发,嵌入式,机器人方向学习者

前言
本专栏聚焦算法题实战,系统讲解算法模块:以《c++编程》,《数据结构和算法》《基础算法》《算法实战》 等几个板块以题带点,讲解思路与代码实现,帮助大家快速提升代码能力
ps:本章节题目分两部分,比较基础笔者只附上代码供大家参考,其他的笔者会附上自己的思考和讲解,希望和大家一起努力见证自己的算法成长
序章
递归难理解抽象,很难想到递归的方式,这个不急,慢慢来
(1)目前阶段就是理解递归的执行流程,以及尝试简单的递归,能写出简单的递归代码就好。
(2)后续的数据结构还有算法课还会再继续深入的了解递归
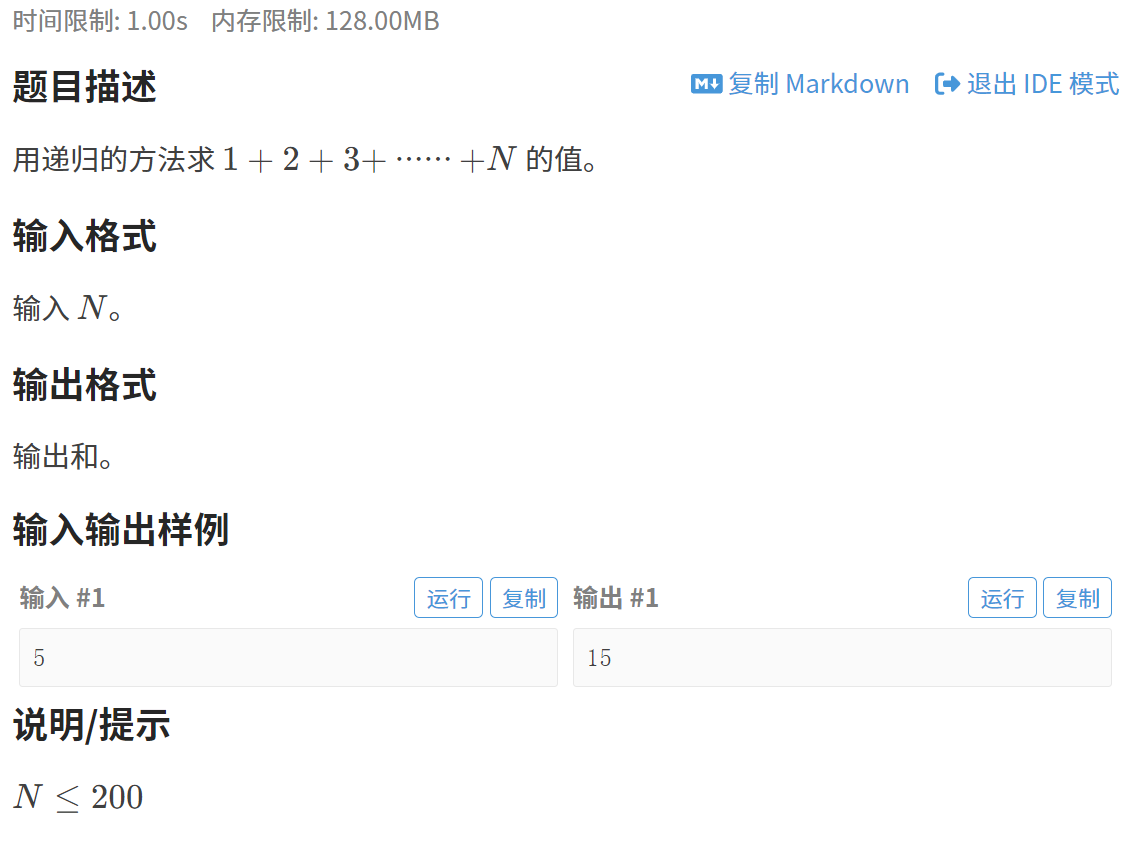
一、求 1+2+3+...+N 的值
1.1题目链接:求 1+2+3+...+N 的值
1.2题目解析
1.3代码:
c
#include <iostream>
using namespace std;
int sum(int n)
{
if(n == 1)
return 1;
return n + sum(n - 1);
}
int main()
{
int n;
cin >> n;
int ret = sum(n);
cout << ret << endl;
return 0;
}二、阿克曼(Ackermann)函数
2.1题目链接:阿克曼(Ackermann)函数
2.2题目解析

2.3代码:
c
#include <iostream>
using namespace std;
int A(int m,int n)
{
if(m == 0)
return n + 1;
else if(n == 0)
return A(m - 1,1);
else if(m > 0 && n > 0)
return A(m - 1,A(m,n - 1));
}
int main()
{
int m,n;
cin >> m >> n;
int ret = A(m,n);
cout << ret << endl;
return 0;
}三、digit函数
3.1题目链接:digit
3.2题目解析

分析:
如果n = 12345, k = 4, 要得到的是2
12345 的右起第4位 是2
1234 的右起第3位 是2
123 的右起第2位 是2
12 的右起第1位 是2
digit(n, k) --> digit(n / 10, k - 1)
截止条件,就是 k == 1的时候,结果就是n % 10
3.3代码:
c
#include <iostream>
using namespace std;
int digit(int n,int k)
{
if(k == 1)
return n % 10;
else
return digit(n / 10,k - 1);
}
int main()
{
int n,k;
cin >> n >> k;
int ret = digit(n,k);
cout << ret << endl;
return 0;
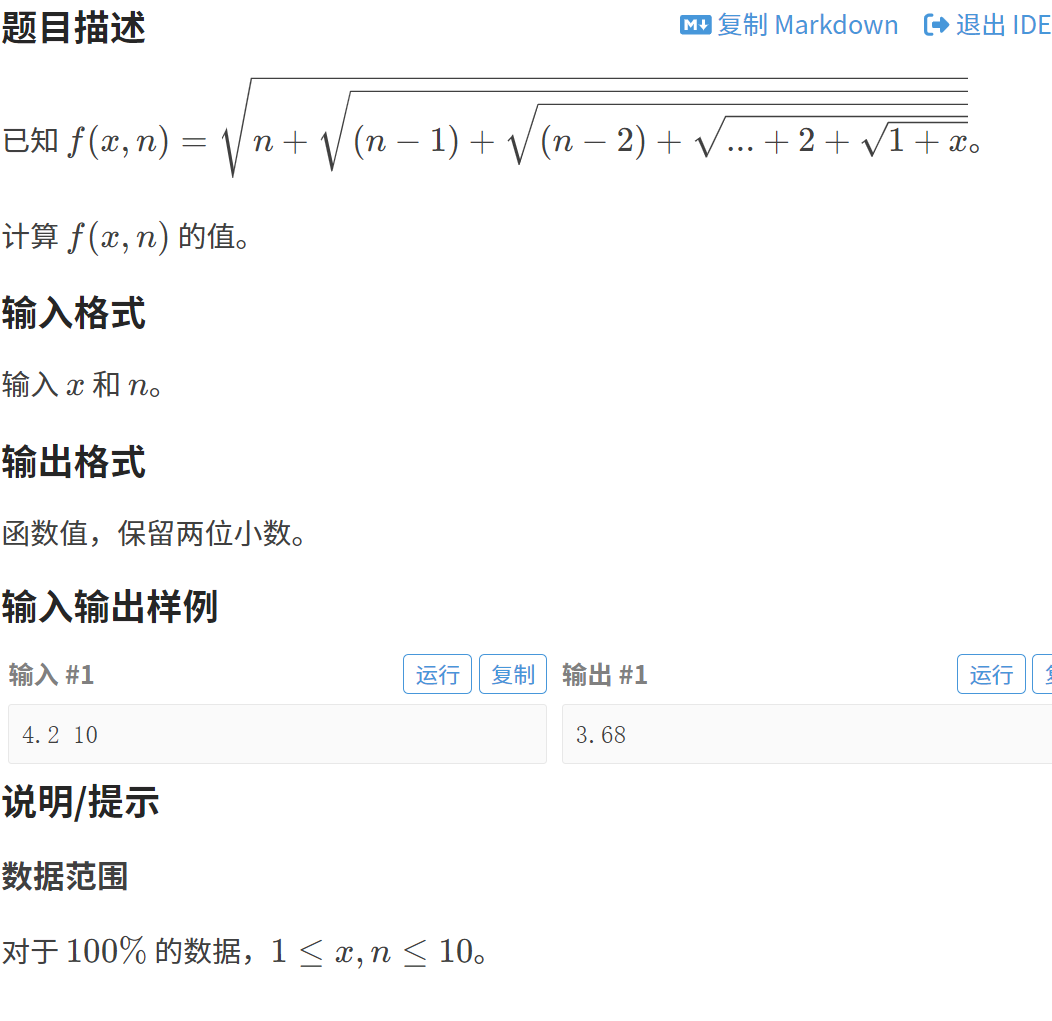
}四、求f(x,n)
4.1题目链接:求f(x,n)
4.2题目解析
4.3代码:
c
#include <cmath>
#include <iostream>
using namespace std;
double f(double x,int n)
{
if(n == 1)
return sqrt(1 + x);
else
return sqrt(n+f(x,n-1));
}
int main()
{
double x;
int n;
cin >> x >> n;
double op = f(x,n);
printf("%.2lf",op);
return 0;
}五、再求f(x,n)
5.1题目链接:再求f(x,n)
5.2题目解析

5.3代码:
c
#include <iostream>
using namespace std;
float f(float x, int n)
{
if (n == 1)
return x / (1 + x);
else
return x / (n + f(x, n - 1));
}
int main()
{
float x = 0;
int n = 0;
cin >> x >> n;
float ret = f(x, n);
printf("%.2f\n", ret);
return 0;
}六、进制转换
6.1题目链接:进制转换
6.2题目解析
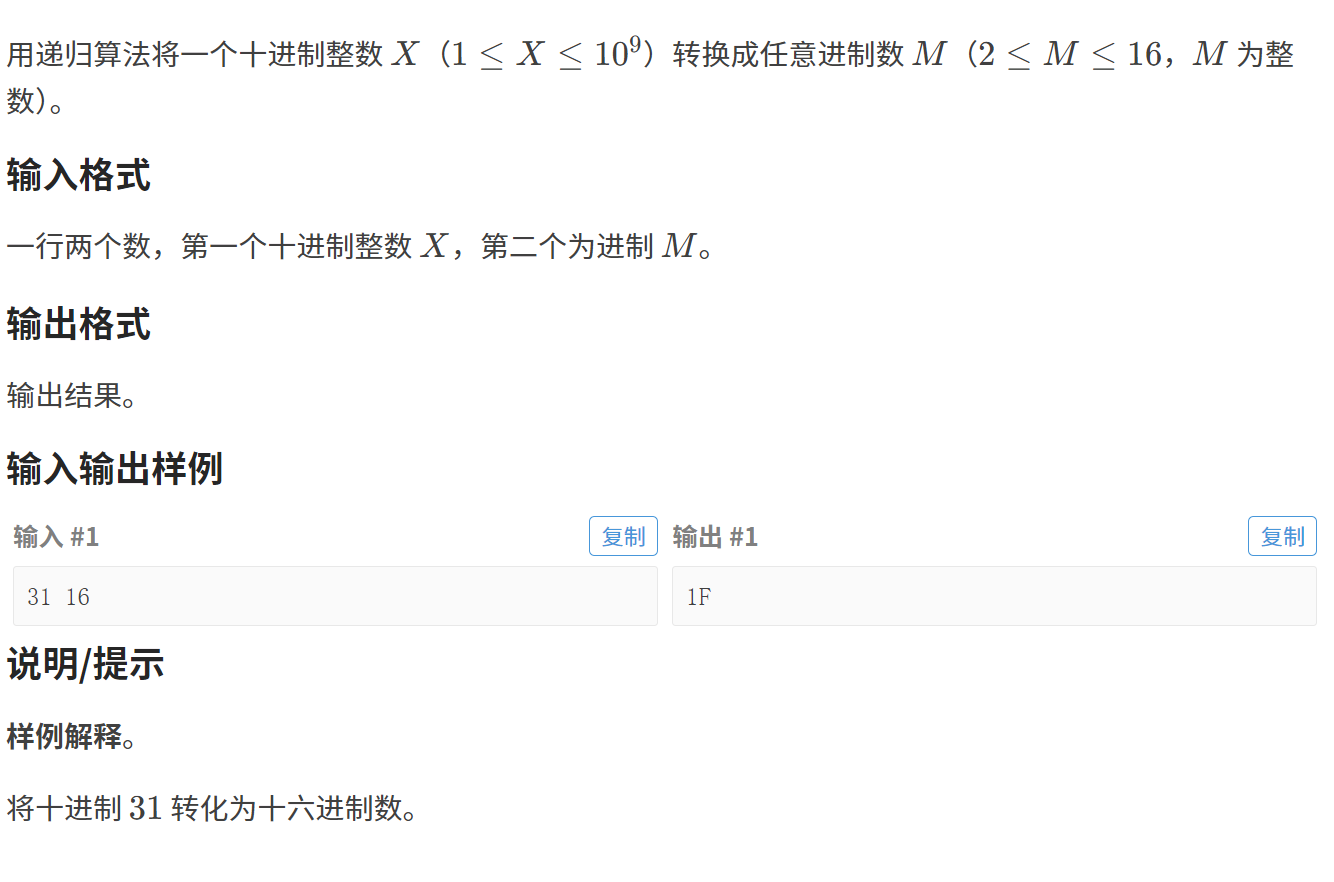
分析:
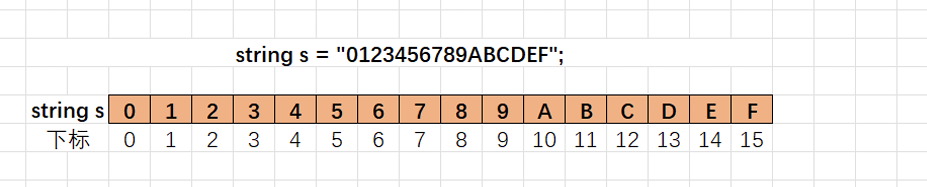

6.3代码:
c
#include <iostream>
using namespace std;
string s = "0123456789ABCDEF";
void to_x(int x,int m)
{
if(x >= m)
to_x(x / m,m);
cout << s[x % m];
}
int main()
{
int x,m;
cin >> x >> m;
to_x(x,m);
return 0;
}总结与每日励志
✨本文是C++函数递归专题的实战练习,通过6道经典题目帮助读者掌握递归思想。题目包括:1)计算1到N的和;2)实现阿克曼函数;3)提取数字特定位数;4)计算嵌套平方根函数;5)计算分数嵌套函数;6)实现进制转换。每道题都附有简洁的代码实现,特别适合初学者理解递归的基本思路和实现方法。文章强调递归需要循序渐进,建议先理解执行流程,再尝试简单递归代码。作者鼓励读者坚持练习,相信通过不断实践能够掌握递归这一重要编程思想
