【C++二叉搜索树】：从原理到实战的深度解析

月夜的风吹雨2025-11-20 11:25


🎬 博主名称 ：月夜的风吹雨
🔥 个人专栏 : 《C语言》《基础数据结构》《C++入门到进阶》

💬 前言

我们将手写完整实现，详解删除操作的四种情况，并对比key和key/value两种设计模式。当面试官问二叉搜索树，你将从容不迫，娓娓道来。

✨ 阅读后，你将掌握：

  • 二叉搜索树的精准定义与不变式
  • 插入、查找、删除的完整实现逻辑
  • 删除操作中替换法的深度剖析
  • key与key/value两种应用场景的本质区别
  • 二叉搜索树在STL中的演进路线

文章目录

  • 一、二叉搜索树⚖️
    • [1.1 什么是二叉搜索树？](#1.1 什么是二叉搜索树？)
    • [1.2 二叉搜索树 vs 二叉树 vs 堆](#1.2 二叉搜索树 vs 二叉树 vs 堆)
  • [二、性能分析：从最佳到最坏 ⚡](#二、性能分析：从最佳到最坏 ⚡)
    • [2.1 理想vs现实：树的形态决定性能](#2.1 理想vs现实：树的形态决定性能)
    • [2.2 二叉搜索树 vs 二分查找](#2.2 二叉搜索树 vs 二分查找)
  • 三、核心操作1：插入✍️
    • [3.1 插入算法](#3.1 插入算法)
    • [3.2 插入过程可视化](#3.2 插入过程可视化)
  • 四、核心操作2：查找🔍
    • [4.1 基本查找](#4.1 基本查找)
    • [4.2 查找中序第一个节点（处理重复值）](#4.2 查找中序第一个节点（处理重复值）)
  • [五、核心操作3：删除 🔥](#五、核心操作3：删除 🔥)
  • [六、完整实现：从节点到树 🌲](#六、完整实现：从节点到树 🌲)
    • [6.1 基础二叉搜索树实现](#6.1 基础二叉搜索树实现)
    • [6.2 复制构造与赋值运算符](#6.2 复制构造与赋值运算符)
  • [七、两种设计模式：key与key/value 🔄](#七、两种设计模式：key与key/value 🔄)
    • [7.1 key-only模式：搜索存在性](#7.1 key-only模式：搜索存在性)
    • [7.2 key/value模式：关联数据](#7.2 key/value模式：关联数据)
    • [7.3 key/value模式实现](#7.3 key/value模式实现)
  • [八、实战：单词频率统计器 📊](#八、实战：单词频率统计器 📊)
    • [8.1 问题描述](#8.1 问题描述)
    • [8.2 解决方案](#8.2 解决方案)
    • [8.3 性能分析](#8.3 性能分析)
  • [九、思考与总结 ✨](#九、思考与总结 ✨)
  • 十二、下篇预告

一、二叉搜索树⚖️

1.1 什么是二叉搜索树？

二叉搜索树(Binary Search Tree, BST)又称二叉排序树，它或者是空树，或者具有以下性质：

  1. 若左子树不为空，则左子树上所有节点的值都小于等于根节点的值
  2. 若右子树不为空，则右子树上所有节点的值都大于等于根节点的值
  3. 左右子树也分别为二叉搜索树
cpp 复制代码 
// 二叉搜索树节点定义
template<class K>
struct BSTNode {
    K _key;                  // 节点值
    BSTNode<K>* _left;       // 左孩子
    BSTNode<K>* _right;      // 右孩子
    
    BSTNode(const K& key)
        :_key(key), _left(nullptr), _right(nullptr) {}
};

💡 关键点：

  • 全局有序性：BST的有序性是递归定义的，不仅是直接子节点，而是整个子树
  • 可选择是否允许重复值：根据应用场景，可选择允许或禁止重复值
  • 非平衡特性：标准BST不保证平衡，这是与AVL树、红黑树的本质区别

1.2 二叉搜索树 vs 二叉树 vs 堆

特性 二叉树 二叉搜索树 堆
节点关系 无特定要求 左 ≤ 根 ≤ 右 父 ≤ 子（小堆）或 父 ≥ 子（大堆）
有序性 无序 全局有序 局部有序
查找效率 O(N) 平均 O(log N)，最坏 O(N) O(N)
应用场景 基础结构 快速查找 / 范围查询 优先级队列

二、性能分析：从最佳到最坏 ⚡

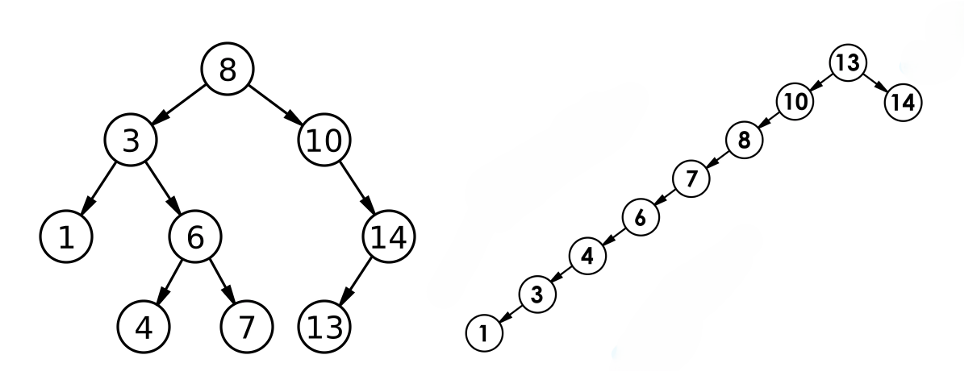
2.1 理想vs现实：树的形态决定性能

二叉搜索树 完全二叉树 退化成单支树

情况 树高 查找/插入/删除
理想情况：完全二叉树 O(log N) O(log N)
最坏情况：退化成链表 O(N) O(N)
平均情况：随机插入 O(log N) O(log N)

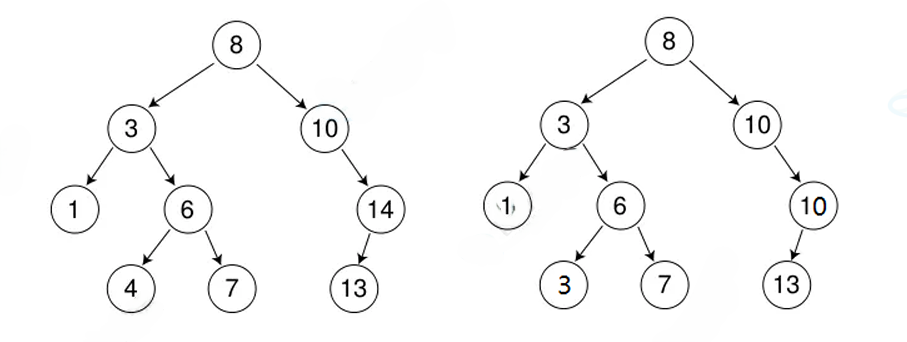
示例：

  • 插入序列：{8, 3, 1, 10, 6, 4, 7, 14, 13} → 生成平衡树
  • 插入序列：{1, 2, 3, 4, 5, 6, 7} → 退化成链表

2.2 二叉搜索树 vs 二分查找

二分查找也有O(logN)的时间复杂度，为何还需要二叉搜索树？

特性 二分查找 二叉搜索树
存储结构 顺序表(数组) 链式结构
插入效率 O(N) (需移动元素) O(log N) (仅修改指针)
删除效率 O(N) (需移动元素) O(log N) (仅修改指针)
空间要求 需要连续内存 无需连续内存
动态性 静态结构 动态结构

💡 核心价值：

二叉搜索树在保持 O ( l o g N ) O(logN) O(logN)查找效率的同时，提供了高效的动态插入和删除能力，完美平衡了静态结构与动态需求。

三、核心操作1：插入✍️

3.1 插入算法

插入操作相对简单，只需按照二叉搜索树的性质找到合适位置：

cpp 复制代码 
bool Insert(const K& key) {
    // 1. 空树，直接插入
    if(_root == nullptr) {
        _root = new Node(key);
        return true;
    }
    
    // 2. 非空树，寻找插入位置
    Node* parent = nullptr;
    Node* cur = _root;
    while(cur) {
        if(cur->_key < key) {
            parent = cur;
            cur = cur->_right;
        } else if(cur->_key > key) {
            parent = cur;
            cur = cur->_left;
        } else {
            // 3. 值已存在，插入失败
            return false;
        }
    }
    
    // 4. 创建新节点
    cur = new Node(key);
    if(parent->_key < key) {
        parent->_right = cur;
    } else {
        parent->_left = cur;
    }
    return true;
}

3.2 插入过程可视化

插入序列：{8, 3, 10, 1, 6, 14, 4, 7, 13}
1 3 4 6 7 8 10 13 14

💡 关键点：

  • 插入过程不修改已有节点
  • 不允许重复值时，找到相同值即返回失败
  • 允许重复值时，需要约定插入方向(通常插入右子树)

四、核心操作2：查找🔍

4.1 基本查找

cpp 复制代码 
bool Find(const K& key) {
    Node* cur = _root;
    while(cur) {
        if(cur->_key < key) {
            cur = cur->_right;
        } else if(cur->_key > key) {
            cur = cur->_left;
        } else {
            return true; // 找到
        }
    }
    return false; // 未找到
}

4.2 查找中序第一个节点（处理重复值）

当树中允许重复值时，通常需要查找中序遍历中的第一个匹配节点：

cpp 复制代码 
Node* FindFirst(const K& key) {
    Node* cur = _root;
    Node* result = nullptr;
    
    while(cur) {
        if(cur->_key < key) {
            cur = cur->_right;
        } else if(cur->_key > key) {
            cur = cur->_left;
        } else {
            // 找到匹配，继续搜索更左的节点
            result = cur;
            cur = cur->_left;
        }
    }
    return result;
}

💡 思考：

为什么查找比插入简单？

查找不修改树结构，只需按值遍历路径。这也是为什么大多数操作都从查找开始------它是其他操作的基础。

五、核心操作3：删除 🔥

5.1 删除操作的四种情况

删除是二叉搜索树中最复杂的操作，需要处理四种情况：

情况1&2&3：0-1个子节点

  1. 叶子节点：直接删除
  2. 只有左子树：父节点指向左子树
  3. 只有右子树：父节点指向右子树
cpp 复制代码 
// 0-1个孩子的情况
if(cur->_left == nullptr) {
    // 只有右子树或无子树
    if(parent == nullptr) {
        _root = cur->_right;
    } else {
        if(parent->_left == cur) {
            parent->_left = cur->_right;
        } else {
            parent->_right = cur->_right;
        }
    }
    delete cur;
    return true;
} else if(cur->_right == nullptr) {
    // 只有左子树
    if(parent == nullptr) {
        _root = cur->_left;
    } else {
        if(parent->_left == cur) {
            parent->_left = cur->_left;
        } else {
            parent->_right = cur->_left;
        }
    }
    delete cur;
    return true;
}

情况4：2个子节点（替换法删除）

当节点有两个子节点时，无法直接删除，需用替换法：

  1. 找到右子树的最小节点(最左节点)或左子树的最大节点(最右节点)
  2. 交换值，将问题转化为删除只有一个子节点的节点
cpp 复制代码 
// 2个孩子的情况 - 替换法删除
Node* rightMinP = cur;
Node* rightMin = cur->_right;
while(rightMin->_left) {
    rightMinP = rightMin;
    rightMin = rightMin->_left;
}
// 交换值
cur->_key = rightMin->_key;

// 删除rightMin节点
if(rightMinP->_left == rightMin) {
    rightMinP->_left = rightMin->_right;
} else {
    rightMinP->_right = rightMin->_right;
}
delete rightMin;
return true;

5.2 替换法删除的深入解析

替换法是二叉搜索树删除操作的核心难点，让我们深入分析：
1 3 4 6 7 8 10 13 14

删除8的步骤：

  • 找到右子树(10)的最小节点13
  • 交换8和13的值
  • 删除原13的位置（此时13是叶子节点，直接删除）

1 3 4 6 7 10 13 14

💡 为什么选择右子树最小节点 或左子树最大节点？

  • 保证替换后的值仍然大于左子树所有节点
  • 保证替换后的值仍然小于右子树除替换节点外的所有节点
  • 右子树最小节点一定没有左子节点（是叶子或只有右子节点）

⚠️ 常见错误：
rightMinP = cur; 这行代码至关重要！当右子树根节点就是最小节点时（没有左孩子），rightMinP 需指向 cur 而非 cur->_right ，否则无法正确处理替换后指针连接。

六、完整实现：从节点到树 🌲

6.1 基础二叉搜索树实现

cpp 复制代码 
template<class K>
class BSTree {
    typedef BSTNode<K> Node;
public:
    BSTree() : _root(nullptr) {}
    
    // 插入
    bool Insert(const K& key);
    
    // 查找
    bool Find(const K& key);
    
    // 删除
    bool Erase(const K& key);
    
    // 中序遍历
    void InOrder() { _InOrder(_root); cout << endl; }
    
    ~BSTree() {
        _Destroy(_root);
        _root = nullptr;
    }
private:
    void _InOrder(Node* root) {
        if(root == nullptr) return;
        _InOrder(root->_left);
        cout << root->_key << " ";
        _InOrder(root->_right);
    }
    
    void _Destroy(Node* root) {
        if(root == nullptr) return;
        _Destroy(root->_left);
        _Destroy(root->_right);
        delete root;
    }
    
    Node* _root;
};

6.2 复制构造与赋值运算符

为遵循C++的"三大法则"，需要实现拷贝构造和赋值运算符：

cpp 复制代码 
BSTree(const BSTree<K>& t) {
    _root = _Copy(t._root);
}

BSTree<K>& operator=(BSTree<K> t) {
    swap(_root, t._root);
    return *this;
}

Node* _Copy(Node* root) {
    if(root == nullptr) return nullptr;
    Node* newRoot = new Node(root->_key);
    newRoot->_left = _Copy(root->_left);
    newRoot->_right = _Copy(root->_right);
    return newRoot;
}

💡 现代C++技巧：

赋值运算符使用拷贝-交换技巧实现强异常安全，接收参数时使用值传递，充分利用移动语义。

七、两种设计模式：key与key/value 🔄

7.1 key-only模式：搜索存在性

特点：

  • 仅存储键值
  • 适用于判断元素是否存在
  • 不允许修改键值（会破坏BST性质）
cpp 复制代码 
// 小区无人值守车库
class ParkingSystem {
private:
    BSTree<string> _licensePlates; // 存储已授权车牌
public:
    bool CanEnter(const string& licensePlate) {
        return _licensePlates.Find(licensePlate);
    }
    
    void AddAuthorizedPlate(const string& licensePlate) {
        _licensePlates.Insert(licensePlate);
    }
};

7.2 key/value模式：关联数据

特点：

  • 存储键值对
  • 可修改value值，但不能修改key
  • 适合需要关联数据的场景
cpp 复制代码 
// 商场无人值守车库
class MallParking {
private:
    struct EntryRecord {
        string licensePlate;
        time_t entryTime;
    };
    BSTree<string, time_t> _records; // 车牌 -> 入场时间
    
public:
    void RecordEntry(const string& licensePlate) {
        _records.Insert(licensePlate, time(nullptr));
    }
    
    double CalculateFee(const string& licensePlate) {
        auto record = _records.Find(licensePlate);
        if(!record) return 0.0;
        
        time_t now = time(nullptr);
        double hours = difftime(now, record->_value) / 3600.0;
        return min(hours, 24.0) * 5.0; // 每小时5元，每天封顶
    }
};

7.3 key/value模式实现

cpp 复制代码 
template<class K, class V>
struct BSTNode {
    K _key;
    V _value;
    BSTNode<K, V>* _left;
    BSTNode<K, V>* _right;
    
    BSTNode(const K& key, const V& value)
        : _key(key), _value(value), _left(nullptr), _right(nullptr) {}
};

template<class K, class V>
class BSTree {
    typedef BSTNode<K, V> Node;
public:
    bool Insert(const K& key, const V& value);
    Node* Find(const K& key); // 返回节点指针，可修改value
    bool Erase(const K& key);
    
    // 修改value
    bool Update(const K& key, const V& newValue) {
        Node* node = Find(key);
        if(node) {
            node->_value = newValue;
            return true;
        }
        return false;
    }
};

💡 关键设计：

  • Find 返回节点指针而非bool，允许直接修改value
  • 不能提供修改key的接口，会破坏BST性质
  • 更新操作应通过先查找再修改实现，避免重复代码

八、实战：单词频率统计器 📊

8.1 问题描述

统计一篇文章中每个单词出现的频率，并按单词字母顺序输出。

8.2 解决方案

cpp 复制代码 
int main() {
    string arr[] = {"苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", 
                   "西瓜", "苹果", "香蕉", "苹果", "香蕉"};
    BSTree<string, int> countTree;
    
    for(const auto& str : arr) {
        auto ret = countTree.Find(str);
        if(ret == nullptr) {
            // 第一次出现
            countTree.Insert(str, 1);
        } else {
            // 已存在，计数+1
            ret->_value++;
        }
    }
    
    countTree.InOrder(); // 中序遍历自动按字母顺序输出
    return 0;
}

输出：

text 复制代码 
苹果:6
西瓜:3
香蕉:2

8.3 性能分析

  • 时间复杂度： O ( N l o g M ) O(N log M) O(NlogM)，N是总单词数，M是不同单词数
  • 空间复杂度： O ( M ) O(M) O(M)，M是不同单词数
  • 优势：中序遍历自动按字母顺序输出，无需额外排序

💡 为什么用BST而非哈希表？

虽然哈希表平均 O ( 1 ) O(1) O(1)的插入和查找效率更高，但BST在以下场景更优：

  • 需要按顺序输出结果
  • 内存受限且节点较小
  • 需要范围查询（如查找所有以"ap"开头的单词）

九、思考与总结 ✨

核心概念 关键理解
BST不变式 左≤根≤右的全局性质是BST所有操作的基础
删除操作 替换法是删除有两个子节点的核心技巧
平衡性 普通BST不保证平衡，可能导致性能退化
key模式 仅检查存在性，不允许修改key
key/value模式 存储关联数据，允许修改value但不能修改key
应用价值 BST是红黑树、AVL树等平衡树的基础

💡 一句话总结：

"二叉搜索树不仅是数据结构，更是一种思维方式------通过分而治之，将无序化为有序，将复杂问题分解为可管理的小问题。"

十二、下篇预告

下一篇《C++ map与set：关联式容器的深度探索》中，我们将：

  • 揭秘STL中map和set的底层实现
  • 深入理解红黑树如何解决BST的平衡问题
  • 掌握map的operator[]多用途接口设计哲学
  • 对比map/set与unordered_map/unordered_set的适用场景
  • 用关联容器解决力扣高频难题
相关推荐
xlq223224 小时前
15.list（上）
数据结构·c++·list
云帆小二4 小时前
从开发语言出发如何选择学习考试系统
开发语言·学习
光泽雨5 小时前
python学习基础
开发语言·数据库·python
Elias不吃糖5 小时前
总结我的小项目里现在用到的Redis
c++·redis·学习
AA陈超6 小时前
使用UnrealEngine引擎，实现鼠标点击移动
c++·笔记·学习·ue5·虚幻引擎
百***06016 小时前
python爬虫——爬取全年天气数据并做可视化分析
开发语言·爬虫·python
jghhh016 小时前
基于幅度的和差测角程序
开发语言·matlab
fruge6 小时前
自制浏览器插件：实现网页内容高亮、自动整理收藏夹功能
开发语言·前端·javascript
No0d1es6 小时前
电子学会青少年软件编程（C/C++）六级等级考试真题试卷（2025年9月）
c语言·c++·算法·青少年编程·图形化编程·六级
曹牧6 小时前
Java中处理URL转义并下载PDF文件
java·开发语言·pdf
热门推荐
01GitHub 镜像站点02今天 Cloudflare 全球事故，连 GPT 和你的网站都一起“掉线”了03UV安装并设置国内源04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05BongoCat - 跨平台键盘猫动画工具06Linux下V2Ray安装配置指南07全球最强模型Grok4，国内已可免费使用！（附教程）08Valdi：Snapchat 开源的新一代跨平台 UI 框架09Labelme从安装到标注：零基础完整指南10swagger xss漏洞复现