目录
- 前言
- 一、删除有序数组中的重复项
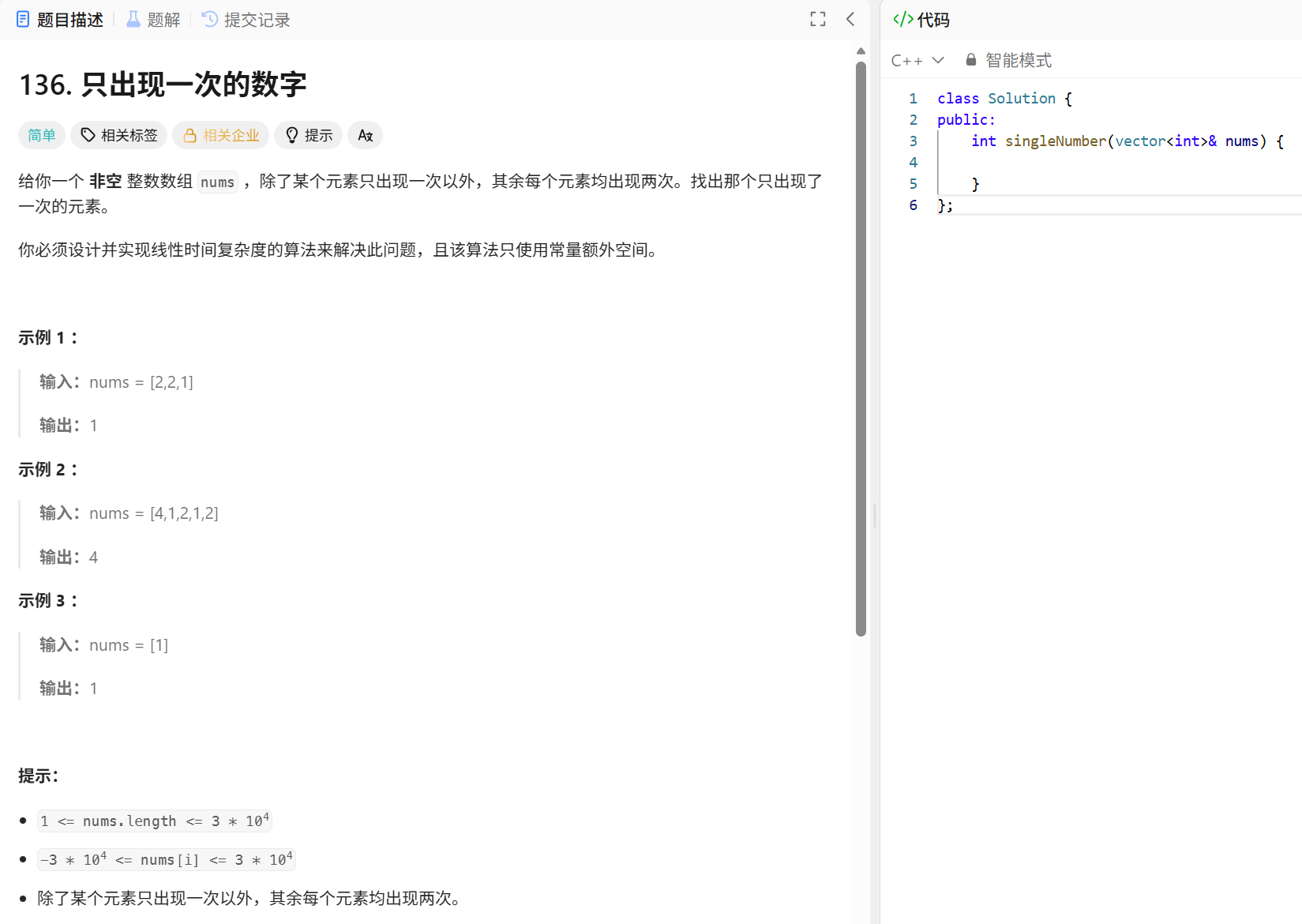
- 二、只出现一次的数字
- [三、只出现一次的数组 ||](#三、只出现一次的数组 ||)
- [四、只出现一次的数字 |||](#四、只出现一次的数字 |||)
- 五、数组中出现次数超过一半的数字
- 六、电话号码的字母组合
- 结语


🎬 云泽Q :个人主页
🔥 专栏传送入口 : 《C语言》《数据结构》《C++》《Linux》
⛺️遇见安然遇见你,不负代码不负卿~
前言
大家好啊,我是云泽Q,欢迎阅读我的文章,一名热爱计算机技术的在校大学生,喜欢在课余时间做一些计算机技术的总结性文章,希望我的文章能为你解答困惑~
一、删除有序数组中的重复项
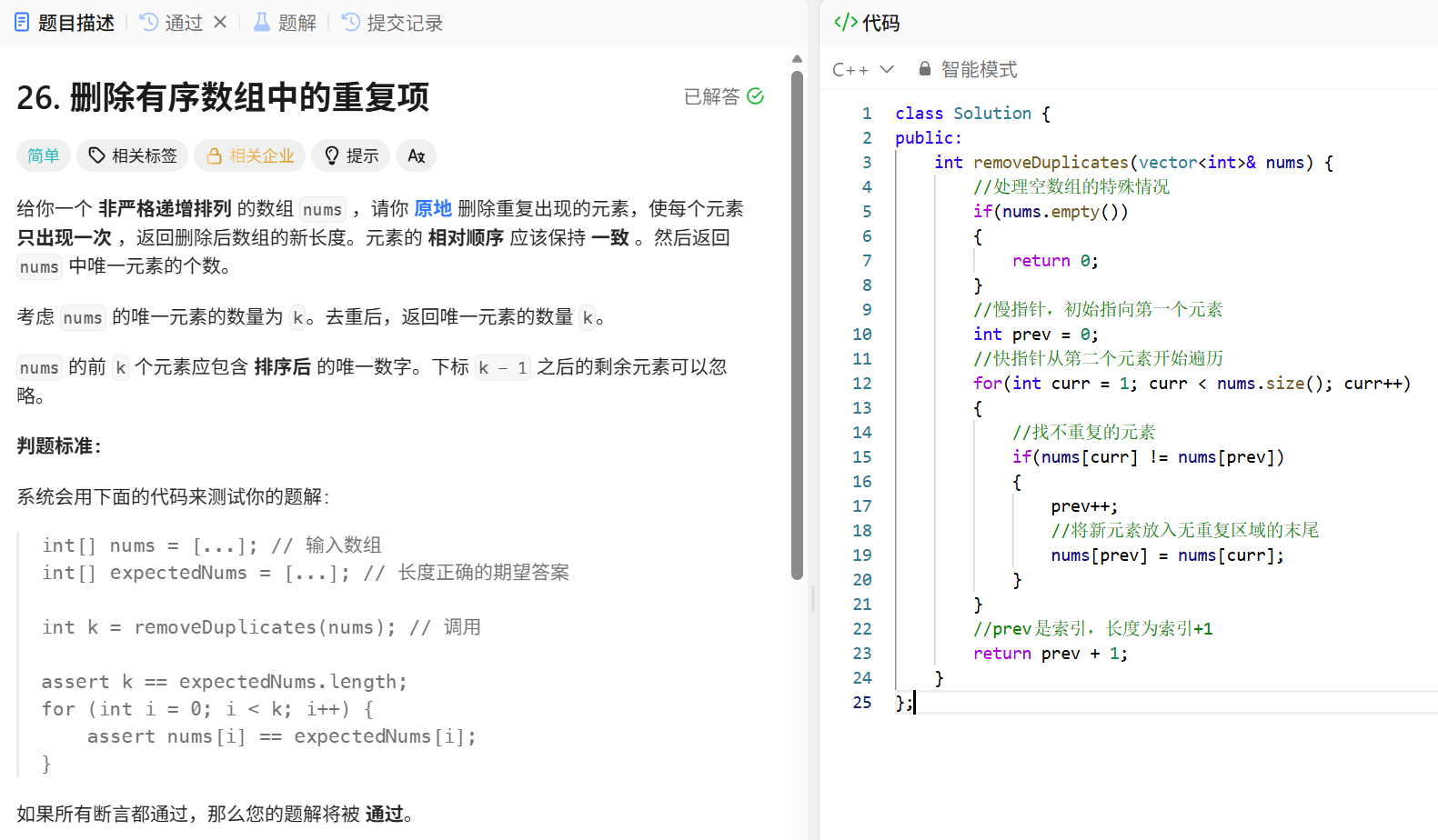
解题思路
由于数组是非严格递增的,重复的元素必然是相邻的。我们可以用两个指针:
- 慢指针 prev:标记 "已处理的无重复元素" 的最后一个位置。
- 快指针 curr:遍历数组,寻找新的、未出现过的元素。
结合 示例 1(输入nums = [1,1,2]) 拆解解题过程:
步骤 1:初始化指针
- 慢指针 prev 初始化为 0(指向数组第一个元素 1)。
- 快指针 curr 初始化为 1(从第二个元素开始遍历)。
步骤 2:第一次循环(curr = 1)
此时 nums[curr] = 1,nums[prev] = 1,两者相等。
- 因为元素重复,不需要更新nums,仅将 curr 后移(curr = 2)。
- 数组状态仍为 [1, 1, 2]。
步骤 3:第二次循环(curr = 2)
此时 nums[curr] = 2,nums[prev] = 1,两者不相等。
- 先将 prev 后移(prev = 1)。
- 把 nums[curr] 的值(2)赋给 nums[prev],此时数组变为 [1, 2, 2]。
- 再将 curr 后移(curr = 3),此时 curr 超出数组长度,循环结束。
步骤 4:返回结果最终 prev = 1,无重复元素的数量为 prev + 1 = 2,与示例输出一致。数组的前 2 个元素为 [1, 2],满足题目要求。
尤其注意:慢指针 prev 最终指向的是 "无重复元素区域" 的最后一个元素的索引,需要返回的是无重复元素的数量
通过这样的步骤,双指针法在原地完成了重复元素的删除,同时保证了时间复杂度为O(n)、空间复杂度为 O(1),是该问题的最优解法。
二、只出现一次的数字
写这道题要清楚异或运算的特性:
异或运算(^)是基于二进制位的操作,规则是:对应二进制位相同则为 0,不同则为 1
c
3 的二进制:011(8 位表示为 00000011)
5 的二进制:101(8 位表示为 00000101)
合并结果为 00000110,即十进制的 6。所以 3 ^ 5 = 6性质 1:相同的数异或,结果为 0。例如 2 ^ 2 = 0,5 ^ 5 = 0。
性质 2:0 和任意数异或,结果为这个数本身。例如 0 ^ 3 = 3,0 ^ 99 = 99
异或元素还满足:交换律:a ^ b = b ^ a(异或的顺序不影响结果)。
结合律:(a ^ b) ^ c = a ^ (b ^ c)(可以任意调整异或的组合顺序)
c
4 ^ 1 ^ 2 ^ 1 ^ 2 = (1 ^ 1) ^ (2 ^ 2) ^ 4 = 0 ^ 0 ^ 4 = 4基于以上特性得出结论:只要元素是 "成对出现" 的,无论其数值是多少,异或后都会相互抵消(结果为 0);而唯一不成对的元素,会在最终异或中被保留下来
三、只出现一次的数组 ||
只出现一次的数组 ||
思路分析
数组中除一个元素外,其余元素都恰好出现三次。对于二进制的每一位来说,出现三次的元素在该位上的 1 的个数是 3 的倍数,而只出现一次的元素在该位上的 1 会 "打破" 这个倍数关系。因此,我们可以:
- 统计每一位二进制位上 1 出现的总次数。
- 对每个位的次数 对 3 取余,余数即为只出现一次的元素在该位上的取值(0 或 1)。
- 将所有位的结果组合,得到最终答案。
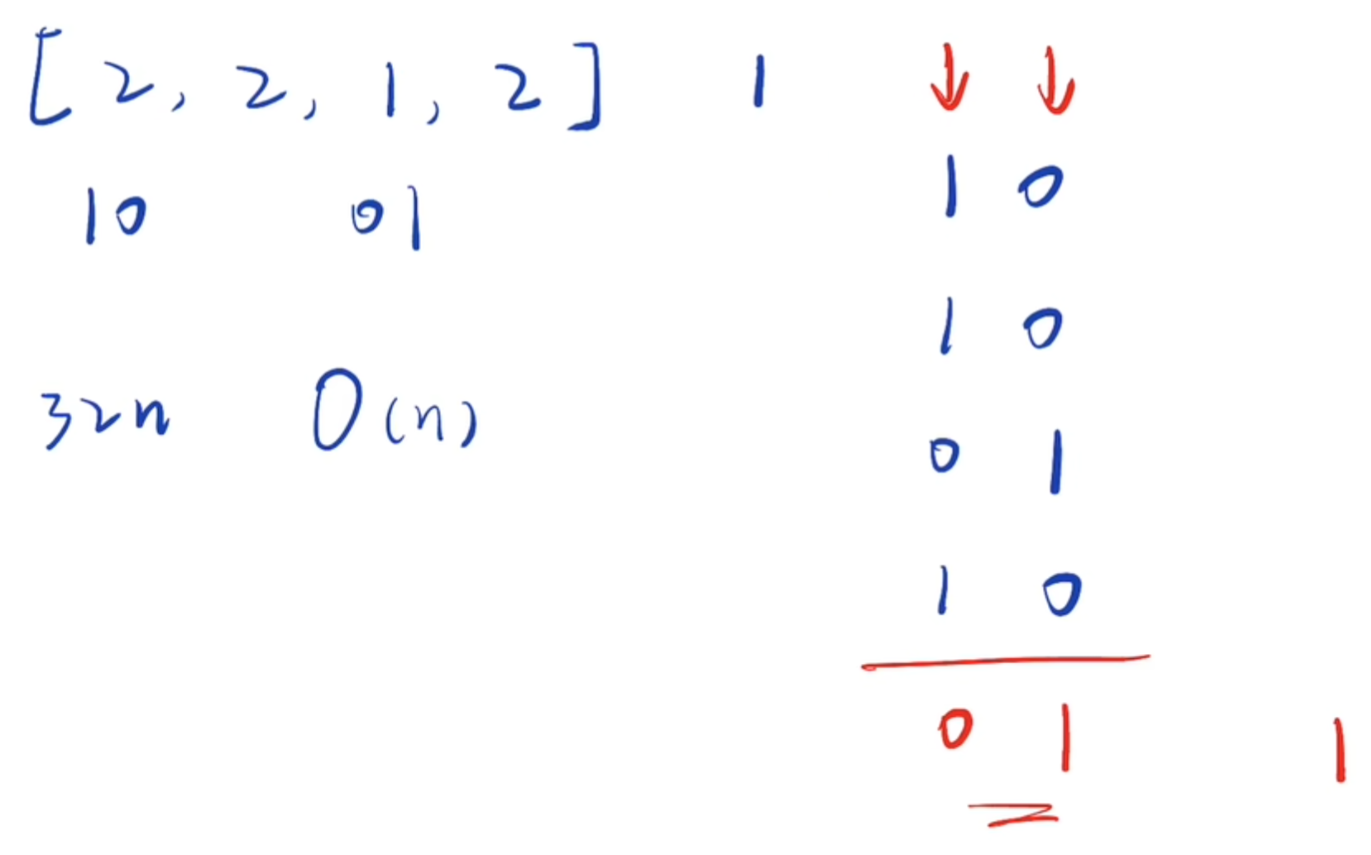
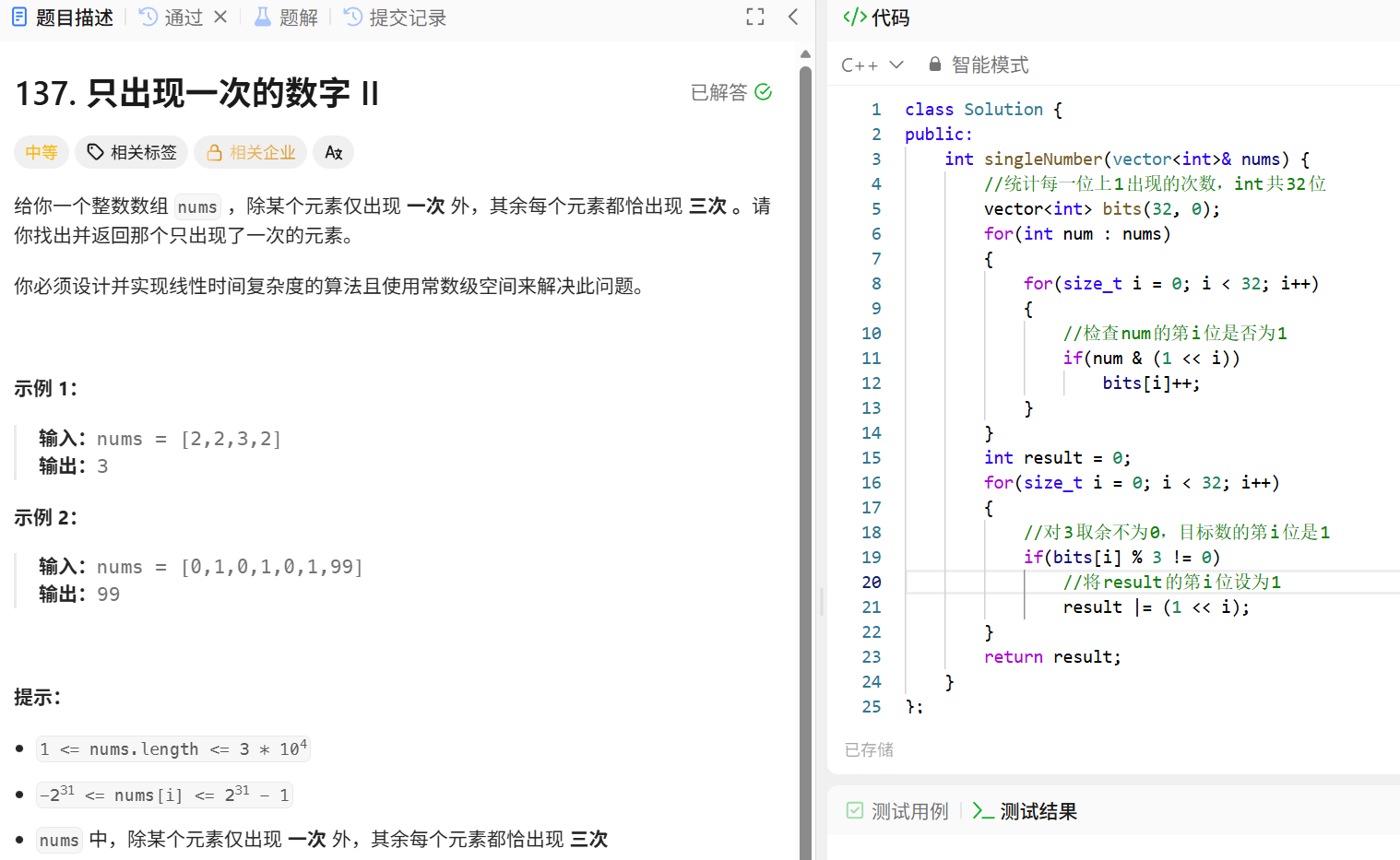
代码解释
- 统计每一位的 1 的次数:
-
- 初始化长度为 32 的数组 bits,用于记录每一位二进制位上 1 出现的次数。
-
- 遍历数组 nums 中的每个数 num,对每个数的每一位(0 到 31 位)进行检查,若该位为 1,则对应 bits 数组的计数加 1。
- 构建结果:
-
- 遍历 bits 数组,对每一位的计数 对 3 取余。若余数不为 0,说明只出现一次的元素在该位上为 1,通过 result |= (1 << i) 将该位设为 1。
-
- 最终 result 即为只出现一次的元素。
详细处理:



补充:符号位的作用是区分存储数据的正负
如果忽略符号位,只统计低 31 位,当目标元素是负数时,就会丢失符号位的信息,导致结果错误。
举个例子:假设目标元素是 -1,它的 32 位补码是 11111111 11111111 11111111 11111111(32 个1)。如果不统计符号位(第 31 位),统计结果会忽略最高位的1,最终得到的结果就会是一个正数(而非-1),显然错误。
因此,为了正确处理所有可能的整数(包括负数),必须统计全部 32 位(包含符号位),这样才能通过每一位的 "次数对 3 取余" 逻辑,准确还原出目标元素的二进制表示(包括符号位)。
四、只出现一次的数字 |||
只出现一次的数字 |||
思路分析
- 异或的核心特性 :两个相同的数异或结果为 0,一个数与 0 异或结果为其本身。因此,将数组中所有数异或后,结果是两个只出现一次的数的异或值(记为 xorSum)------ 因为其余出现两次的数会相互抵消。
- 分组的关键 :xorSum 中至少有一位是 1(因为两个目标数不同)。我们找到 xorSum 中最右边的 1 所在的位置 mask,并根据这个 mask 将数组分成两组:
-
- 组 1:该位为 1 的数;
-
- 组 2:该位为 0 的数。
这样,两个目标数会被分到不同组中,且每组内其余数都是成对出现的。
- 组 2:该位为 0 的数。
- 分别异或得结果:对两组数分别进行异或操作,最终得到的两个结果就是那两个只出现一次的数。
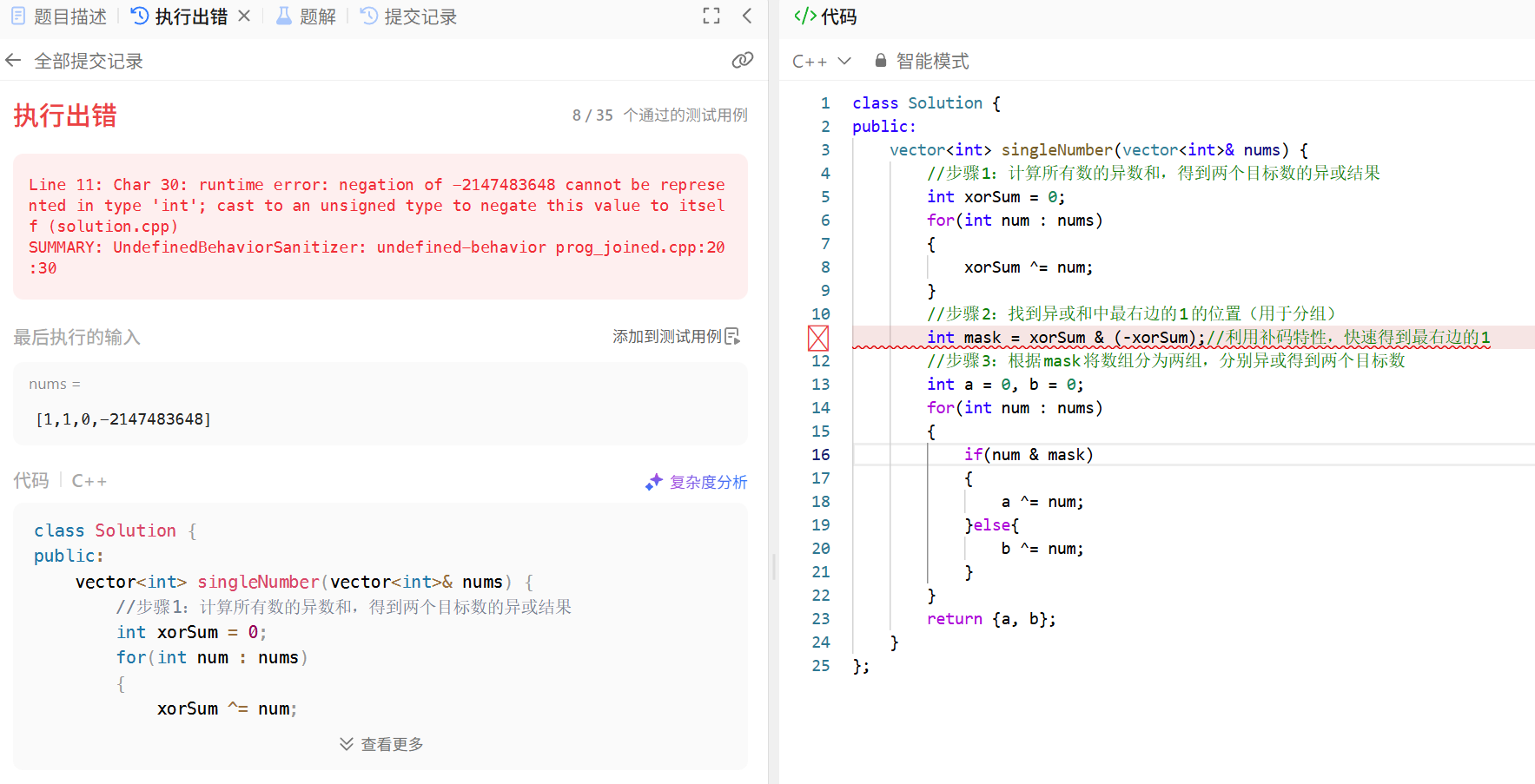
代码解释
- 步骤 1:计算异或和 xorSum
遍历数组,将所有数异或。由于出现两次的数会相互抵消(a ^ a = 0),最终 xorSum 是两个目标数的异或结果(x ^ y,其中 x 和 y 是要找的两个数)。 - 步骤 2:确定分组掩码 mask
xorSum & (-xorSum) 是一个常用技巧:利用补码的特性,得到 xorSum 中最右边的 1 所在的位。例如,若 xorSum = 6(二进制 110),则 -6 的二进制是 ...11111010(补码),6 & (-6) = 10(二进制 2),即最右边的 1 在第 1 位(从 0 开始计数)。 - 步骤 3:分组异或
遍历数组时,用 num & mask 判断数的第 mask 位是否为 1,将数分为两组。每组内的数异或后,出现两次的数会抵消,最终得到两个目标数 a 和 b。
下面是结合样例的详细分析:

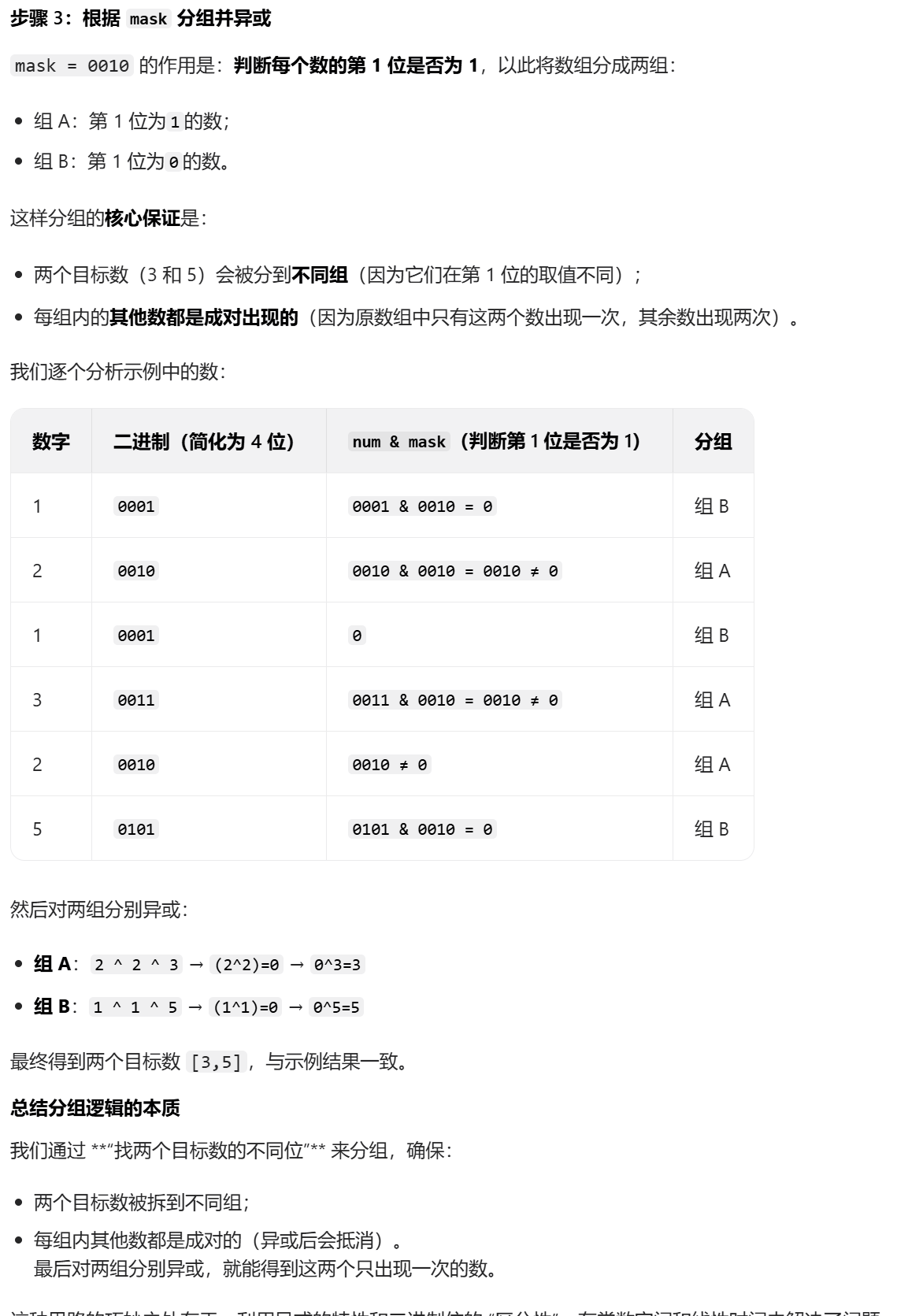
再说一下最后为什么可以直接返回{3, 4};
在 C++ 中,return {a, b} 会返回一个 vector< int > 类型的对象(可以理解为动态数组),其内部包含两个元素 a 和 b。
具体原因 :
函数的返回类型是 vector(题目要求返回 "两个只出现一次的数字组成的数组"),而 C++ 支持用初始化列表(即 {} 包裹的元素)来构造 vector 对象。
当执行 return {a, b} 时,编译器会自动将初始化列表 {a, b} 转换为一个 vector< int > 实例,其中第一个元素是 a,第二个元素是 b,符合函数的返回类型要求。
结合样例 :
在示例 nums = [1,2,1,3,2,5] 中,最终 a=3、b=5,return {a, b} 会返回一个 vector< int >,内容为 [3, 5],这正是题目所需的结果。
但是也可以看到上面的代码只通过了8个测试用例:
要解决这个运行时错误,我们需要处理int 类型最小值的取反溢出问题。以下是原因分析和修正方案:
错误原因
-2147483648 是 32 位有符号 int 的最小值(即 -231)。当对它取反时,-(-2147483648) = 2147483648,但 32 位有符号 int 的最大值是 2147483647(即 231-1),因此这个值无法用有符号 int 表示 ,导致溢出和未定义行为。
解决方案
将 xorSum 转换为无符号整数(unsigned int/size_t)后再计算 mask,因为无符号整数的范围更大(0 ~ 232-1),可以避免溢出。
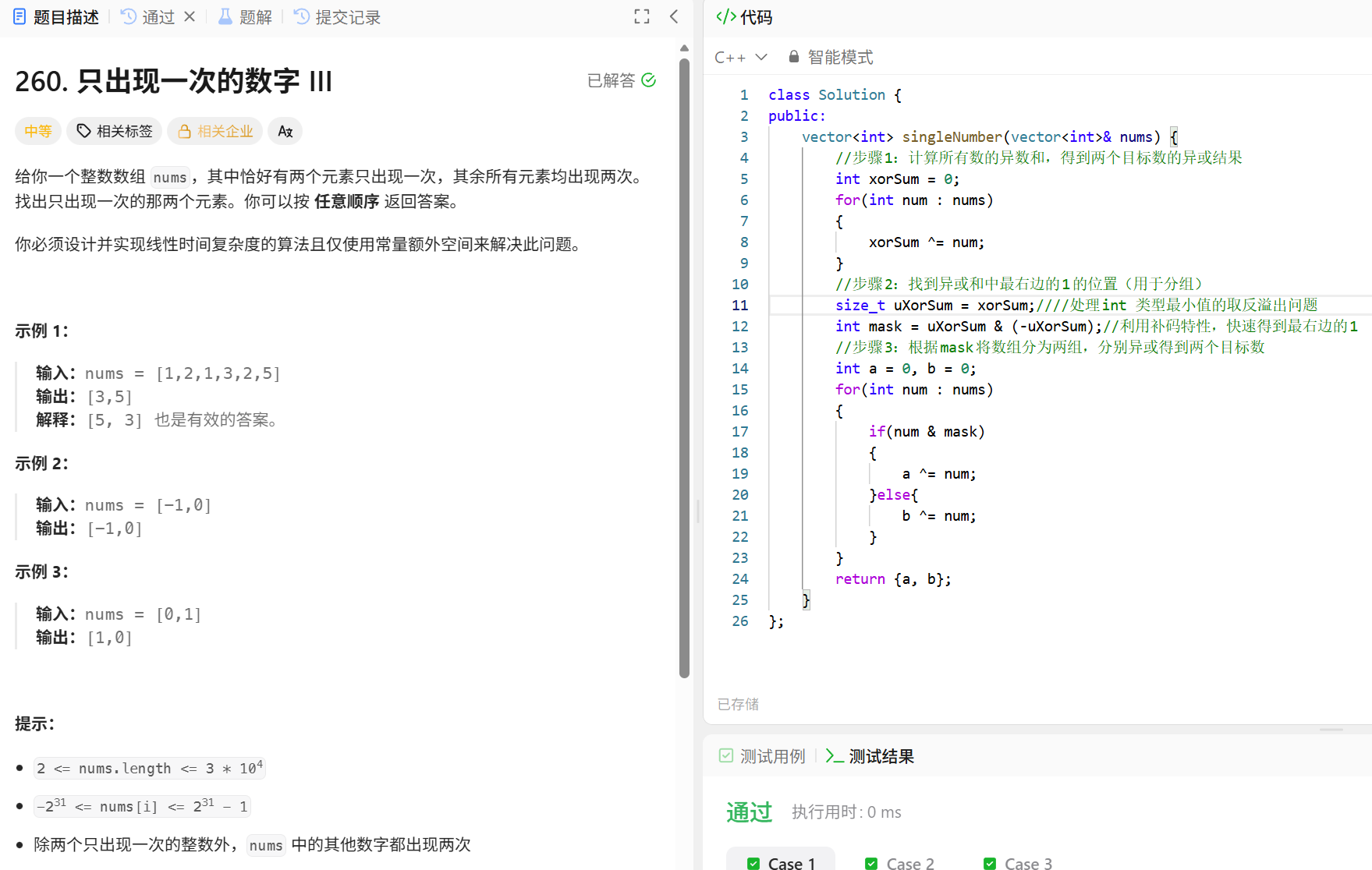
五、数组中出现次数超过一半的数字
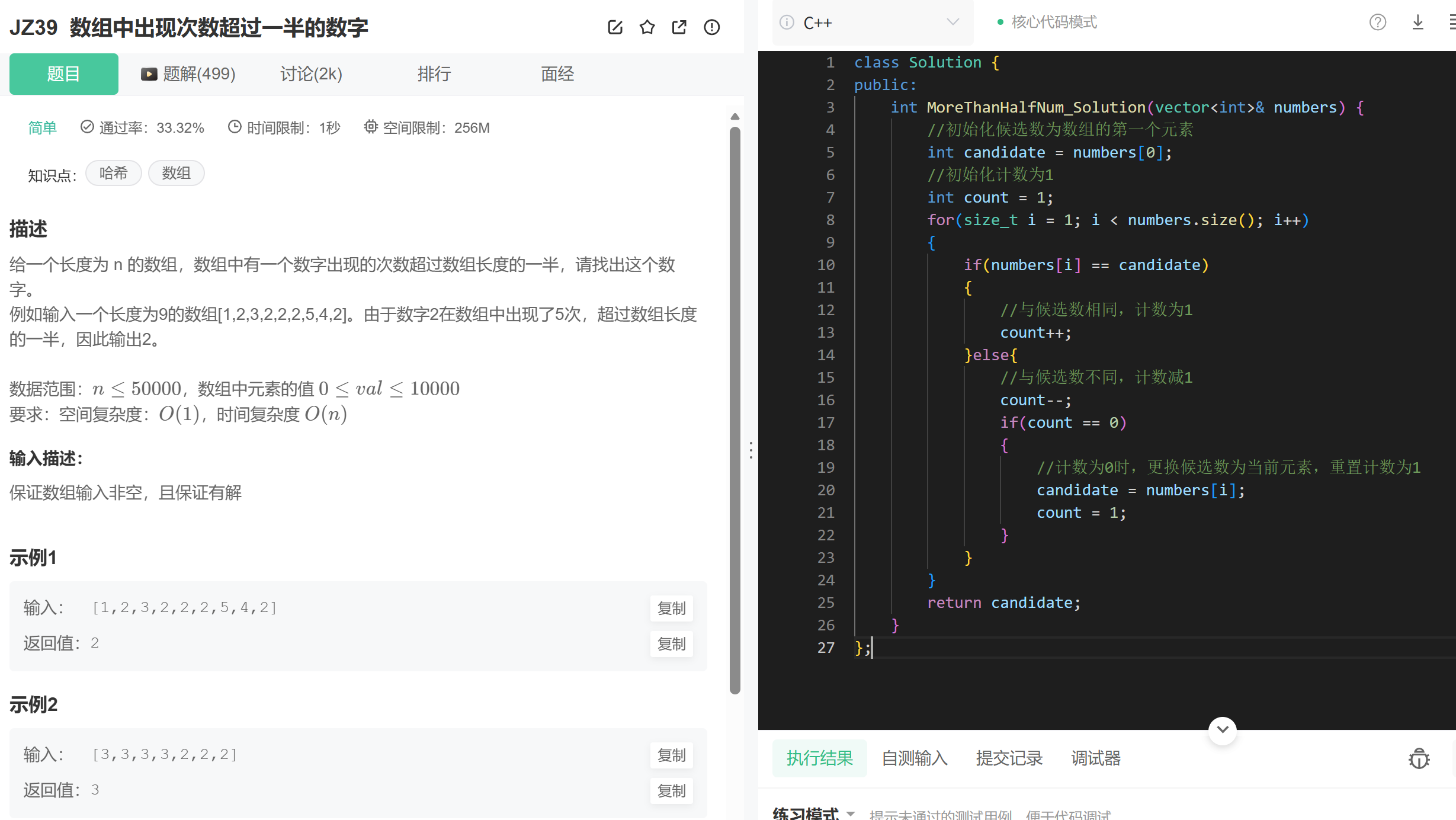
思路分析
摩尔投票法的核心思想是:
- 维护一个候选数和一个计数变量。
- 遍历数组时,若当前元素与候选数相同,计数加 1;否则计数减 1。
- 当计数为 0 时,将当前元素更新为新的候选数,并重置计数为 1。
- 由于目标数字出现次数超过数组长度的一半,最终候选数必然是该目标数字。
样例输入:
假设输入数组为 [1, 2, 3, 2, 2, 2, 5],目标是找到出现次数超过数组长度一半的数字(数组长度为 7,超过一半即至少出现 4 次)。
执行步骤拆解
- 初始化:候选数 candidate 初始化为数组第一个元素 1,计数 count 初始化为 1。(此时状态:candidate=1,count=1)
- 遍历第 2 个元素(值为 2):当前元素 2 与候选数 1 不同,因此 count 减 1,变为 0。
由于 count=0,需要更换候选数为当前元素 2,并重置 count=1。(此时状态:candidate=2,count=1) - 遍历第 3 个元素(值为 3):当前元素 3 与候选数 2 不同,count 减 1,变为 0。
更换候选数为 3,重置 count=1。(此时状态:candidate=3,count=1) - 遍历第 4 个元素(值为 2):当前元素 2 与候选数 3 不同,count 减 1,变为 0。
更换候选数为 2,重置 count=1。(此时状态:candidate=2,count=1) - 遍历第 5 个元素(值为 2):当前元素 2 与候选数 2 相同,count 加 1,变为 2。(此时状态:candidate=2,count=2)
- 遍历第 6 个元素(值为 2):当前元素 2 与候选数 2 相同,count 加 1,变为 3。(此时状态:candidate=2,count=3)
- 遍历第 7 个元素(值为 5):当前元素 5 与候选数 2 不同,count 减 1,变为 2。(此时状态:candidate=2,count=2)
结果分析
遍历结束后,候选数为 2。在原数组中,2 共出现 4 次,确实超过数组长度(7)的一半(3.5),因此结果正确。
这里最重要的原理就是:
目标数字出现次数超过数组长度的一半,意味着它与其他所有数字的总出现次数相比,至少多 1 次。在遍历过程中,目标数字会 "抵消" 掉所有不同的数字,最终剩余的候选数必然是它。
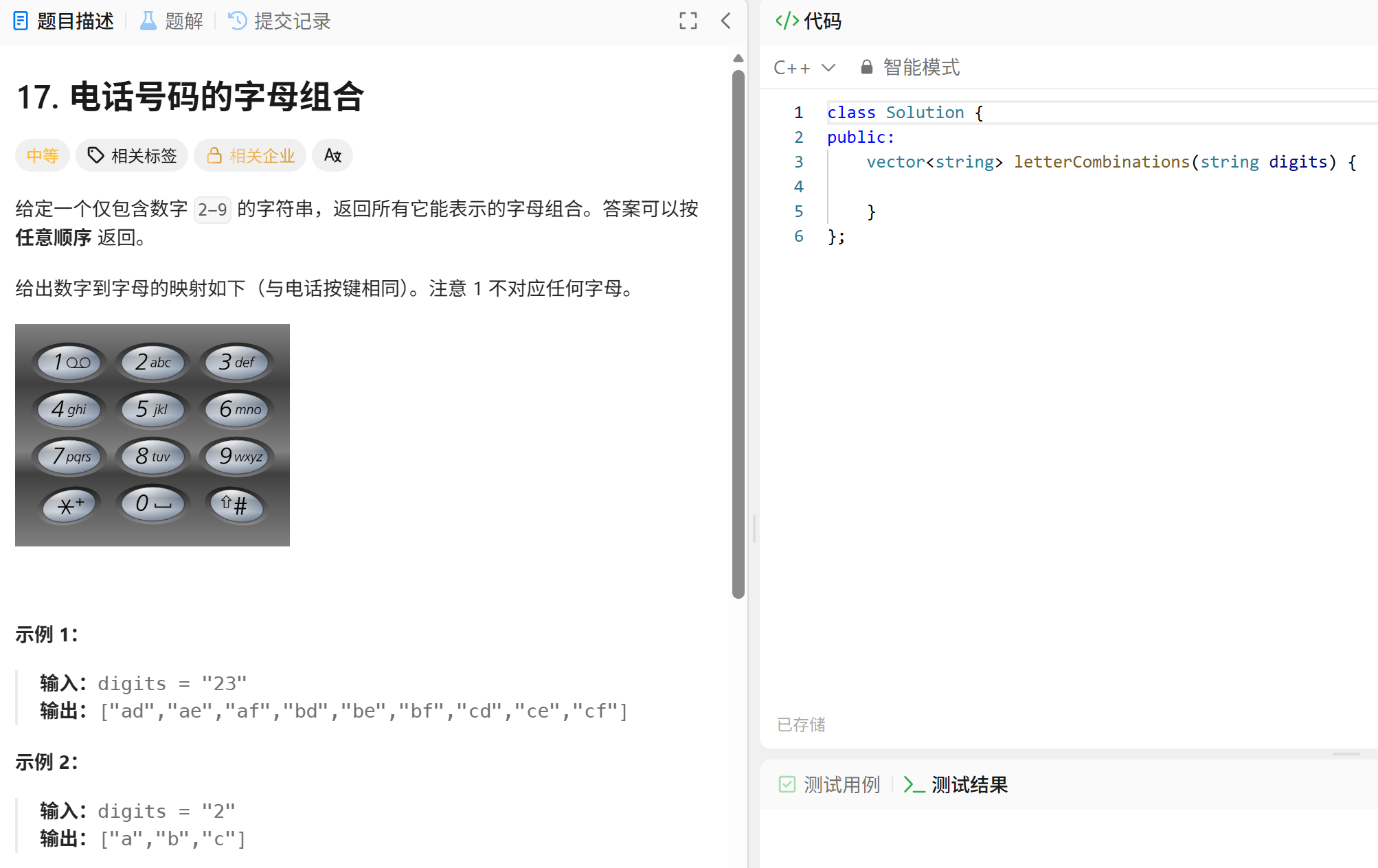
六、电话号码的字母组合
电话号码的字母组合
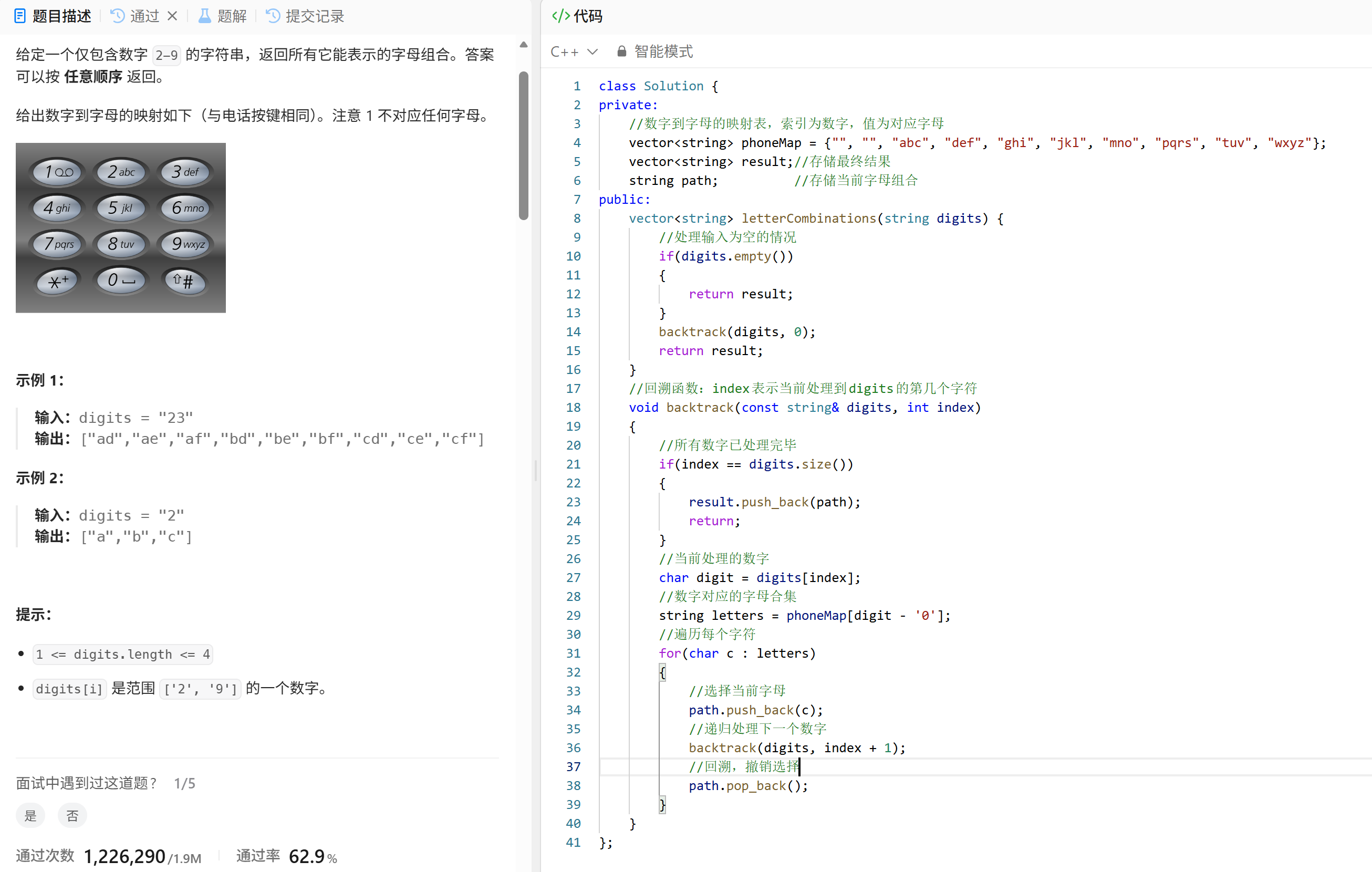
二、解题思路
- 建立映射关系:将每个数字对应的字母存储在一个映射表中,例如用数组 phoneMap 表示,其中 phoneMap[2] = "abc",phoneMap[3] = "def" 等。
- 回溯算法:通过递归尝试每个数字对应的所有字母,生成所有可能的组合。具体步骤:
-
- 维护一个当前组合字符串 path,记录当前已选择的字母。
-
- 维护一个索引 index,表示当前处理到第几个数字。
-
- 当 index 等于输入字符串 digits 的长度时,说明所有数字已处理完毕,将 path 加入结果集。
-
- 否则,取出当前数字对应的所有字母,遍历每个字母,将其加入 path 后递归处理下一个数字(index+1),处理完成后回溯(即删除最后加入的字母)。
下面重点说一下这道题目的核心"回溯算法"
- 什么是回溯算法?
回溯算法本质上是一种 暴力搜索,但它有一个非常聪明的 "回撤" 机制。想象你在走一个迷宫:
-
- 你沿着一条路往前走。
-
- 走着走着,发现这条路是死胡同。
-
- 你需要 退回到上一个路口 ,选择另一条路继续探索。
这个 "退回上一个路口" 的动作,就是 回溯。
- 你需要 退回到上一个路口 ,选择另一条路继续探索。
在编程中,回溯算法通常用 递归 来实现。它非常适合解决需要生成所有可能组合、排列的问题,比如:
- 电话号码的字母组合
- 括号生成
- 全排列
- 子集
- N 皇后问题
- 问题分析(电话号码的字母组合)
给定一个数字字符串,例如 "23",每个数字对应一组字母,我们需要生成所有可能的字母组合。
- 数字 2 对应 "abc"
- 数字 3 对应 "def"
所以,"23" 的所有组合是:ad, ae, af, bd, be, bf, cd, ce, cf
核心思想:我们需要为每个数字选择一个字母,然后将这些字母组合起来。但问题是,数字的长度可能不固定(例如输入可能是 "234"、"2" 等),所以我们需要一种灵活的方式来处理这种动态的选择过程。
- 回溯算法在本题中的应用
我们可以把这个问题看作是一个 决策树 的遍历过程。以输入 "23" 为例,决策树如下:
cpp
(空)
/ | \
a b c (选择数字2的字母)
/|\ /|\ /|\
d e f d e f d e f (选择数字3的字母)
/ | \ ... ... ...
ad ae af ... ... cf (最终组合)回溯算法的执行步骤:
- 选择:从当前数字对应的字母中选择一个。
- 递归:处理下一个数字。
- 撤销选择:回到上一步,选择其他字母。
- 代码分步讲解
概念铺垫
什么是 pop_back()
pop_back() 是 C++ 中 string 和 vector 的成员函数,作用是 删除最后一个元素。
cpp
string s = "abc";
s.pop_back(); // 现在 s 变成 "ab"
s.pop_back(); // 现在 s 变成 "a"
s.pop_back(); // 现在 s 变成空字符串为什么需要 pop_back()
在回溯算法中,我们需要:
- 选择一个字母加入当前组合 path
- 递归处理下一个数字
- 撤销选择,把之前加入的字母从 path 中删掉,以便尝试其他字母
pop_back() 就是用来 撤销选择 的关键操作。
回溯算法执行流程(以 "23" 为例)
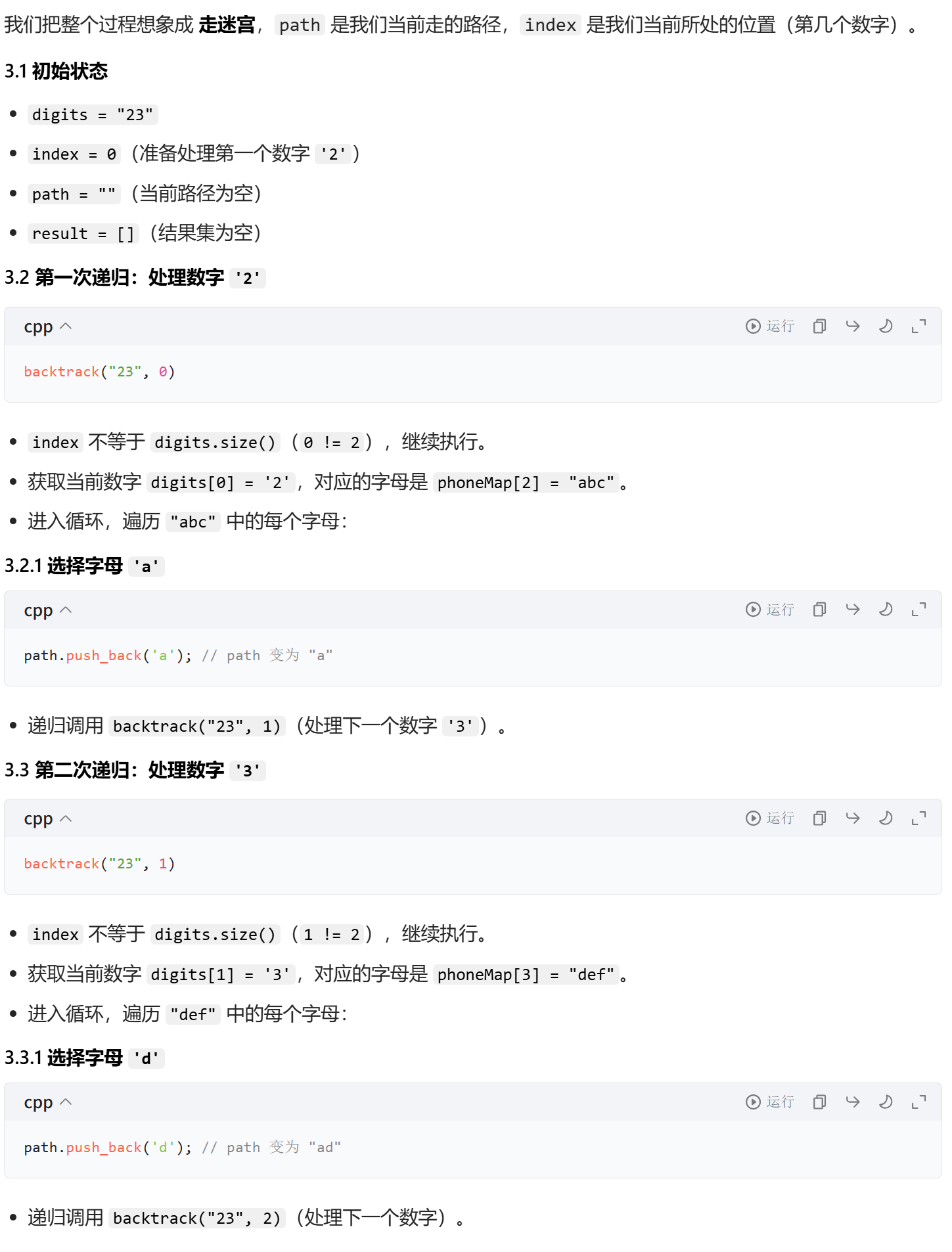
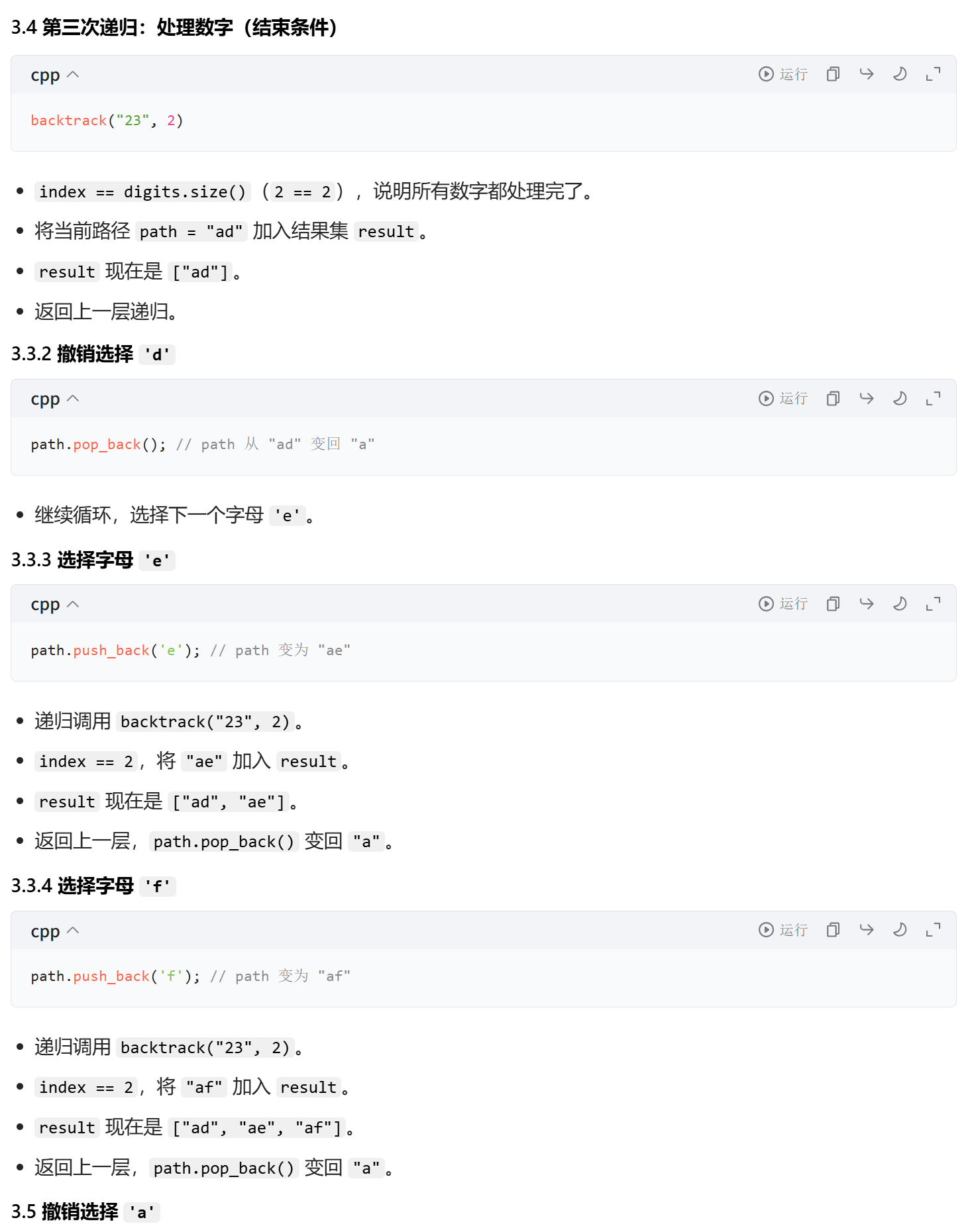
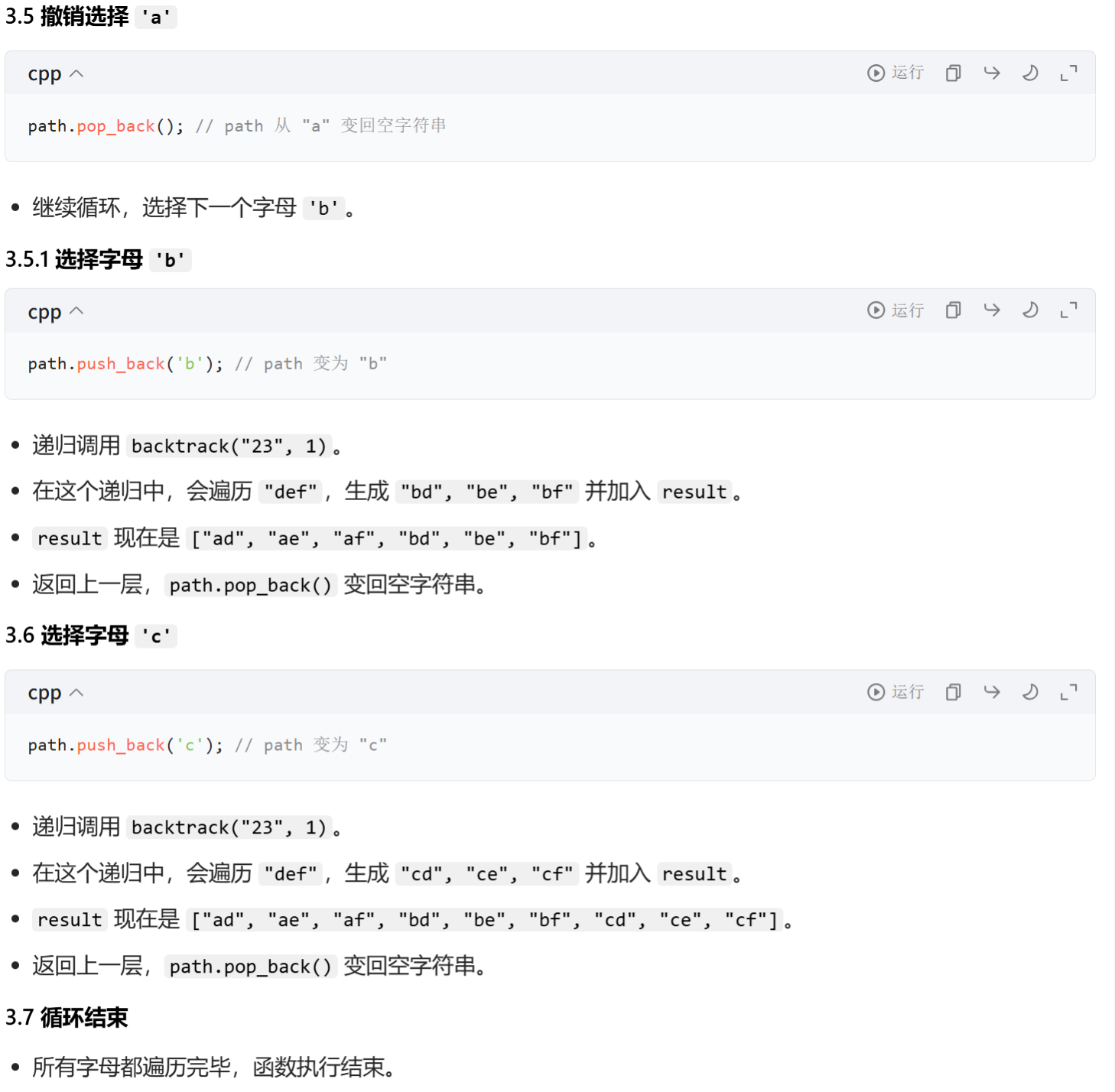
cpp
class Solution {
private:
//数字到字母的映射表,索引为数字,值为对应字母
vector<string> phoneMap = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
vector<string> result;//存储最终结果
string path; //存储当前字母组合
public:
vector<string> letterCombinations(string digits) {
//处理输入为空的情况
if(digits.empty())
{
return result;
}
backtrack(digits, 0);
return result;
}
//回溯函数:index表示当前处理到digits的第几个字符
void backtrack(const string& digits, int index)
{
//所有数字已处理完毕
if(index == digits.size())
{
result.push_back(path);
return;
}
//当前处理的数字
char digit = digits[index];
//数字对应的字母合集
string letters = phoneMap[digit - '0'];
//遍历每个字符
for(char c : letters)
{
//选择当前字母
path.push_back(c);
//递归处理下一个数字
backtrack(digits, index + 1);
//回溯,撤销选择
path.pop_back();
}
}
};结语