hot100-60子集 - 技术栈

一、题目

给定一个整数数组nums，数组中的元素互不相同，返回该数组所有可能的子集。解集不能包含重复的子集，可以

按任意顺序返回。

二、思路

1、使用回溯算法，按顺序枚举每个元素"选"或"不选"的所有可能组合，通过控制起始下标 start 避免重复，每进入一次递归就将当前路径加入结果，从而生成所有子集。

三、代码

java 复制代码

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        backtrack(nums,0,path,res);
        return res;
    }
    public void backtrack(int[] nums,int start,List<Integer> path,List<List<Integer>> res){
        res.add(new ArrayList<>(path));
        for(int i = start; i< nums.length;i++){
            path.add(nums[i]);
            backtrack(nums,i+1,path,res);
            path.remove(path.size()-1);
        }
    }
}

四、举例

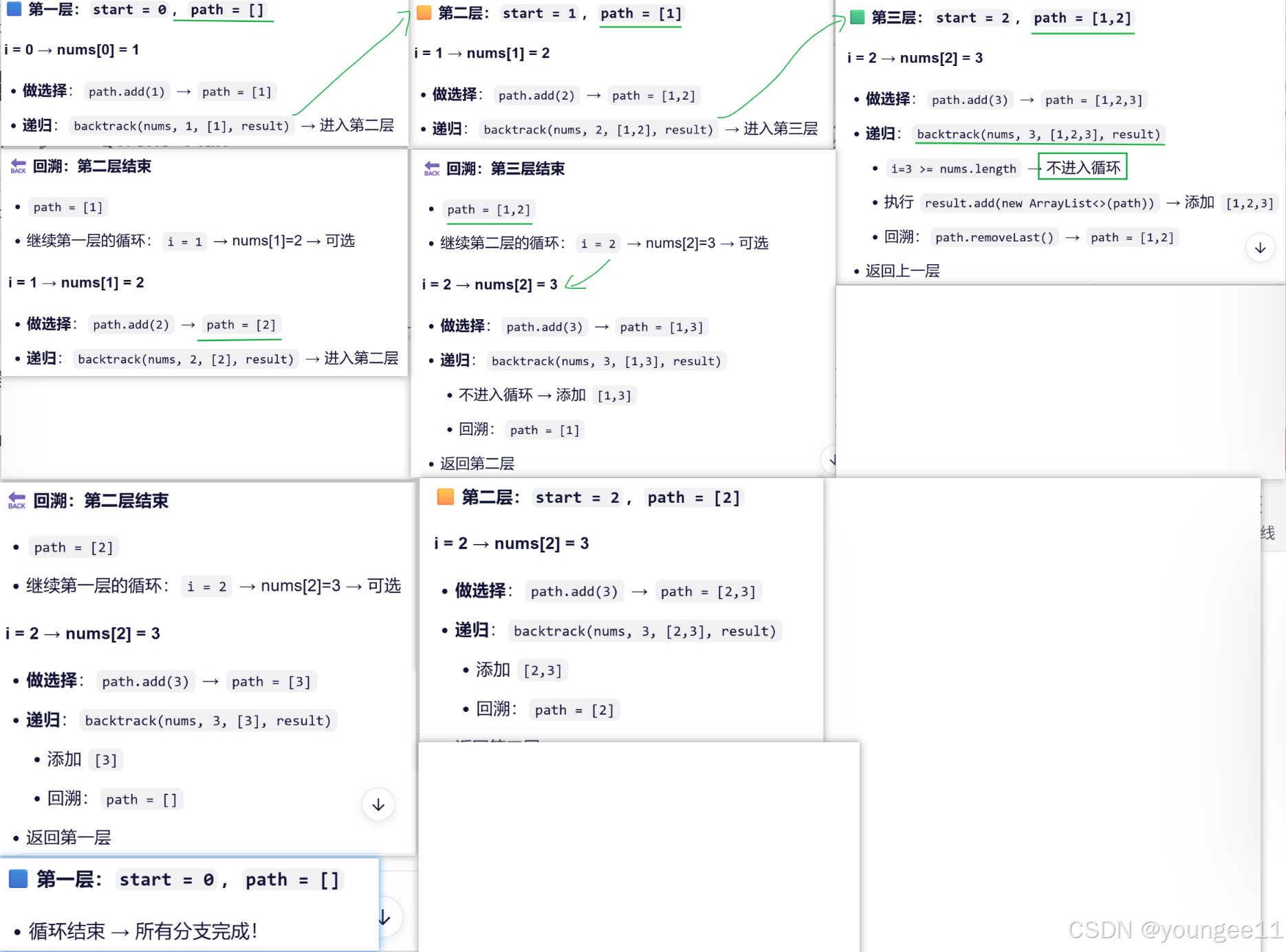
【全排列 vs 子集】

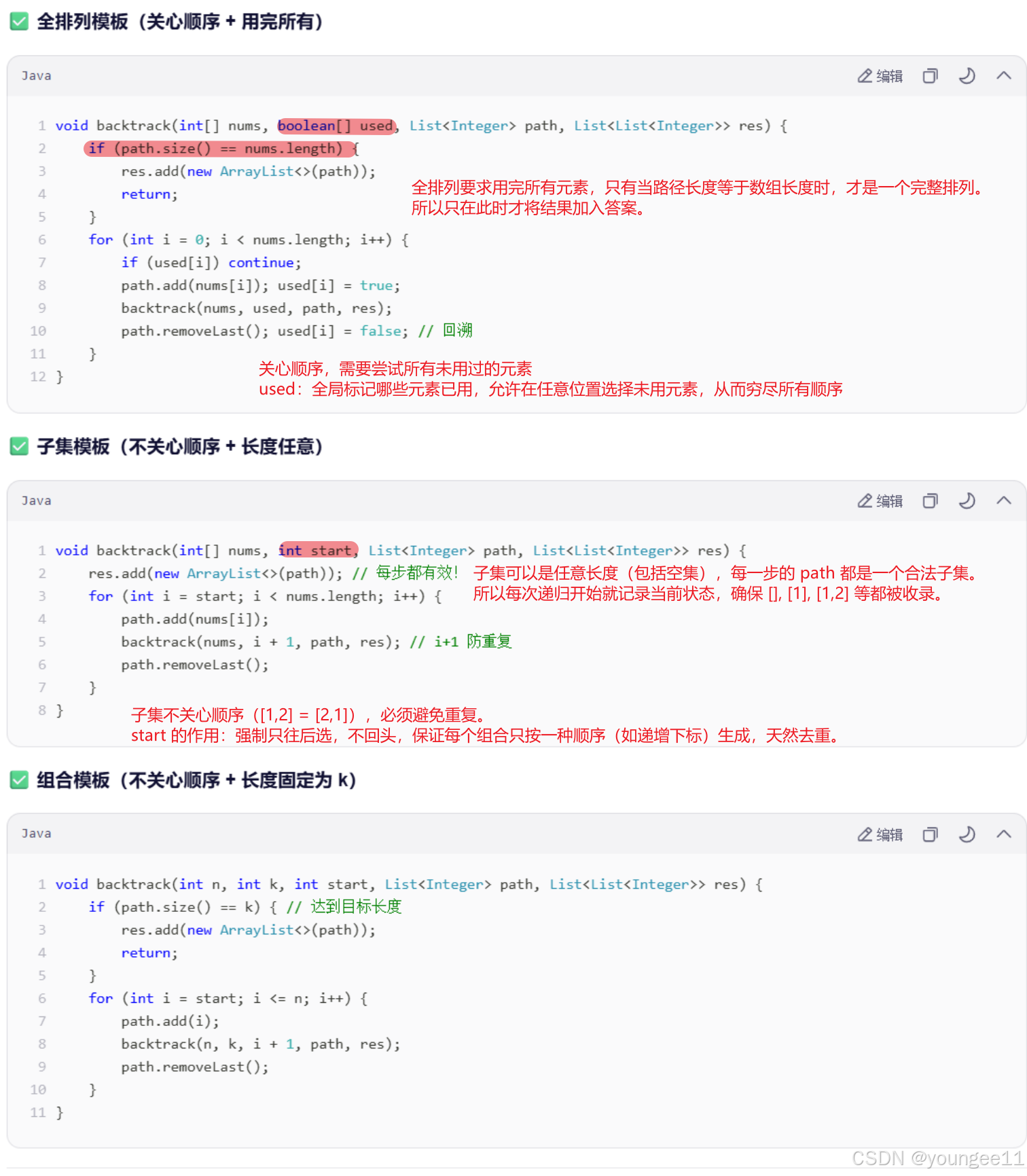
1）子集无序**→ 用 start**

原因：子集不关心顺序（[1,2] = [2,1]），必须避免重复。
start 的作用：强制只往后选，不回头，保证每个组合只按一种顺序（如递增下标）生成，天然去重。

2）全排列有序 → 用 used

原因：排列关心顺序（[1,2] ≠ [2,1]），需要尝试所有未用过的元素，无论位置。
used 的作用：全局标记哪些元素已用，允许在任意位置选择任意未用元素，从而穷尽所有顺序。

3）全排列有终止条件（path.size() == n）

原因：全排列要求用完所有元素，只有当路径长度等于数组长度时，才是一个完整排列。
所以只在此时才将结果加入答案。

4）子集"一进入就加元素"

原因：子集可以是任意长度（包括空集），每一步的 path 都是一个合法子集。
所以每次递归开始就记录当前状态，确保 [], [1], [1,2] 等都被收录。