本文较长,建议点赞收藏。更多AI大模型应用开发学习视频及资料,在智泊AI。
上一篇我们梳理了大模型的基本脉络,并制定了学习计划:阶段一提到数学知识是理解大模型原理的必备内功,因此本章主要回顾下大学和研究生期间线性代数、概率论、微积分、信息论相关的数学知识。本文主要回答几个问题:
1)why:为什么需要学习数学知识?
2)what:大模型和哪些数学知识相关?
3)how:如何学习这些数学知识?
如您对上面问题感兴趣,欢迎关注,学习讨论。
1.为什么需要数学知识?why
许多工程师可能问:既然现在有这么多高级框架(TensorFlow, PyTorch),API调用那么简单,各种成熟模型唾手可得,看起来和做工程没啥太大区别,我为什么还需要去啃那些艰深的数学理论知识?其实本质上取决于你到底是想成为仅仅会使用大模型的"技工",还是希望掌握大模型工作原理及模型优化方案,成为解决复杂场景问题的AI专家。
不知你是否困惑:阅读了无数介绍transformer原理的博客视频依然一头雾水:transformer原理、自注意力工作机制是怎样?Q、K、V三个矩阵作用是怎样的?深度理解数学理论,你将从一个仅仅能"使用"工具的"技工"工程师,升级为能够"创造"、"优化"和"解决复杂问题"的"专家",让你从被动的工具使用者,变为主动的问题解决者和技术创造者。数学理论是AI大模型最根本、最强大的"解决问题的语言",这是在AI领域保持长期竞争力的关键。
| 工程师级别 | 对数学的依赖 | 能力范围 |
| 初级/应用型 | 低:会调用 API,使用现成模型进行微调。 | 解决标准问题,高度依赖现有生态。 |
| 中级/优化型 | 中:理解核心概念,能进行有效调试和部署优化。 | 解决大多数工业问题,是团队的中坚力量。 |
| 高级/专家型 | 高:深度理解原理,能设计新结构,解决复杂、新颖问题。 | 技术领导者,能够定义方向、攻克瓶颈、打造核心竞争力。 |
对于工程师而言,理解AI大模型背后的数学绝非学术炫耀,而是实实在在的生产力、竞争力和职业生涯的护城河。对工程师来说,数学理论不是终点,而是通往更高阶工程能力的"桥梁"。以下是具体原因:
1)问题诊断与调试:从"猜谜"到"精准手术",当模型效果不佳、出现诡异行为或训练失败时,不理解数学的工程师只能进行"盲调"。
➢ 不懂数学的调试:盲目调整超参数(如学习率)、尝试不同的优化器、盲目增加数据或层数。这个过程效率极低,如同在黑暗中摸索,严重依赖经验和运气。
➢ 懂数学的调试:能够根据问题的数学本质,提出假设并精准地验证和修复,极大缩短调试周期,提高开发效率。看到损失曲线不下降,能立刻联想到可能是梯度消失(导数链式法则中断)、学习率过高(梯度下降原理)或数据输入有问题。遇到模型过拟合,能深刻理解 Dropout、权重衰减(L2正则化)为何能 work,而不是仅仅把它们当作一个神奇的"开关"。
2)优化与效率:降低成本,提升性能。大模型的训练和部署成本极其高昂。数学知识是进行优化的根本。
➢ 计算优化:理解矩阵运算(线性代数)和自动微分(微积分)的原理,可以帮助你写出更高效、硬件利用率更高的代码,如优化张量操作、利用广播机制等。
➢ 模型压缩与量化:要将大模型部署到边缘设备,需要进行剪枝、知识蒸馏、量化等技术。这些技术的背后是概率论、信息论和优化理论。例如:剪枝为什么不能简单地剪掉权重小的参数?因为需要理解海森矩阵及其在损失函数中的意义(二阶优化)。量化的本质是在保持数据分布(概率论)的同时减少信息熵(信息论)。
➢ 资源管理:理解训练过程中的内存占用(主要是模型参数和激活函数的中间结果,即张量),能更好地进行批次管理、模型并行和数据并行策略的选择。
3)适配与创新:解决前所未见的问题,数学是你的设计工具箱。它赋予了你打破"拿来主义"、创造性地解决全新问题的能力。
➢ 定制化模型结构:当你需要为一个特定任务(如处理图结构数据、时间序列数据)修改或设计一个新的模型模块时,你必须深刻理解注意力机制(缩放点积、QKV变换)、循环网络(梯度流设计)等背后的数学,才能确保你的设计是有效的、可训练的。
➢ 领域适配:在医疗、金融、科学计算等领域,数据模式和损失函数可能非常特殊。你需要根据领域知识设计合适的损失函数(需要概率论和微积分)和评估指标,而不是简单地调用交叉熵损失。
2.哪些数学理论与AI相关?what
前篇工程师学AI之起始篇:理论与实践学习计划提到大模型的原理建立在三大数学基础之上:线性代数、微积分和概率论。线性代数处理数据表示(线性代数首先将你的文字等多模态信息转化为向量),微积分优化模型参数(微积分通过前向传播和反向传播处理这些向量),概率论与信息论提供理论解释和评估标准(概率论决定最可能的回复),三者缺一不可。

让我们用一个比喻来总结:
1)线性代数是乐高积木:它提供了构建模型的基本模块(向量、矩阵)和组装方式(矩阵乘法)。
2)微积分是说明书和修正工具:它告诉我们当前搭建的模型哪里不好(计算梯度),以及如何调整积木的位置来让它变得更好(梯度下降)。
3)概率论与信息论是设计理念和评估标准:它决定了模型应该学习什么样的模式(数据分布),以及如何衡量模型输出的好坏(交叉熵、困惑度)。
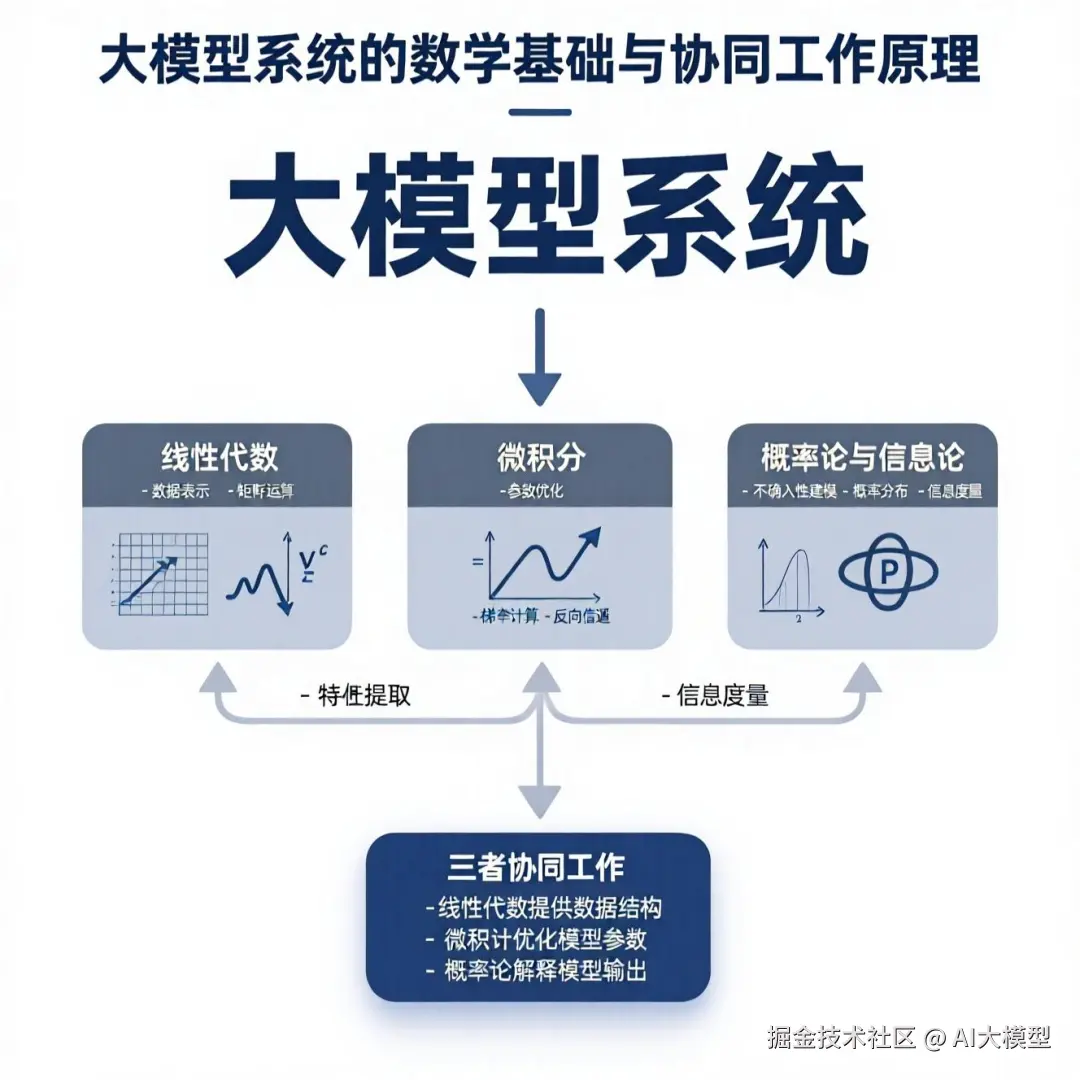
2.1 线性代数:大模型的数据表示(向量/矩阵运算)
线性代数是处理高维数据和并行计算的语言,AI大模型本质上是在高维空间中进行各种变换和运算。
2.1.1基本概念
线性代数基本概念:标量、向量、矩阵、张量:
1)标量:一个数字,比如一个神经元的偏置(Bias)。
2)向量:一维数组,比如一个词的词向量(Word Embedding)或一个神经元的所有输入。
3)矩阵:二维数组,比如一层神经网络的所有权重(Weights)。
4)张量:多维数组(通常三维及以上),是向量和矩阵的推广。整个神经网络的输入、输出和参数都可以用张量表示。例如,一个批次的图像数据是 [batch_size, height, width, channels] 的4维张量。
2.1.2核心运算
1)矩阵乘法:这是神经网络前向传播的核心。一层的输出是输出 = 激活函数(输入 × 权重矩阵 + 偏置)。矩阵乘法高效地实现了所有神经元输入的加权求和。
2)点积:点积运算在自注意力机制(SelfAttention)中至关重要。查询(Query)向量和键(Key)向量之间的点积计算了它们的相似度。
2.1.3线性代数:大模型的数据表达与运算语言
线性代数是大模型最直接、最表象的数学语言。整个模型本质上就是一系列复杂的线性代数运算:高维向量和矩阵运算。简单比喻:线性代数提供了如何用"数字块"(向量和矩阵)"来表示和操作"概念"的基本语法。
1)词嵌入 (Word Embedding):模型中的每个词(Token)都被表示成一个高维向量(一串数字)。这个向量空间中的几何关系(如距离、方向)编码了词语的语义和语法关系。例如,"国王" - "男人" + "女人" ≈ "女王"。
2)模型本身就是巨大的矩阵:神经网络每一层的权重(Weights)和偏置(Biases)都是巨大的矩阵。模型的训练过程就是在调整这些矩阵中的数值。
3)前向传播就是矩阵计算:数据在网络中的传递,本质上就是输入向量与权重矩阵进行矩阵乘法,然后加上偏置,再通过一个激活函数(如ReLU)。
输出 = Activation(权重 · 输入 + 偏置)。
4)注意力机制 (Attention):Transformer的核心-自注意力机制,完全由查询(Query)、键(Key)、值(Value)三个矩阵的运算构成(计算过程涉及矩阵乘法和Softmax)。详细解读欢迎关注,见下一篇文章。
2.2微积分:优化模型参数(损失函数/梯度)
2.2.1基本概念
微积分是模型如何从数据中"学习"的理论基础。它的核心任务是回答:如何调整模型参数,才能让它表现得更好?
1)导数:衡量函数输出随输入变化的瞬时速率。在一元函数中,是斜率。
2)梯度:多元函数的导数推广。它是一个向量,指向函数值增长最快的方向。在机器学习中,损失函数 L(θ) 的梯度 ∇L(θ) 指向了损失增长最快的方向。
3)链式法则:神经网络是深度复合函数(L(g(f(x))))。链式法则允许我们将损失函数对最底层参数的导数,一层一层地反向传播回去。这是反向传播算法的核心。
4)梯度下降:核心思想:既然梯度指向损失增长的方向,那么它的反方向 -∇L(θ) 就是损失下降最快的方向。更新规则:θ_new = θ_old - learning_rate * ∇L(θ_old)通过不断沿负梯度方向微小地更新参数 θ,损失函数的值会逐渐减小,模型性能逐步提升。
5)在大模型中的应用:整个训练过程就是基于梯度下降及其变体(如Adam、AdaGrad)来优化数百万甚至万亿级的参数,最小化预测损失。
篇幅原因这里暂不展开介绍,后面单独章节学习微积分与大模型的关系。
2.2.2微积分:大模型"优化引擎"
微积分是让大模型能够学习的关键,它指导模型如何从错误中改进。核心关系:梯度下降与优化
1)反向传播 (Backpropagation):这是模型学习的核心算法。它通过链式法则,从输出层反向计算损失函数对于网络中每一个参数的梯度。梯度是一个向量,指向损失函数增长最快的方向。
2)梯度下降 (Gradient Descent):优化算法(如Adam)利用计算出的梯度,沿着梯度相反的方向(即损失下降最快的方向)微调所有参数(那些矩阵中的数),从而逐步降低损失,使模型预测更准确。
简单比喻:微积分提供了"如何调整模型内部旋钮(参数)才能让它表现得更好"的精确指导手册。
2.3概率论与信息论:模型评估标准与"决策依据"
概率论为AI提供了在不确定性下进行推理的框架,而信息论则提供了衡量信息的方法。篇幅原因后面章节再进行详细拆解概率论基础知识及其在大模型中的应用。
2.3.1概率论
1)基本概念:概率分布、条件概率、贝叶斯定理。
2)极大似然估计:很多模型的训练目标可以解释为"找到一组参数,使得观测到的数据出现的概率(似然度)最大"。交叉熵损失函数就源于MLE。
3)生成模型:像GPT这样的自回归模型,其本质是学习一个数据分布 P(x)。它每次预测下一个词,就是在计算条件概率分布 P(下一个词 | 已生成的上文)。
2.3.2信息论
1)熵:衡量一个随机变量的不确定性。熵越大,不确定性越大。
2)交叉熵:衡量两个概率分布 P (真实分布) 和 Q (模型预测分布) 之间的差异。它是最常用的损失函数。当 P 和 Q 完全相同时,交叉熵最小。
3)KL散度:衡量两个分布之间的差异程度,与交叉熵紧密相关。
2.3.3概率论:模型思考与决策
大模型本质上是一个概率生成模型,它总是在计算"什么最有可能出现"。概率论决定了大模型的思维方式(概率分布与统计)和最终目标,概率论决定了模型如何"思考"和"决策"
1)训练目标:预训练的核心任务是自监督学习,即根据上文预测下一个词的概率分布。P(下一个词 | 上文),这完全是一个概率问题。
2)损失函数:语言模型普遍使用交叉熵损失来衡量"预测的概率分布"与"真实的one-hot分布"(实际的下一个词)之间的差距。
损失函数与概率论及微积分关系:概率论决定了损失函数"是什么"(它的形式和目的),而微积分决定了我们"如何优化"它(找到使其最小化的方法)。用类比来解释这种关系:1)概率论是"立法者",它制定了法律(损失函数),定义了什么是"好"(低损失)和"坏"(高损失)。2)微积分是"执法者"或"工程师",它提供了工具(梯度下降)来尽可能地达到"好"的状态(最小化损失)。3)生成与采样:模型输出一个词汇表上的概率分布,通过采样(如Top-p采样)来选择下一个词,从而生成文本。生成就是基于概率采样:当你让模型生成文本时,它计算出词汇表中所有词的概率分布,然后根据某种策略(如贪心搜索、核采样)从这个分布中采样下一个词。这引入了随机性和创造性。
4)涌现能力:思维链 (Chain-of-Thought)等技术可以看作是在引导模型生成一个高概率的、逻辑正确的推理路径。
5)模型评估:困惑度是评估语言模型好坏的关键指标,使用困惑度(Perplexity)等基于概率的指标来衡量模型性能,它本质上是交叉熵的指数形式。困惑度越低,模型对下一个词的预测越确定,性能越好。
3.学习路径:如何学习数学理论?how
《深度学习》里面提到掌握深度学习理论的学习框架也提到数学理论的重要性。如果你想深入理解这些概念和理论,建议按以下顺序学习:
1)线性代数 -> 掌握数据和运算的表示。
2)微积分 -> 掌握核心的学习算法。
3)概率论与信息论 -> 掌握模型的评估和生成原理。
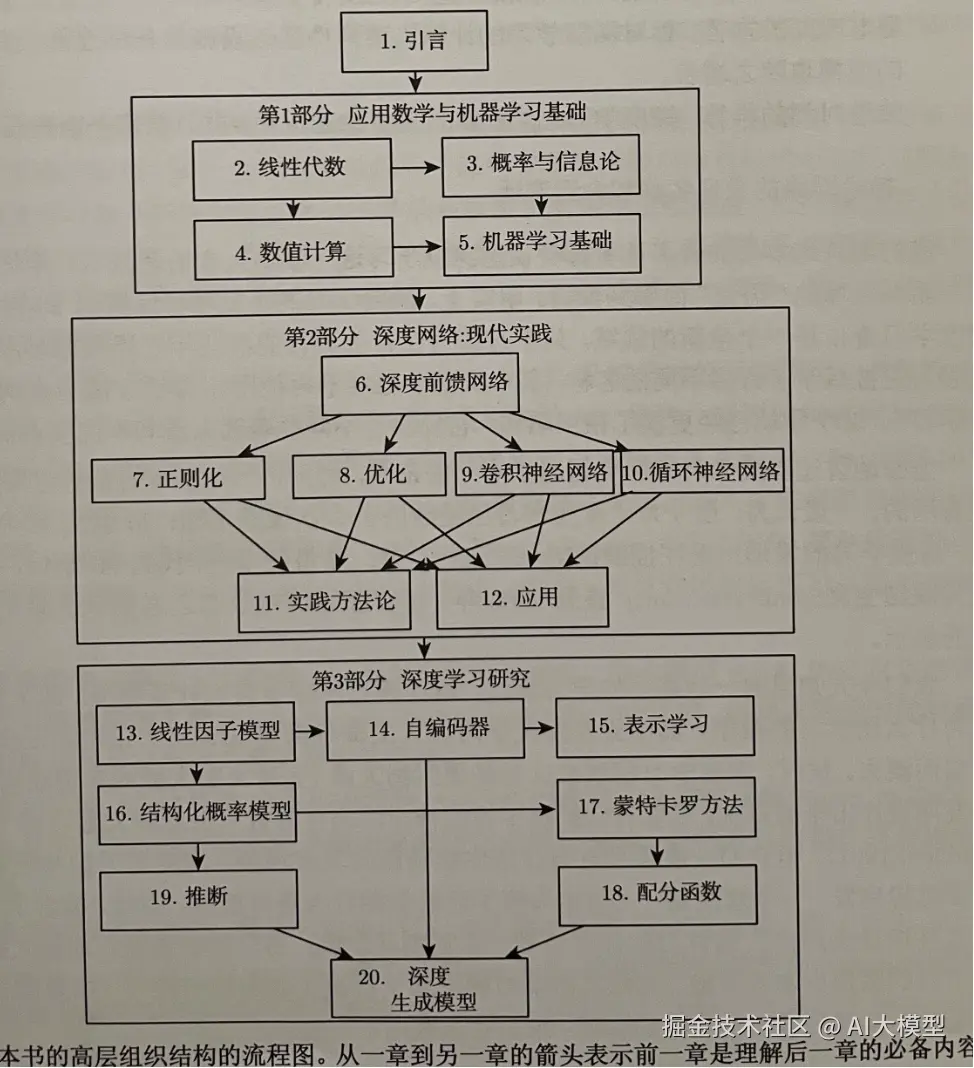
《深度学习》里面提到的数学基础概念如下,我们将拆分为几篇文章来深入学习相关知识及其在大模型中的作用。



最终,这些数学知识并非孤立存在,而是完美地交织在一起,共同赋予了大型语言模型令人惊叹的"智能"。
学习资源推荐
如果你想更深入地学习大模型,以下是一些非常有价值的学习资源,这些资源将帮助你从不同角度学习大模型,提升你的实践能力。
本文较长,建议点赞收藏。更多AI大模型应用开发学习视频及资料,在智泊AI。