pytorch 卷积操作

文章目录

[conv2d 示例](#conv2d 示例)
最大池化
非线性激活
线性层
[Sequential 的使用](#Sequential 的使用)
损失函数
- 神经网络对于损失函数的运用
优化器

conv2d 示例

c 复制代码

import torch
import torch.nn.functional as F

input = torch.tensor([[1, 2, 0, 3, 1],
                      [0, 1, 2, 3, 1],
                      [1, 2, 1, 0, 0],
                      [5, 2, 3, 1, 1],
                      [2, 1, 0, 1, 1]])

kernel = torch.tensor([[1, 2, 1],
                       [0, 1, 0],
                       [2, 1, 0]])


input = torch.reshape(input, (1, 1, 5, 5))  # (1,1,5,5) （1是批量大小 ,1维度，5宽，5高）
kernel = torch.reshape(kernel, (1, 1, 3, 3))

print(input.shape)
print(kernel.shape)

output = F.conv2d(input, kernel, stride=1)
print(output)

output2 = F.conv2d(input, kernel, stride=2)
print(output2)

output3 = F.conv2d(input, kernel, stride=1, padding=1)
print(output3)

最大池化

在保留显著特征的同时，降低数据的空间维度（高度和宽度），从而减少计算量、内存占用，并增强模型的平移不变性。

c 复制代码

import torch
import torchvision
from torch import nn
from torch.nn import MaxPool2d
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter


dataset = torchvision.datasets.CIFAR10(
    "../data", train=False, download=True,
    transform=torchvision.transforms.ToTensor())

dataloader = DataLoader(dataset, batch_size=64)

class Test(nn.Module):
    def __init__(self):
        super().__init__()  # ✅ 关键修复！
        self.maxpool1 = MaxPool2d(kernel_size=3, ceil_mode=False)
    def forward(self, input):
        return self.maxpool1(input)
test = Test()
writer = SummaryWriter("logs_maxpool")
step = 0
for imgs, _ in dataloader:
    writer.add_images("input", imgs, step)
    output = test(imgs)
    writer.add_images("output", output, step)
    step += 1
writer.close()
print("✅ Done! Run: tensorboard --logdir=logs_maxpool")

非线性激活

引入非线性，使神经网络能够拟合任意复杂的函数；如果没有它，多层网络就等价于单层线性模型。

c 复制代码

import torch
import torchvision
from torch import nn
from torch.nn import Sigmoid
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter

# 加载数据集
dataset = torchvision.datasets.CIFAR10(
    "../data",
    train=False,
    download=True,
    transform=torchvision.transforms.ToTensor()
)
dataloader = DataLoader(dataset, batch_size=64)

# 定义模型（修正类名和 forward 缩进）
class Test(nn.Module):  # ✅ 正确继承 nn.Module
    def __init__(self):
        super(Test, self).__init__()
        self.sigmoid1 = Sigmoid()

    def forward(self, x):
        return self.sigmoid1(x)

test = Test()
writer = SummaryWriter("logs_Sigmoid")
step = 0

for data in dataloader:
    imgs, targets = data
    writer.add_images("input", imgs, step)
    output = test(imgs)
    writer.add_images("sigmoid_output", output, step)
    step += 1

writer.close()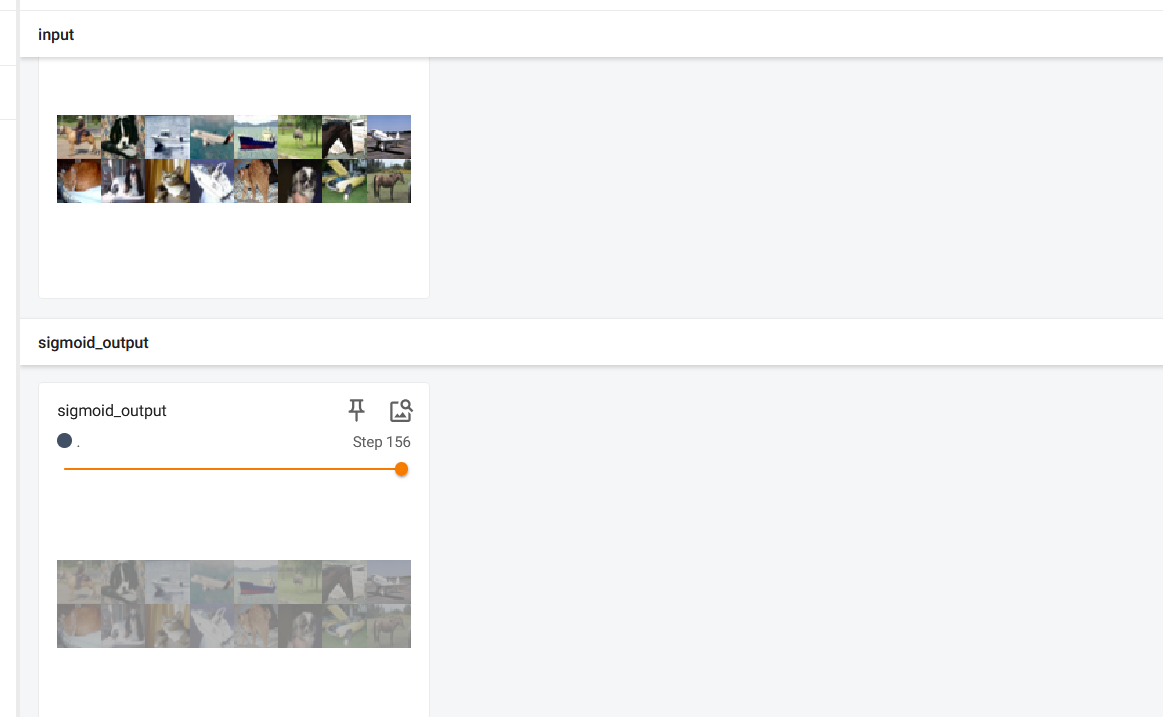

线性层

对输入进行仿射变换（Affine Transformation）：即 output = weight × input + bias，用于学习输入特征到输出空间的映射关系。

c 复制代码

import torch
import torch.nn as nn

# 定义一个线性层：输入维度=784，输出维度=10
linear = nn.Linear(in_features=784, out_features=10)
# 输入：batch=32, 每个样本784维（如展平的28x28图像）
x = torch.randn(32, 784)
# 前向传播
y = linear(x)  # 输出形状: (32, 10)

Sequential 的使用

py 复制代码

import torch
from torch import nn
from torch.nn import Conv2d, MaxPool2d, Flatten, Linear, Sequential
from torch.utils.tensorboard import SummaryWriter


class Test(nn.Module):
    def __init__(self):
        super(Test, self).__init__()
        self.model1 = Sequential(
            Conv2d(3, 32, 5, padding=2),
            MaxPool2d(2),
            Conv2d(32, 32, 5, padding=2),
            MaxPool2d(2),
            Conv2d(32, 64, 5, padding=2),
            MaxPool2d(2),
            Flatten(),
            Linear(1024, 64),
            Linear(64, 10)
        )

    def forward(self, x):
        x = self.model1(x)
        return x

test = Test()
print(test)
input = torch.ones((64, 3, 32, 32))
output = test(input)
print(output.shape)

writer = SummaryWriter("./logs_seq")
writer.add_graph(test, input)
writer.close()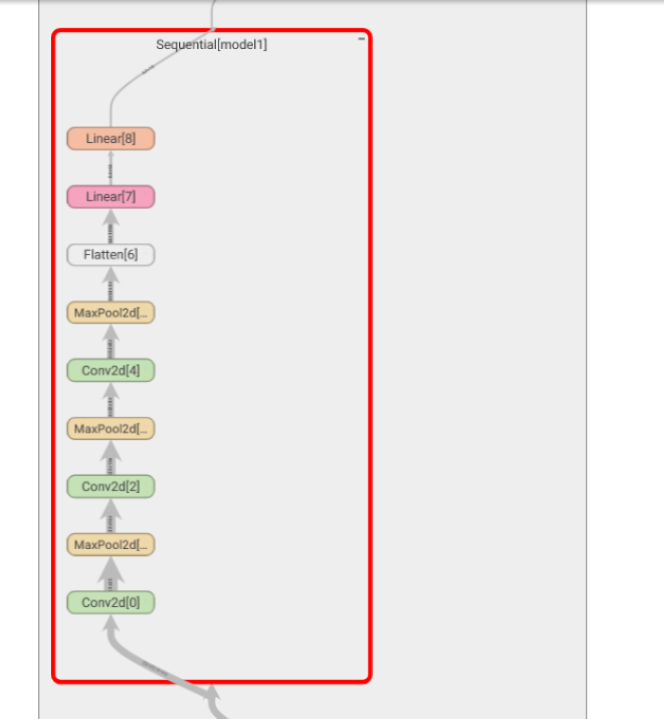

损失函数

L1Loss ------ 平均绝对误差（Mean Absolute Error, MAE）

c 复制代码

inputs = [1, 2, 3]

targets = [1, 2, 5]

# 差值: [0, 0, -2] → 绝对值: [0, 0, 2]

适用场景：

回归任务（如预测房价、温度）

对异常值不敏感（相比 MSE）

MSELoss ------ 均方误差（Mean Squared Error, MSE）

c 复制代码

差值 = [0, 0, -2]

平方 = [0, 0, 4]

平均 = (0 + 0 + 4) / 3 ≈ 1.333...

适用场景：

回归任务（最常用）

对大误差惩罚更重（因为平方），适合希望减少大偏差的场景

CrossEntropyLoss ------ 交叉熵损失（用于分类）

x = torch.tensor([0.1, 0.2, 0.3]) # 1个样本，3个类别的 logits

y = torch.tensor([1]) # 真实类别是第 1 类（索引从0开始）

c 复制代码

# 内部计算：

# 1. Softmax(x) = [e^0.1, e^0.2, e^0.3] / sum ≈ [0.30, 0.33, 0.37]

# 2. 取真实类别（index=1）的概率：0.33

# 3. Loss = -log(0.33) ≈ 1.1019

适用场景：

多分类任务（如 CIFAR-10、ImageNet）

c 复制代码

import torch
from torch.nn import L1Loss
from torch import nn

inputs = torch.tensor([1, 2, 3], dtype=torch.float32)
targets = torch.tensor([1, 2, 5], dtype=torch.float32)

inputs = torch.reshape(inputs, (1, 1, 1, 3))
targets = torch.reshape(targets, (1, 1, 1, 3))

loss = L1Loss(reduction='sum')
result = loss(inputs, targets)

loss_mse = nn.MSELoss()
result_mse = loss_mse(inputs, targets)

print(result)
print(result_mse)


x = torch.tensor([0.1, 0.2, 0.3])
y = torch.tensor([1])
x = torch.reshape(x, (1, 3))
loss_cross = nn.CrossEntropyLoss()
result_cross = loss_cross(x, y)
print(result_cross)

神经网络对于损失函数的运用

c 复制代码

import torch
import torchvision
from torch import nn
from torch.utils.data import DataLoader

dataset = torchvision.datasets.CIFAR10("../data", train=True, transform=torchvision.transforms.ToTensor(), download=True)
dataloader = DataLoader(dataset, batch_size=64)

class Test(nn.Module):
    def __init__(self):
        super().__init__()
        self.model = nn.Sequential(
            nn.Conv2d(3, 32, 5, padding=2),
            nn.ReLU(),
            nn.MaxPool2d(2),
            nn.Conv2d(32, 32, 5, padding=2),
            nn.ReLU(),
            nn.MaxPool2d(2),
            nn.Conv2d(32, 64, 5, padding=2),
            nn.ReLU(),
            nn.MaxPool2d(2),
            nn.Flatten(),
            nn.Linear(64*4*4, 64),
            nn.ReLU(),
            nn.Linear(64, 10)
        )

    def forward(self, x):
        return self.model(x)

model = Test()
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# 训练一步
for imgs, targets in dataloader:
    outputs = model(imgs)
    loss = loss_fn(outputs, targets)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    print(f"Loss: {loss.item():.4f}")
    break

优化器

作用：根据损失函数对模型参数的梯度，自动更新网络权重，使模型逐步逼近最优解。

c 复制代码

import torch
import torch.nn as nn
import torch.optim as optim

# 简单线性模型: y = w * x + b
model = nn.Linear(1, 1)
optimizer = optim.SGD(model.parameters(), lr=0.1)

x = torch.tensor([[2.0]])
y_true = torch.tensor([[5.0]])  # 真实值

print("初始权重:", model.weight.item(), "偏置:", model.bias.item())

for i in range(3):
    optimizer.zero_grad()
    y_pred = model(x)
    loss = (y_pred - y_true) ** 2
    loss.backward()
    optimizer.step()
    print(f"Step {i+1}: loss={loss.item():.4f}, w={model.weight.item():.4f}, b={model.bias.item():.4f}")

c 复制代码

初始权重: 0.4567 偏置: -0.1234
Step 1: loss=16.2345, w=0.8567, b=0.2766
Step 2: loss=9.8765, w=1.2567, b=0.6766
Step 3: loss=5.4321, w=1.6567, b=1.0766
→ 权重和偏置在逐步向真实值（w=2.5, b=0）靠近！