【代码随想录c++刷题】-二分查找 移除元素 有序数组的平方 - 第一章 数组 part 01

目录

• • • • 第一题：二分查找
      • 第二题：移除元素
      • 第三题：有序数组的平方

第一题：二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果 target 存在返回下标，否则返回 -1。

你必须编写一个具有 O(log n) 时间复杂度的算法。


示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
 

提示：

你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

解1，区间左闭右开情况[ )：

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size();
        while(left < right){
            int middle = (left+right)/2;
            if( target < nums[middle]){
                right = middle;
            }
            else if( target > nums[middle]){
                left = middle + 1;
            }
            else{
                return middle;
            }
        }
        return -1;
    }
};

解2，区间左闭右闭情况[ ]：

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // -1
        while(left <= right){
            int middle = (left+right)/2;
            if( target < nums[middle]){
                right = middle - 1; // -1
            }
            else if( target > nums[middle]){
                left = middle + 1;
            }
            else{
                return middle;
            }
        }
        return -1;
    }
};

原因（左闭右闭区间）：
因为 nums[middle] 已经和 target 比较过了 ------ 既然 target < nums[middle]，说明 nums[middle] 肯定不是目标，后续的有效区间绝对不能包含 middle。
而左闭右闭区间的 right 是「包含在区间内的」，如果不把 right 改成 middle-1，而是直接设为 middle，那么下一轮区间还是会包含 middle（比如当前 middle=2，right=2，区间 [left,2] 仍包含 nums[2]），这就重复检查了无效元素，甚至可能导致死循环。
举个例子：nums = [1,3,5]，target=0（比所有元素小）：
初始 left=0，right=2（正确的左闭右闭初始值），middle=1，nums[1]=3>0 → right=1-1=0。
下一轮 left=0，right=0，middle=0，nums[0]=1>0 → right=0-1=-1。
循环结束（left>right），返回 -1，逻辑正确。

左闭右开区间：为什么不需要减 1？
如果换成左闭右开区间 [left, right)，逻辑要整体调整，核心是「right 本身不包含在有效区间内」：

初始 right = nums.size() → 正确（因为 nums[size] 越界，刚好符合「右开」的不包含特性）。

循环条件 left < right → 符合左闭右开：当 left == right 时，[left, right) 是空区间（没有元素），无需检查。

重点：target < nums[middle] 时，right = middle（不需要减 1）。

原因（左闭右开区间）：
同样，nums[middle] 已经确定不是目标，但左闭右开区间的 right 是「不包含在区间内的」。把 right 设为 middle，意味着下一轮的有效区间是 [left, middle)------ 这个区间自然就排除了 nums[middle]（因为 middle 是右边界，不包含），完全符合需求。

举个例子：nums = [1,3,5]，target=0（左闭右开）：
初始 left=0，right=3，middle=1，nums[1]=3>0 → right=1（无需减 1）。
下一轮 left=0，right=1，middle=0，nums[0]=1>0 → right=0。
循环结束（left==right），返回 -1，逻辑正确。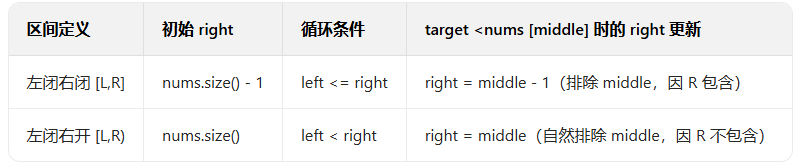

第二题：移除元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。

假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作：

更改 nums 数组，使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
返回 k。

用户评测：
评测机将使用以下代码测试您的解决方案：

int[] nums = [...]; // 输入数组
int val = ...; // 要移除的值
int[] expectedNums = [...]; // 长度正确的预期答案。
                            // 它以不等于 val 的值排序。

int k = removeElement(nums, val); // 调用你的实现

assert k == expectedNums.length;
sort(nums, 0, k); // 排序 nums 的前 k 个元素
for (int i = 0; i < actualLength; i++) {
    assert nums[i] == expectedNums[i];
}
如果所有的断言都通过，你的解决方案将会 通过。

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2,_,_]
解释：你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。
你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。
示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3,_,_,_]
解释：你的函数应该返回 k = 5，并且 nums 中的前五个元素为 0,0,1,3,4。
注意这五个元素可以任意顺序返回。
你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。
 

提示：

0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100

这是两个for循环的暴力解法，时间复杂度：O(n^2)：

这是双指针解法，时间复杂度：O(n)：

利用双指针，fast快指针，去找该放入新的数组的数值。slow慢指针，指向数组开始的下标。

这个for循环控制fast一直走，for循环里条件判断slow是否跟上一起走，妙~

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int fast,slow;
        slow = 0;
        for(fast = 0; fast < nums.size() ; fast++){
            if(nums[fast]!=val){
                nums[slow] = nums[fast];
                slow++;
            }
        }
        return slow;
    }
};

第三题：有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]
示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]
 
提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按 非递减顺序 排序

进阶：

请你设计时间复杂度为 O(n) 的算法解决本问题

这里说的非递减顺序我按递增顺序理解，这里就是两头互相比较，因为这个题肯定是有负数的，所以两头大。如果没有这题用双指针也没啥意义。

这题没看题解之前，也就是注释部分，开始用的push_back()但是要的是升序，所以后面我用的是results.insert(results.begin(),nums[i]*nums[i]);来存入比较获胜的新数组，测下来比用变量k去控制存储到新数组，慢了数倍，尽量不用封装函数。

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        vector<int> results(nums.size(), 0); 
        int k = nums.size()-1;
        for(int i = 0,j = nums.size()-1;i<=j;){
            if(nums[i]*nums[i] > nums[j]*nums[j]){
                //results.insert(results.begin(),nums[i]*nums[i]);
                results[k--] = nums[i] * nums[i];
                i++;
            }else{
               //results.insert(results.begin(),nums[j]*nums[j]);
                results[k--] = nums[j] * nums[j];
                j--;
            }
        }    
        return results;
    }
};