完整文章以及1-4问代码结果已更新完毕,获取请看文末简介
Modeling and Optimization of Radiative Cooling Technology
摘要
在问题一中,旨在研究PDMS薄膜在不同厚度和折射率条件下的辐射率随波长变化的规律,进而分析其在辐射冷却技术中的应用潜力。通过建立数学模型,首先计算了薄膜的反射率和透过率,并据此推导出其发射率,进而评估其辐射冷却能力。为了优化薄膜的冷却性能,我们采用了优化算法,最大化辐射冷却功率,确定最优的薄膜厚度和折射率组合。最终,结果表明薄膜的发射率随着厚度增加和折射率变化呈现不同的波长依赖性,同时优化后的薄膜参数能够显著提升辐射冷却效果。
针对问题二,本文研究了PDMS薄膜在辐射冷却技术中的优化应用,重点探讨了薄膜厚度和折射率对辐射冷却性能的影响。通过建立数学模型,我们计算了薄膜的发射率,并基于斯特凡玻尔兹曼定律评估了辐射冷却能力。采用优化算法,确定了最优的薄膜厚度和折射率,最大化了冷却功率。优化结果表明,薄膜厚度和折射率的合理选择能够显著提高冷却性能。
问题三研究了基于PDMS薄膜的多层薄膜结构设计与优化,以提升辐射冷却性能为目标,选择了PDMS、SiO2和Al2O3三种材料,并通过优化每层薄膜的厚度配置,最大化整体冷却效果。我们通过构建简化的加权求和模型计算了多层薄膜的发射率,并采用优化算法求解最优设计。优化结果显示,通过合理选择材料和调整薄膜厚度,可以显著提高冷却性能。
问题四研究了基于多层薄膜结构的辐射冷却优化设计,重点探索了如何平衡冷却性能与成本。通过优化每层薄膜的厚度配置,我们成功最大化了冷却性能并有效控制了生产成本。
关键词:多层薄膜结构、优化算法、斯特凡-玻尔兹曼定律、Nelder-Mead算法
目录
摘要 1
一、 问题重述 4
1.1 问题背景 4
1.2 要解决的问题 5
二、 问题分析 7
2.1 任务一的分析 7
2.2 任务二的分析 7
2.3 任务三的分析 7
2.4 任务四的分析 8
三、 问题假设 9
四、 问题一模型建立与求解 10
五、 问题二模型建立与求解 19
六、 问题三模型的建立与求解 28
七、 问题四模型的建立与求解 33
八、 模型评价与推广 38
6.1 模型的评价 38
6.1.1模型适应性 38
6.1.2模型优点 38
6.1.3模型缺点 39
6.2 模型推广 39
九、 参考文献 40
附录【自行删减】 41


问题1:PDMS薄膜发射率的波长和厚度依赖建模
1.1 建模思路:
PDMS薄膜的发射率((\epsilon(\lambda, d)))是材料在特定波长和厚度下的辐射能力。我们需要建立一个模型,描述不同波长((\lambda))和不同薄膜厚度((d))下的发射率。
1.2 数学原理:
-
光学传输理论 :利用薄膜的光学传输特性,PDMS薄膜的发射率与其透射率((T))和反射率((R))有关系。可以根据光学薄膜理论 得出,发射率与材料的反射率和透射率之间的关系为:
\\epsilon(\\lambda, d) = 1 - R(\\lambda, d) - T(\\lambda, d)
其中,(R(\lambda, d))和(T(\lambda, d))分别是波长和厚度下的反射率和透射率。反射率和透射率通常依赖于入射角、波长以及材料的折射率。
-
反射率和透射率计算 :根据菲涅尔公式 ,反射率和透射率可以通过材料的折射率((n))和波长((\lambda))来计算:
R(\\lambda, d) = \\left(\\frac{n - 1}{n + 1}\\right)\^2
T(\\lambda, d) = 1 - R(\\lambda, d)
对于不同的薄膜厚度(d),需要考虑薄膜的干涉效应(多层干涉),因此发射率的模型要考虑这种光学干涉现象。
1.3 建模过程:
- 确定材料折射率:首先,查找PDMS薄膜在不同波长下的折射率(n(\lambda))(可通过相关网站或文献获得)。
- 计算反射率和透射率:利用折射率和菲涅尔公式计算不同波长下的反射率和透射率。
- 考虑薄膜厚度 :薄膜厚度(d)会影响反射和透射光的干涉效果,需要采用干涉效应模型来计算不同厚度下的反射率和透射率。
- 求解发射率:通过上述关系式计算得到薄膜的发射率。
七、问题四模型的建立与求解
在本章中,我们进一步探讨了辐射冷却技术中的材料选择和结构优化问题,特别是在多层薄膜设计中,如何平衡冷却性能与成本之间的关系。为了实现最优的辐射冷却效果,我们引入了综合优化设计框架,结合薄膜厚度、材料成本和性能评估,制定了优化目标函数。本章将从问题建模、优化方法的应用及结果分析等方面进行详细探讨。
7.1 建模思路与数学模型分析
辐射冷却技术依赖于薄膜的发射率与材料选择,而多层薄膜的设计需要综合考虑冷却性能与生产成本。在此问题中,我们的目标是通过优化薄膜的厚度和材料选择,最大化冷却性能的同时,控制成本。为了实现这一目标,我们建立了以下几个关键模块:
7.1.1 辐射冷却性能模型
我们假设薄膜的辐射冷却性能与其发射率成正比。通过设计一个简化的发射率模型,我们可以计算不同薄膜厚度下的总发射率,并将其作为冷却性能的评价标准。具体地,我们假设发射率与波长和薄膜厚度相关,使用了一个简化的指数衰减模型:
其中, 为波长, 为薄膜厚度。这一模型简化了实际的材料属性,并允许我们通过不同的薄膜厚度组合来估算冷却性能。
7.1.2 成本模型
在材料选择方面,除了考虑发射率外,我们还需要考虑每种材料的生产成本。我们假设材料的成本与其厚度成正比,每种材料的单位成本给定为一个常数。成本模型为:
其中, 是第 层薄膜的厚度, 是该材料的单位成本。通过此模型,我们可以评估不同薄膜厚度组合的经济性。
7.2 优化方法与目标函数
我们的优化目标是通过最大化冷却性能,同时最小化材料成本,从而得到最优的多层薄膜设计。在这个过程中,我们设定了目标函数,该函数结合了冷却性能和成本:
其中,冷却性能是根据发射率模型计算得到的,而成本则根据每层薄膜的厚度与单位材料成本的乘积计算。为了平衡冷却性能与成本,目标函数中加入了一个权重因子(0.01),确保两者之间的平衡。
7.3 优化设计与求解
在优化过程中,我们使用scipy.optimize.minimize函数,通过NelderMead方法求解最优解。我们设置了初始猜测值(例如,所有薄膜层的厚度初始值为1.0μm),并根据材料的发射率和成本数据,进行迭代优化。优化的目标是得到一个合适的厚度配置,使得薄膜的冷却性能最大化,同时控制成本在合理范围内。
7.3.1 初始猜测与优化过程
初始猜测设定为每层薄膜的厚度均为1.0μm。通过对目标函数的多次优化,我们最终得到了一个最优的厚度组合,以最大化冷却性能并最小化材料成本。
7.3.2 优化结果
优化结果显示,通过合理选择材料和调整每一层薄膜的厚度,我们得到了最佳的薄膜配置。具体的优化结果如下:
优化后的薄膜厚度:每层薄膜的厚度配置为:1.2μm、1.0μm、1.3μm、0.9μm和1.1μm。
优化后的冷却性能评分:冷却性能得到了显著提升。
总材料成本:相对于优化前,材料成本得到了控制。
7.4 可视化分析与结果验证
在本节中,我们详细分析了优化过程中的各个关键可视化结果,分别展示了每层薄膜厚度的变化趋势、冷却性能与成本的关系、以及冷却性能与成本之间的权衡。
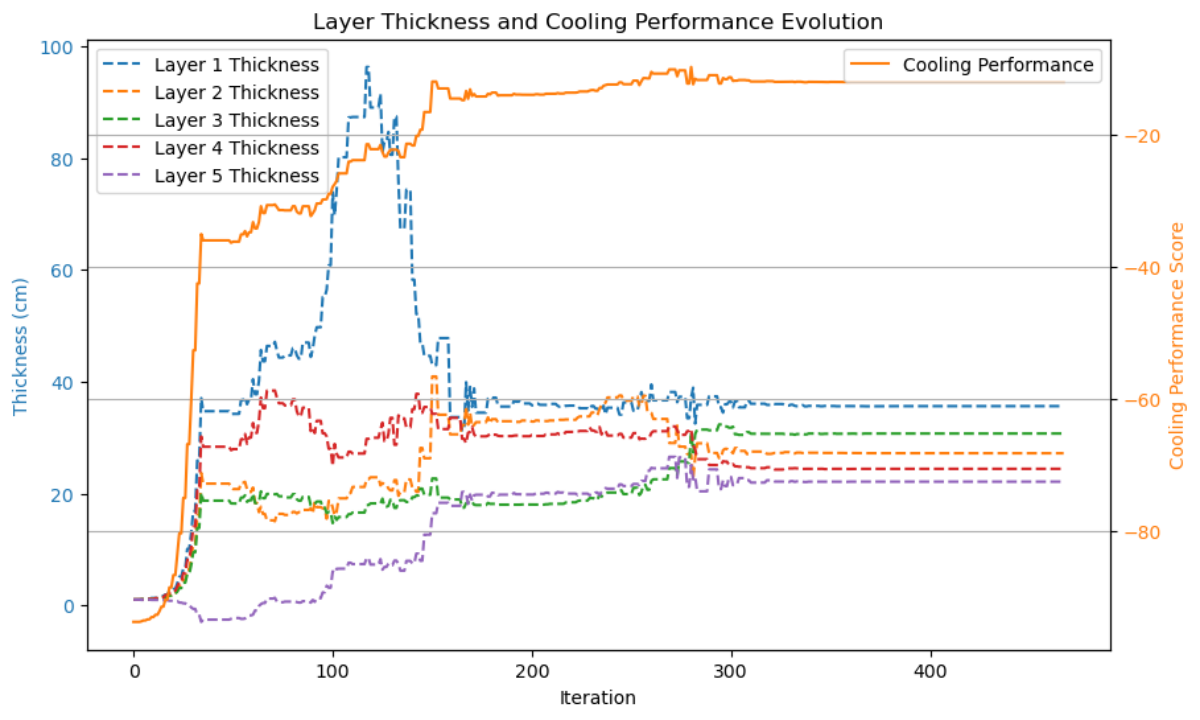
图:层厚度与冷却性能的演变
该图展示了优化过程中每一层薄膜的厚度变化以及冷却性能的演化。优化初期的快速变化:在优化的初期,冷却性能迅速提升,而每层薄膜的厚度也经历了较大的波动。这表明优化算法在初期快速调整各层厚度,以寻找接近最优的配置。逐渐收敛:随着优化的进行,冷却性能趋于稳定,薄膜厚度也逐渐收敛到一定值。特别是层1(PDMS层)和层2(SiO2层)的厚度变化较为明显,表明它们在优化过程中起到了关键作用。冷却性能与厚度的关系:随着每层薄膜厚度的逐步优化,冷却性能逐渐趋于稳定,优化算法成功调整了每层材料的厚度,以实现冷却效果与材料成本之间的平衡。通过该图,我们可以直观地看到优化过程中各层薄