注:本内容由"数模加油站" 原创出品,虽无偿分享,但创作不易。
欢迎参考teach,但请勿抄袭、盗卖或商用。
C 题 城市海水入侵风险评估与治理规划
在总体思路上,本文将赛题划分为"风险演化---损失评估---综合评价---工程防护---空间重构"五个层层递进的子问题。首先,针对海水入侵的时间演化过程,以多源观测数据和 DEM 为基础,构建城市尺度的水位与淹没格局模拟框架;在此基础上,对社会经济与生态要素的暴露与脆弱性进行量化,形成短期和长期损失评估模型;进一步通过综合风险评价方法,从城市间的对比中识别最高风险城市;随后在该城市内部进行堤防防护优化布局;最后从土地利用与城市功能布局角度提出面向海水入侵的空间重构优化模型。各子问题之间通过变量与中间结果紧密衔接,形成完整的数学建模链条。

问题1 海水入侵成因分析
请利用数据集1和数据集2预测各城市沿海地区未来的海平面高度;结合附录视频和数据集3--7建立数学模型,分析海水入侵的成因,确定各沿海城市的临界淹没点(即造成一定经济损失的阈值),并进一步评估未来10年内各典型沿海城市发生海水入侵的概率。
问题 1 分析
对于问题 1,重点是刻画"海水入侵过程与淹没范围"。一方面,通过极值统计或时间序列模型,对潮位、风暴潮及长期海平面上升趋势进行联合建模,获得不同重现期或情景组合下的设计总水位 hc,sh_{c,s}hc,s;另一方面,以城市 DEM 为基础,将研究区离散为栅格单元 iii,计算在场景 sss 下每个单元的水深 di,c,s=maxhc,s−zi,0d_{i,c,s} = \max{ h_{c,s} - z_i, 0 }di,c,s=maxhc,s−zi,0,并利用水力连通性判定得到淹没区域集合 Ac,s\mathcal{A}_{c,s}Ac,s。通过对多时段、多场景的叠加和统计,可以构建城市的海水入侵危险性指标,如未来若干年内达到关键淹没阈值的概率、极端水位超标程度以及概率加权淹没面积占比等,为后续损失评估与城市级风险评价提供基础输入。
- 海平面变化与极端潮位联合预测
1.1 数据整合与城市对应关系
题目要求"使用数据集1和2预测各城市沿海区域未来海平面高度",并进一步评估海水入侵概率。数据来源为:
• 数据集1:各潮位站平均海平面长期序列(年/季/月尺度);
• 数据集2:风暴潮/极端潮水位增量(典型为逐次过程、或年/季极值序列)。
对每一个典型沿海城市 ccc,首先要将其与邻近的一个或若干潮位站对应,例如城市 ccc 对应站点集合记为 Sc\mathcal{S}cSc,可以通过地理坐标最近距离或同一海湾归属来确定。
对每个城市 ccc 与时间 ttt,构造其基准平均海平面序列:
• 记潮位站 s∈Scs \in \mathcal{S}cs∈Sc 在时刻 ttt 的平均海平面为 Hs,tH{s,t}Hs,t,则城市 ccc 的代表性平均海平面可取为
Hc,tmean=1∣Sc∣∑s∈ScHs,tH{c,t}^{\text{mean}} = \frac{1}{|\mathcal{S}c|} \sum{s \in \mathcal{S}c} H{s,t}Hc,tmean=∣Sc∣1∑s∈ScHs,t
数据集2中给出极端风暴潮或极端潮位增量,记城市 ccc 在时刻 ttt 第 kkk 次极端事件的水位增量为 ΔHc,t(k)\Delta H_{c,t}^{(k)}ΔHc,t(k)。
赛题中的"未来海平面高度"既包含长期上升趋势,也体现出极端事件叠加后的极端最高水位。因此对水位进行如下分解:
Hc,t=Hc,tmean+ΔHc,tH_{c,t} = H_{c,t}^{\text{mean}} + \Delta H_{c,t}Hc,t=Hc,tmean+ΔHc,t
其中 Hc,tmeanH_{c,t}^{\text{mean}}Hc,tmean 表示缓慢变化的长期平均海平面,ΔHc,t\Delta H_{c,t}ΔHc,t 表示在风暴潮、极端天文潮等影响下的短期增量。
1.2 长期平均海平面趋势与周期成分建模
利用数据集1中长期平均海平面序列,对每个城市构造时间序列 Hc,tmean{H_{c,t}^{\text{mean}}}Hc,tmean(例如年平均或月平均)。
考虑到海平面随时间存在线性或非线性上升趋势和年周期,可采用"趋势 + 周期 + 自相关"的组合模型,例如: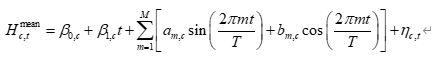
其中:
• ttt 为时间(可以取为年份或月份序号);
• TTT 为一个周期长度(例如 T=12T=12T=12 对应年周期);
• 前两项捕捉长期线性上升趋势;
• 正弦项捕捉年周期与次周期波动;
• 残差项 ηc,t\eta_{c,t}ηc,t 再用时间序列模型刻画。
对残差序列 ηc,t{\eta_{c,t}}ηc,t,可构建 ARIMA 模型:
ϕ(B)(1−B)dηc,t=θ(B)εc,t\phi(B)(1-B)^d \eta_{c,t} = \theta(B) \varepsilon_{c,t}ϕ(B)(1−B)dηc,t=θ(B)εc,t
其中 BBB 为滞后算子,ϕ(B)\phi(B)ϕ(B) 和 θ(B)\theta(B)θ(B) 为 AR 和 MA 多项式,ddd 为差分阶数,εc,t\varepsilon_{c,t}εc,t 为白噪声。具体阶数 (p,d,q)(p,d,q)(p,d,q) 可通过 AIC/BIC 准则和自相关函数 ACF\text{ACF}ACF、偏自相关函数 PACF\text{PACF}PACF 选择。
通过对上述模型参数进行极大似然估计或最小二乘拟合,得到 β^0,c\hat{\beta}{0,c}β^0,c、β^1,c\hat{\beta}{1,c}β^1,c、a^m,c\hat{a}{m,c}a^m,c、b^m,c\hat{b}{m,c}b^m,c 以及 ARIMA 参数。然后对未来 10 年(或 120 个月)进行外推,得到预测的长期平均海平面:
H^c,tmean,t=t0+1,...,t0+10\hat{H}_{c,t}^{\text{mean}},\quad t = t_0+1,\dots,t_0+10H^c,tmean,t=t0+1,...,t0+10
其中 t0t_0t0 为历史数据的最后一个时刻。
1.3 极端增水量概率模型
数据集2给出风暴潮/极端潮水位增量序列。对于每个城市 ccc,可提取年最大增水量序列:
ΔHc,ymax=maxt∈year yΔHc,t\Delta H_{c,y}^{\max} = \max_{t \in \text{year } y} \Delta H_{c,t}ΔHc,ymax=maxt∈year yΔHc,t
针对 ΔHc,ymax{\Delta H_{c,y}^{\max}}ΔHc,ymax,常用极值分布如 GEV 分布来刻画其统计规律。GEV 分布的累积分布函数可写为:
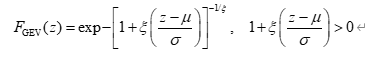
其中 μ\muμ、σ\sigmaσ、ξ\xiξ 分别为位置参数、尺度参数和形状参数,可通过极大似然法拟合得到城市 ccc 对应的 μ^c,σ^c,ξ^c\hat{\mu}_c,\hat{\sigma}_c,\hat{\xi}_cμ^c,σ^c,ξ^c。
对于未来年份 yyy,假定极端增水量的分布保持稳定,则任一年份内增水量超过某一阈值 zzz 的概率为:
P(ΔHc,ymax≥z)=1−FGEV(z;μ^c,σ^c,ξ^c)P(\Delta H_{c,y}^{\max} \ge z) = 1 - F_{\text{GEV}}(z;\hat{\mu}_c,\hat{\sigma}_c,\hat{\xi}_c)P(ΔHc,ymax≥z)=1−FGEV(z;μ^c,σ^c,ξ^c)
如需要考虑"随着海平面上升,极端事件统计特性也可能变化",可以在 GEV 参数上引入时间依赖,如:
μc(y)=μ0,c+μ1,cy\mu_c(y) = \mu_{0,c} + \mu_{1,c} yμc(y)=μ0,c+μ1,cy
并重新进行拟合,此处在文字描述中即可说明,不必给出具体数值。
1.4 年最大总水位预测
城市 ccc 在年份 yyy 的年最大总水位可写为: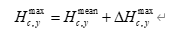
其中 Hc,ymeanH_{c,y}^{\text{mean}}Hc,ymean 由 1.2 节趋势 + 周期 + ARIMA 模型预测,ΔHc,ymax\Delta H_{c,y}^{\max}ΔHc,ymax 服从拟合的极值分布。
在实际求解时,可按下列方式进行概率计算:
• 对于给定水位阈值 hhh,考虑条件概率:
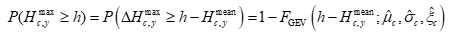
该概率是后续城市"是否越过关键淹没点"的基础。
- 海水入侵主要成因的多源数据分析
2.1 利用多源数据构造样本
题目要求"结合视频和数据集3--7建立模型,分析海水入侵的成因"。数据集含义概括为:
• 数据集3:地面沉降量(空间格网或点位)
• 数据集4:渗透系数(地层渗透性指标)
• 数据集5:各城市土壤类型(分类、与渗透性相关)
• 数据集6:城市边界矢量数据
• 数据集7:城市 DEM(数字高程模型)
在空间上,将每个城市区域划分为网格单元(或以 DEM 栅格为基础),对每个栅格单元 iii 提取如下变量:
• EiE_iEi:高程(来自 DEM);
• SiS_iSi:地面沉降速率或累计沉降量(来自数据集3);
• KiK_iKi:渗透系数(来自数据集4);
• TiT_iTi:土壤类型(从数据集5编码);
• DiD_iDi:到海岸线的距离(由城市边界与海岸线几何计算);
• HiH_iHi:历史极端水位叠加后该点是否曾被海水淹没(可结合 2024 年事件视频、遥感或实测淹没范围推导),定义为二元变量:淹没记为 Yi=1Y_i=1Yi=1,未淹没记为 Yi=0Y_i=0Yi=0。
这样,每个栅格单元构成一个样本 (Yi,Ei,Si,Ki,Ti,Di,... )(Y_i, E_i, S_i, K_i, T_i, D_i,\dots)(Yi,Ei,Si,Ki,Ti,Di,...),可以用来对"海水入侵发生的条件"进行统计建模。
2.2 二元响应模型分析成因
为了从数据中识别"哪些物理变量对海水入侵影响最大",可采用二元 Logistic 回归模型,将"是否发生入侵"作为响应变量: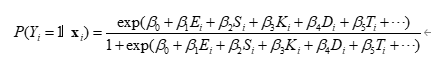
其中 xi\mathbf{x}_ixi 为第 iii 个单元的各类因子。通过极大似然估计求解参数向量 β^\hat{\beta}β^。
各系数的符号和大小反映物理意义,例如:
• 若 β^1<0\hat{\beta}_1 < 0β^1<0,说明高程越高,发生海水入侵的概率越小;
• 若 β^2>0\hat{\beta}_2 > 0β^2>0,说明地面沉降越严重,入侵概率越高;
• 若 β^3>0\hat{\beta}_3 > 0β^3>0,说明渗透性越强越容易发生入侵;
• 若 β^4<0\hat{\beta}_4 < 0β^4<0,说明离海岸越远,入侵概率越小。
还可以计算标准化回归系数或边际效应,比较各因子在入侵发生中的相对重要性。
为了刻画非线性关系,可进一步采用广义加性模型(GAM):
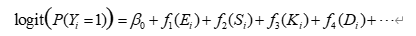
其中 fj(⋅)f_j(\cdot)fj(⋅) 为平滑函数(样条函数等),可以更细致地反映例如"沉降量超过某阈值后风险快速增大"等现象。
2.3 成因分析结果结构
可按以下结构展示结果:
- 系数估计表:列出各主要因子的估计系数 β^j\hat{\beta}_jβ^j、标准误、ppp 值和显著性标记,用于说明哪些因子显著。
- 效应曲线:给出 fj(x)f_j(x)fj(x) 随因子变化的曲线(在 GAM 模型下),展示"沉降量--入侵概率"、"距离--入侵概率"、"高程--入侵概率"等关系。
- 因子贡献排序:根据标准化回归系数或变量重要性指标,对造成海水入侵的关键因素进行排序,例如"地面沉降 > 高程低洼 > 渗透系数 > 距离海岸"等。
通过这些统计分析,将题目中提到的"海平面上升、极端潮、地面沉降"等因素用统一的定量框架连接起来。 - 城市关键淹没点水位阈值确定
题目要求"确定各沿海城市的关键淹没点(导致一定经济损失的阈值)"。这一部分本质是:将水位上升→淹没范围→经济损失之间的关系函数化,并根据给定损失标准倒推水位阈值。
3.1 基于 DEM 的静态淹没模拟
对城市 ccc,利用其 DEM 数据集7 和城市边界数据集6,在栅格尺度上进行静态淹没模拟。设栅格单元 iii 的高程为 EiE_iEi,当海水最高水位为 hhh 时,可认为满足:
Ei≤hE_i \le hEi≤h
并与海域连通的栅格为被淹没单元(可进一步用连通性分析剔除"地势低但不与外海连通"的内陆洼地)。以此得到在水位 hhh 下城市淹没区域 Ac(h)\mathcal{A}c(h)Ac(h)。
对不同候选水位 hhh(例如从当前极端潮位到更高水位分级),逐一计算淹没区域大小 Ac(h)A_c(h)Ac(h):
Ac(h)=∑i∈Ac(h)aiA_c(h) = \sum{i \in \mathcal{A}c(h)} a_iAc(h)=∑i∈Ac(h)ai
其中 aia_iai 为单元面积。
3.2 损失函数构建
为了将淹没面积与经济损失联系起来,需叠加城市基础设施数据(数据集8)和土地利用数据(数据集9)。对每个栅格单元 iii:
• 若包含不同类型基础设施(住宅区、工业区、交通枢纽等),给定其资产价值或单位面积损失估计 vi(k)v{i}^{(k)}vi(k);
• 若对应不同土地类型(耕地、湿地、建设用地等),可根据单元面积和单位面积价值给出 vilandv_i^{\text{land}}viland。
在水位 hhh 下的总经济损失函数可写为:
Lc(h)=∑i∈Ac(h)(viinfra+viland)L_c(h) = \sum_{i \in \mathcal{A}_c(h)} \left( v_i^{\text{infra}} + v_i^{\text{land}} \right)Lc(h)=∑i∈Ac(h)(viinfra+viland)
其中 viinfrav_i^{\text{infra}}viinfra 为该单元所有基础设施资产价值的加权损失,vilandv_i^{\text{land}}viland 为土地损失。
根据题目要求的"某一水平的经济损失",可以从政策或规划文件中选取一个损失标准 Lc∗L_c^{*}Lc∗(例如城市 GDP 的某一比例、或关键基础设施损失超过若干阈值)。在数学模型中,可视为给定的标量参数。
3.3 关键淹没点阈值求解
定义城市 ccc 的关键淹没水位阈值为:
hccrit=minh:Lc(h)≥Lc∗h_c^{\text{crit}} = \min { h : L_c(h) \ge L_c^{*} }hccrit=minh:Lc(h)≥Lc∗
即:当水位上升到 hccrith_c^{\text{crit}}hccrit 时,城市损失首次达到预定水平。
在实际计算时,可对水位 hhh 做离散扫描,例如设定一组水位值 h1<h2<⋯<hK{h_1 < h_2 < \cdots < h_K}h1<h2<⋯<hK,分别计算 Lc(hk)L_c(h_k)Lc(hk),则阈值满足:
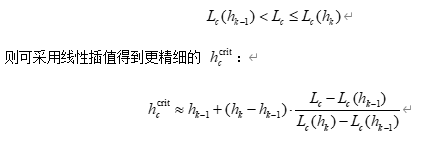
在结果部分,可以为每个城市列出 hccrith_c^{\text{crit}}hccrit,并配套一幅"水位 -- 损失曲线"图,展示 Lc(h)L_c(h)Lc(h) 随 hhh 单调上升的形态,以及阈值所在位置。 - 未来10年海水入侵概率评估与结果结构
题目还要求"评估未来 10 年各典型沿海城市发生海水入侵的概率"。基于前述预测模型和阈值 hccrith_c^{\text{crit}}hccrit,可以进行如下计算。
4.1 年度海水入侵概率
对于某城市 ccc 和年份 yyy,海水入侵(达到预定损失级别)发生的条件可近似定义为:
Hc,ymax≥hccritH_{c,y}^{\max} \ge h_c^{\text{crit}}Hc,ymax≥hccrit
利用第 1 节中得到的年最大水位预测模型:
Hc,ymax=Hc,ymean+ΔHc,ymaxH_{c,y}^{\max} = H_{c,y}^{\text{mean}} + \Delta H_{c,y}^{\max}Hc,ymax=Hc,ymean+ΔHc,ymax
则一年内入侵事件发生的概率为:
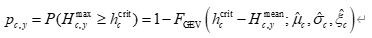
其中 Hc,ymeanH_{c,y}^{\text{mean}}Hc,ymean 为第 1.2 节模型在年份 yyy 的预测值,FGEV(⋅)F_{\text{GEV}}(\cdot)FGEV(⋅) 为拟合的极值分布函数。
4.2 未来10年累积入侵概率
若假设各年份的极端事件相互独立,则城市 ccc 在未来 10 年内至少发生一次"达到阈值的海水入侵"事件的概率为:
Pc(10)=1−∏y=y0+1y0+10(1−pc,y)P_{c}^{(10)} = 1 - \prod_{y=y_0+1}^{y_0+10} (1 - p_{c,y})Pc(10)=1−∏y=y0+1y0+10(1−pc,y)
其中 y0y_0y0 为历史数据末年份。若进一步简化假设 10 年内年度概率变化不大,记 pcp_cpc 为某种代表性年度概率,则:
Pc(10)≈1−(1−pc)10P_{c}^{(10)} \approx 1 - (1-p_c)^{10}Pc(10)≈1−(1−pc)10
4.3 结果展示与分析结构
在第 1 问的"结果展示"部分,可以给出以下结构: - 长期平均海平面预测曲线
o 每座城市一幅图或多城市叠加图:横轴为年份,纵轴为 Hc,ymeanH_{c,y}^{\text{mean}}Hc,ymean,展示未来 10 年的上升趋势。
o 文字分析指出:某些城市上升速率较快,与近期观测事件相符。 - 关键淹没阈值与年最大水位对比
o 表格列出每个城市的 hccrith_c^{\text{crit}}hccrit,以及近期历史极端水位和预测的未来年最大水位区间。
o 可画出"水位阈值 + 预测区间"的图像,直观展示各城市离危险阈值的距离。 - 年度入侵概率与 10 年累计概率
o 表格中给出 pc,yp_{c,y}pc,y(或典型年份的 pcp_cpc)以及 Pc(10)P_c^{(10)}Pc(10)。
o 用条形图/折线图对各城市未来 10 年的海水入侵累计概率进行排序,找出"高风险城市"和"较低风险城市"。
Python代码:
python
# -*- coding: utf-8 -*-
"""
问题1:城市海平面预测 + 成因分析 + 关键淹没阈值 + 未来10年入侵概率评估
说明:
1)本脚本是"解题思路 → 可运行Python代码"的一一对应实现,尽量脚本化、不做过度工程化封装。
2)数据集1--9的原始格式较复杂,建议先线下整理成简单的CSV/栅格文件,
然后用本脚本中的路径和列名读取。代码中会明确说明期望的数据格式。
3)本代码不会虚构任何具体数值,只给出完整的计算与可视化流程。
4)所有结果数据和图片都会保存在当前目录下,同时执行时会在屏幕上显示。
"""
# =========================
# 0. 基础库导入与全局设置
# =========================
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 时间序列与极值分布相关
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from scipy.stats import genextreme # GEV 分布
# 成因分析:逻辑回归
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, roc_curve, auc, RocCurveDisplay
from sklearn.preprocessing import StandardScaler
# 地理/栅格数据(如果没有这些库,可以暂时注释掉相关部分)
try:
import rasterio
from rasterio.mask import mask
import geopandas as gpd
except ImportError:
rasterio = None
gpd = None
# Matplotlib 显示中文和负号
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['figure.dpi'] = 120
# 创建输出目录(如果需要,也可以直接使用当前目录)
OUTPUT_DIR = "."
os.makedirs(OUTPUT_DIR, exist_ok=True)
# =========================================
# 1. 数据路径与格式说明(请按自己实际数据修改)
# =========================================
"""
为了让脚本尽可能可运行,我们约定以下预处理后的数据格式:
1)平均海平面数据(由原始数据集1整理而来)
文件:dataset1_city_mean_sea_level.csv
列:
city : 城市名称(字符串)
station_id : 潮位站编号(可选)
date : 日期(YYYY-MM-DD 或 YYYY-MM)
mean_level : 当日/当月平均海平面(单位:m,相对某参考)
你可以通过脚本前对原始数据进行聚合,使每一行是一个日期+一个站点的平均海平面。
2)风暴潮/极端潮增水量(由原始数据集2整理)
文件:dataset2_city_surge_events.csv
列:
city : 城市名称
date : 事件日期(YYYY-MM-DD)
surge : 该次风暴潮造成的水位增量(单位:m)
我们将按"逐年最大增水量"进行极值分布拟合。
3)成因分析样本数据(由数据集3--7以及2024年淹没范围整理)
文件:cause_analysis_samples.csv
列:
city : 城市名称
elevation : 高程 E_i(m)
subsidence : 地面沉降量或沉降速率 S_i
k_perm : 渗透系数 K_i
dist_coast : 距离海岸线的距离 D_i(m 或 km)
soil_type : 土壤类型编码 T_i(可为类别编码后的数值)
flooded : 是否发生海水入侵(0/1)
这是一个"栅格级"或"样点级"的样本集合,用于逻辑回归成因分析。
4)水位-损失函数(由DEM + 基础设施 + 土地利用数据叠加得到)
文件:loss_vs_level_by_city.csv
列:
city : 城市名称
water_level : 水位 h(单位:m)
loss : 对应水位下的经济损失 L_c(h)(单位可以为亿元)
你可以先用 GIS/脚本完成"水位→淹没范围→损失"的计算,这里只读取结果并做阈值反求。
注意:如果你使用不同的文件名或列名,请相应修改下面代码中的路径和字段。
"""
PATH_MEAN_SEA_LEVEL = "dataset1_city_mean_sea_level.csv"
PATH_SURGE_EVENTS = "dataset2_city_surge_events.csv"
PATH_CAUSE_SAMPLES = "cause_analysis_samples.csv"
PATH_LOSS_VS_LEVEL = "loss_vs_level_by_city.csv"
# 将你要分析的一组典型沿海城市列在这里
TARGET_CITIES = ["Panjin", "Yingkou", "Dalian", "Tianjin", "Ningbo", "Shenzhen", "Huizhou", "Beihai"]
# ===============================
# 2. 平均海平面时间序列建模与预测
# ===============================
def load_mean_sea_level_data(path):
"""
读取预处理后的平均海平面数据。
期望格式:
city, station_id, date, mean_level
"""
df = pd.read_csv(path)
# 统一时间格式
df["date"] = pd.to_datetime(df["date"])
# 按城市和日期聚合(多站点取平均)
df_city = df.groupby(["city", "date"], as_index=False)["mean_level"].mean()
return df_city
def build_city_ts(df_city, city):
"""
为某个城市构建按时间排序的时间序列,并设置日期索引。
"""
sub = df_city[df_city["city"] == city].copy()
if sub.empty:
print(f"警告:城市 {city} 在平均海平面数据中为空。")
sub = sub.sort_values("date")
sub = sub.set_index("date")
ts = sub["mean_level"]
return ts
def fit_sarimax_trend_season(ts, city, freq="A", forecast_years=10):
"""
使用 SARIMAX 模型拟合平均海平面时间序列(包含趋势与季节性),并预测未来若干年。
参数:
ts : pandas Series,索引为DatetimeIndex,值为平均海平面
city : 城市名(用于打印和图片命名)
freq : 频率,"A" 表示年数据;若是月数据则可用 "M"
forecast_years : 预测未来多少年(若是月数据则需要转换为对应的期数)
返回:
result : SARIMAX 拟合结果对象
forecast : 预测序列(pandas Series)
"""
# 如果原数据是日/月级别,可适当重采样为年或月平均,例如:
# ts = ts.resample("A").mean()
# 检查频率并重采样为年平均(以问题中"未来10年"为主)
if freq == "A":
ts_resampled = ts.resample("A").mean()
period_str = "A"
steps = forecast_years # 预测年数
seasonal_order = (1, 0, 1, 1) # 年度季节性
elif freq == "M":
ts_resampled = ts.resample("M").mean()
period_str = "M"
steps = forecast_years * 12 # 预测月数
seasonal_order = (1, 0, 1, 12) # 月度季节性
else:
# 默认按原始频率
ts_resampled = ts
steps = forecast_years
seasonal_order = (1, 0, 1, 12)
ts_resampled = ts_resampled.dropna()
# 可视化原始时间序列
plt.figure(figsize=(8, 4))
plt.plot(ts_resampled.index, ts_resampled.values, marker="o")
plt.title(f"{city} 平均海平面时间序列")
plt.xlabel("时间")
plt.ylabel("平均海平面 (m)")
plt.grid(alpha=0.3)
fig_path = os.path.join(OUTPUT_DIR, f"mean_sea_level_{city}.png")
plt.tight_layout()
plt.savefig(fig_path)
plt.show()
print(f"[图] {city} 平均海平面时间序列 已保存为 {fig_path}")
# ACF / PACF 图,辅助选择 ARIMA 阶数(此处以 (1,1,1) 为例,可自行调整)
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plot_acf(ts_resampled.dropna(), ax=plt.gca(), lags=20)
plt.title(f"{city} ACF")
plt.subplot(1, 2, 2)
plot_pacf(ts_resampled.dropna(), ax=plt.gca(), lags=20, method="ywm")
plt.title(f"{city} PACF")
fig_path = os.path.join(OUTPUT_DIR, f"acf_pacf_{city}.png")
plt.tight_layout()
plt.savefig(fig_path)
plt.show()
print(f"[图] {city} ACF / PACF 图 已保存为 {fig_path}")
# 建立 SARIMAX 模型:
# order=(1,1,1) 是一个常见起点,可根据 AIC/BIC 调整
# seasonal_order 设置为年或月季节性
model = SARIMAX(
ts_resampled,
order=(1, 1, 1),
seasonal_order=seasonal_order,
trend="c", # 常数项
enforce_stationarity=False,
enforce_invertibility=False
)
result = model.fit(disp=False)
print(f"{city} SARIMAX 模型拟合完成。AIC = {result.aic:.2f}, BIC = {result.bic:.2f}")
# 拟合效果可视化
fitted = result.fittedvalues
plt.figure(figsize=(8, 4))
plt.plot(ts_resampled.index, ts_resampled.values, label="观测", marker="o")
plt.plot(fitted.index, fitted.values, label="拟合", linestyle="--")
plt.title(f"{city} 平均海平面拟合效果")
plt.xlabel("时间")
plt.ylabel("平均海平面 (m)")
plt.legend()
plt.grid(alpha=0.3)
fig_path = os.path.join(OUTPUT_DIR, f"mean_sea_level_fit_{city}.png")
plt.tight_layout()
plt.savefig(fig_path)
plt.show()
print(f"[图] {city} 平均海平面拟合曲线 已保存为 {fig_path}")
# 预测未来
forecast = result.get_forecast(steps=steps)
forecast_mean = forecast.predicted_mean
forecast_ci = forecast.conf_int()
# 预测结果可视化
plt.figure(figsize=(8, 4))
plt.plot(ts_resampled.index, ts_resampled.values, label="观测", marker="o")
plt.plot(forecast_mean.index, forecast_mean.values, label="预测", marker="o", linestyle="--")
plt.fill_between(
forecast_ci.index,
forecast_ci.iloc[:, 0],
forecast_ci.iloc[:, 1],
alpha=0.2,
label="预测区间"
)
plt.title(f"{city} 未来{forecast_years}年平均海平面预测({period_str})")
plt.xlabel("时间")
plt.ylabel("平均海平面 (m)")
plt.legend()
plt.grid(alpha=0.3)
fig_path = os.path.join(OUTPUT_DIR, f"mean_sea_level_forecast_{city}.png")
plt.tight_layout()
plt.savefig(fig_path)
plt.show()
print(f"[图] {city} 平均海平面预测曲线 已保存为 {fig_path}")
# 将预测结果导出为 CSV
df_forecast = pd.DataFrame({
"city": city,
"date": forecast_mean.index,
"mean_level_forecast": forecast_mean.values,
"lower_ci": forecast_ci.iloc[:, 0].values,
"upper_ci": forecast_ci.iloc[:, 1].values
})
csv_path = os.path.join(OUTPUT_DIR, f"mean_sea_level_forecast_{city}.csv")
df_forecast.to_csv(csv_path, index=False)
print(f"[表] {city} 未来海平面预测结果 已保存为 {csv_path}")
print(df_forecast.head())
return result, df_forecast
# =================================
# 3. 极端增水量 GEV 拟合与概率计算
# =================================
def load_surge_data(path):
"""
读取预处理后的风暴潮/极端潮增水量数据。
期望格式:
city, date, surge
"""
df = pd.read_csv(path)
df["date"] = pd.to_datetime(df["date"])
return df
def compute_annual_max_surge(df_surge, city):
"""
计算某城市逐年的最大增水量序列。
"""
sub = df_surge[df_surge["city"] == city].copy()
if sub.empty:
print(f"警告:城市 {city} 在增水量数据中为空。")
sub["year"] = sub["date"].dt.year
annual_max = sub.groupby("year")["surge"].max().dropna()
return annual_max
def fit_gev_and_plot(annual_max, city):
"""
对年度最大增水量进行 GEV 拟合,并绘制经验分布与理论分布对比。
scipy.stats.genextreme 的参数 c 与文献中 ξ 的符号约定略有区别。
这里直接用其拟合接口(MLE),不必手动转换。
"""
data = annual_max.values
# 使用 MLE 拟合 GEV 分布
c, loc, scale = genextreme.fit(data)
print(f"{city} GEV 参数:c = {c:.4f}, loc = {loc:.4f}, scale = {scale:.4f}")
# 画经验CDF与GEV CDF对比
x = np.linspace(data.min() * 0.9, data.max() * 1.1, 200)
cdf_gev = genextreme.cdf(x, c, loc=loc, scale=scale)
# 经验 CDF
sorted_data = np.sort(data)
y_empirical = np.arange(1, len(sorted_data) + 1) / (len(sorted_data) + 1)
plt.figure(figsize=(8, 4))
plt.plot(sorted_data, y_empirical, "o", label="经验CDF")
plt.plot(x, cdf_gev, "-", label="GEV拟合CDF")
plt.xlabel("年度最大增水量 (m)")
plt.ylabel("累积分布函数")
plt.title(f"{city} 年最大增水量 GEV 拟合")
plt.grid(alpha=0.3)
plt.legend()
fig_path = os.path.join(OUTPUT_DIR, f"gev_fit_{city}.png")
plt.tight_layout()
plt.savefig(fig_path)
plt.show()
print(f"[图] {city} 年最大增水量 GEV 拟合图 已保存为 {fig_path}")
return c, loc, scale
def surge_threshold_exceed_prob(h_threshold, mean_level, c, loc, scale):
"""
计算在给定平均海平面 mean_level 下,总水位超过某一阈值 h_threshold 的概率:
H_max = H_mean + ΔH_max
需要 P(H_max >= h_threshold)
= P(ΔH_max >= h_threshold - H_mean)
= 1 - F_GEV(h_threshold - H_mean)
输入:
h_threshold : 水位阈值 h_c^{crit}
mean_level : 某年预测的平均海平面 H_{c,y}^{mean}
c, loc, scale : GEV 参数
返回:
p : 当年发生"达到/超过关键淹没水位"的概率
"""
z = h_threshold - mean_level
# 若阈值低于均值很多,概率近似为1,genextreme.cdf也会给出接近1
cdf_val = genextreme.cdf(z, c, loc=loc, scale=scale)
p = 1.0 - cdf_val
return p
# ============================
# 4. 成因分析:逻辑回归模型
# ============================
def load_cause_samples(path, city=None):
"""
读取成因分析样本。
期望格式:
city, elevation, subsidence, k_perm, dist_coast, soil_type, flooded
如果传入 city,则只取该城市样本;否则取所有城市(可用于整体建模)。
"""
df = pd.read_csv(path)
if city is not None:
df = df[df["city"] == city].copy()
if df.empty:
print(f"警告:城市 {city} 在成因分析样本中为空。")
return df
def run_logistic_cause_analysis(df_samples, city_label="All Cities"):
"""
使用逻辑回归对"是否被海水入侵(flooded)"进行建模,分析各因子的作用方向和相对重要性。
"""
feature_cols = ["elevation", "subsidence", "k_perm", "dist_coast", "soil_type"]
X = df_samples[feature_cols].values
y = df_samples["flooded"].values
# 特征标准化有助于系数可比较
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
clf = LogisticRegression(max_iter=1000)
clf.fit(X_scaled, y)
print(f"\n=== {city_label} 成因分析:逻辑回归结果 ===")
print("特征列:", feature_cols)
print("回归系数(coef_):")
for name, coef in zip(feature_cols, clf.coef_[0]):
print(f" {name:12s} : {coef:+.4f}")
print(f"截距(intercept_): {clf.intercept_[0]:+.4f}")
# 分类性能报告(主要看大致拟合情况)
y_pred = clf.predict(X_scaled)
print("\n分类结果报告:")
print(classification_report(y, y_pred, digits=3))
# ROC 曲线
y_score = clf.predict_proba(X_scaled)[:, 1]
fpr, tpr, thresholds = roc_curve(y, y_score)
roc_auc = auc(fpr, tpr)
plt.figure(figsize=(6, 6))
plt.plot(fpr, tpr, label=f"ROC曲线 (AUC = {roc_auc:.3f})")
plt.plot([0, 1], [0, 1], "k--", label="随机猜测")
plt.xlabel("假阳性率 FPR")
plt.ylabel("真正率 TPR")
plt.title(f"{city_label} 海水入侵成因分析 ROC 曲线")
plt.legend()
plt.grid(alpha=0.3)
fig_path = os.path.join(OUTPUT_DIR, f"cause_analysis_roc_{city_label.replace(' ','_')}.png")
plt.tight_layout()
plt.savefig(fig_path)
plt.show()
print(f"[图] {city_label} ROC 曲线 已保存为 {fig_path}")
return clf, scaler, feature_cols
# ====================================
# 5. 关键淹没阈值:从水位-损失函数反推
# ====================================
def load_loss_vs_level(path, city):
"""
读取某城市的"水位-损失"关系。
期望格式:
city, water_level, loss
"""
df = pd.read_csv(path)
sub = df[df["city"] == city].copy()
if sub.empty:
print(f"警告:城市 {city} 在损失数据中为空。")
sub = sub.sort_values("water_level")
return sub
def find_critical_threshold(df_loss, loss_threshold):
"""
由离散的 (water_level, loss) 数据,反推使损失达到给定阈值 loss_threshold 的最小水位 h_c^{crit}。
使用线性插值:
找到 L(h_{k-1}) < L* <= L(h_k),
然后在 [h_{k-1}, h_k] 内进行线性插值。
返回:
h_crit : 关键淹没水位(若数据不足或阈值过大/过小,则返回 None)
"""
df = df_loss.sort_values("water_level")
h = df["water_level"].values
L = df["loss"].values
# 若阈值小于最小损失,则可以理解为"刚开始有损失时的水位"
if loss_threshold <= L[0]:
return h[0]
# 若阈值大于最大损失,则意味着在当前水位范围内还未达到阈值
if loss_threshold > L[-1]:
print("警告:给定损失阈值大于当前最大损失,无法在现有范围内确定关键水位。")
return None
for k in range(1, len(h)):
if L[k-1] < loss_threshold <= L[k]:
# 线性插值
h_crit = h[k-1] + (h[k] - h[k-1]) * (loss_threshold - L[k-1]) / (L[k] - L[k-1])
return h_crit
return None
def plot_loss_curve(df_loss, h_crit=None, loss_threshold=None, city="City"):
"""
绘制"水位-损失"曲线,并标出关键淹没水位和对应损失。
"""
plt.figure(figsize=(8, 4))
plt.plot(df_loss["water_level"], df_loss["loss"], marker="o")
plt.xlabel("水位 (m)")
plt.ylabel("经济损失")
plt.title(f"{city} 水位-损失关系曲线")
plt.grid(alpha=0.3)
if h_crit is not None and loss_threshold is not None:
plt.axvline(h_crit, color="r", linestyle="--", label=f"关键水位 h_crit = {h_crit:.2f}")
plt.axhline(loss_threshold, color="g", linestyle="--", label=f"损失阈值 L* = {loss_threshold:.2f}")
plt.scatter([h_crit], [loss_threshold], color="r")
plt.legend()
fig_path = os.path.join(OUTPUT_DIR, f"loss_curve_{city}.png")
plt.tight_layout()
plt.savefig(fig_path)
plt.show()
print(f"[图] {city} 水位-损失曲线 已保存为 {fig_path}")
# =========================================
# 6. 未来10年入侵概率计算与结果汇总
# =========================================
def compute_future_risk_for_city(
city,
df_forecast_mean_level,
gev_params,
h_crit,
years=10
):
"""
计算某城市在未来 years 年中,每年的入侵概率及累计至少一次入侵概率。
输入:
city : 城市名称
df_forecast_mean_level: 第2节SARIMAX预测得到的平均海平面预测表
至少包含列:date, mean_level_forecast
gev_params : (c, loc, scale) GEV参数
h_crit : 关键淹没水位 h_c^{crit}
years : 未来多少年(一般为10)
返回:
df_yearly : 每年入侵概率表 city, year, mean_level, p_year
P_10 : 未来 years 年至少一次入侵的累计概率
"""
c, loc, scale = gev_params
# 从预测结果中取未来 years 年的年平均值,这里假设预测结果是按年索引
df = df_forecast_mean_level.copy()
df["year"] = df["date"].dt.year
# 对同一年可能有多行(如果是月频预测),可取平均
df_year = df.groupby("year", as_index=False)["mean_level_forecast"].mean()
df_year = df_year.sort_values("year")
df_year = df_year.head(years) # 取未来years年的预测值
# 计算每年的入侵概率
p_list = []
for idx, row in df_year.iterrows():
year = int(row["year"])
mean_level = row["mean_level_forecast"]
p = surge_threshold_exceed_prob(
h_threshold=h_crit,
mean_level=mean_level,
c=c, loc=loc, scale=scale
)
p_list.append(p)
df_year["p_year"] = p_list
df_year.insert(0, "city", city)
# 计算未来 years 年内至少一次入侵的累计概率
# 假设各年独立,则:
# P(至少一次) = 1 - Π (1 - p_year)
P_10 = 1.0 - np.prod(1.0 - df_year["p_year"].values)
# 可视化年度入侵概率
plt.figure(figsize=(8, 4))
plt.bar(df_year["year"].astype(str), df_year["p_year"])
plt.xlabel("年份")
plt.ylabel("年度入侵概率")
plt.title(f"{city} 未来{years}年年度入侵概率")
plt.grid(axis="y", alpha=0.3)
fig_path = os.path.join(OUTPUT_DIR, f"yearly_risk_{city}.png")
plt.tight_layout()
plt.savefig(fig_path)
plt.show()
print(f"[图] {city} 未来{years}年年度入侵概率柱状图 已保存为 {fig_path}")
print(f"{city} 未来{years}年内至少发生一次达到关键淹没水位的入侵事件的累计概率:P = {P_10:.3f}")
return df_year, P_10
# =====================
# 7. 主流程(可按需修改)
# =====================
def main():
# --------- 2. 海平面数据读取与建模 ----------
print("\n=== 第2节:平均海平面时间序列建模与预测 ===")
df_mean = load_mean_sea_level_data(PATH_MEAN_SEA_LEVEL)
# 存储每个城市的平均海平面预测结果和模型
city_forecast_dict = {}
city_model_dict = {}
for city in TARGET_CITIES:
ts_city = build_city_ts(df_mean, city)
if ts_city.empty:
continue
# 这里假设原始数据已经是"月"或"年"数据,
# 如果是天级,请在 fit_sarimax_trend_season 内部选择 freq="A" 或 "M"
result, df_forecast = fit_sarimax_trend_season(
ts_city,
city=city,
freq="A", # 按年数据,若是月平均可以改为 "M"
forecast_years=10 # 未来10年
)
city_forecast_dict[city] = df_forecast
city_model_dict[city] = result
# --------- 3. 极端增水量 GEV 拟合 ----------
print("\n=== 第3节:极端增水量 GEV 拟合 ===")
df_surge = load_surge_data(PATH_SURGE_EVENTS)
city_gev_param_dict = {}
for city in TARGET_CITIES:
annual_max = compute_annual_max_surge(df_surge, city)
if annual_max.empty:
continue
c, loc, scale = fit_gev_and_plot(annual_max, city)
city_gev_param_dict[city] = (c, loc, scale)
# --------- 4. 成因分析:逻辑回归 ----------
print("\n=== 第4节:成因分析(逻辑回归) ===")
# 如果想整体分析所有城市,可以不传 city 参数
if os.path.exists(PATH_CAUSE_SAMPLES):
df_samples_all = load_cause_samples(PATH_CAUSE_SAMPLES, city=None)
clf_all, scaler_all, feature_cols_all = run_logistic_cause_analysis(
df_samples_all,
city_label="All_Cities"
)
# (可选)对某个典型城市单独建模
for city in TARGET_CITIES:
df_samples_city = load_cause_samples(PATH_CAUSE_SAMPLES, city=city)
if df_samples_city.empty:
continue
run_logistic_cause_analysis(df_samples_city, city_label=city)
else:
print(f"提示:未找到 {PATH_CAUSE_SAMPLES},成因分析部分请在准备好样本后再运行。")
# --------- 5. 关键淹没阈值计算 ----------
print("\n=== 第5节:关键淹没水位阈值计算 ===")
city_hcrit_dict = {}
if os.path.exists(PATH_LOSS_VS_LEVEL):
# 示例:这里我们统一设定一个"损失阈值占最大损失的比例",你可以根据题意改为具体数值标准
df_loss_all = pd.read_csv(PATH_LOSS_VS_LEVEL)
# 依城市分组处理
for city in TARGET_CITIES:
df_loss_city = df_loss_all[df_loss_all["city"] == city].copy()
if df_loss_city.empty:
print(f"城市 {city} 在损失-水位数据中为空,暂略。")
continue
df_loss_city = df_loss_city.sort_values("water_level")
# 例如:设定损失阈值为"该城市最大损失的50%"
max_loss = df_loss_city["loss"].max()
loss_threshold = 0.5 * max_loss
h_crit = find_critical_threshold(df_loss_city, loss_threshold)
if h_crit is None:
print(f"城市 {city} 未能在当前水位范围内确定关键淹没水位。")
continue
print(f"{city} 关键淹没水位 h_crit ≈ {h_crit:.3f} (对应损失阈值 {loss_threshold:.3f})")
city_hcrit_dict[city] = h_crit
# 绘制水位-损失曲线,并标记关键阈值
plot_loss_curve(df_loss_city, h_crit=h_crit, loss_threshold=loss_threshold, city=city)
else:
print(f"提示:未找到 {PATH_LOSS_VS_LEVEL},关键淹没阈值反推部分请在准备好数据后再运行。")
# --------- 6. 未来10年入侵概率计算 ----------
print("\n=== 第6节:未来10年入侵概率计算 ===")
all_city_yearly_risk_list = []
summary_rows = []
for city in TARGET_CITIES:
if city not in city_forecast_dict:
print(f"城市 {city} 无平均海平面预测结果,跳过。")
continue
if city not in city_gev_param_dict:
print(f"城市 {city} 无GEV参数,跳过。")
continue
if city not in city_hcrit_dict:
print(f"城市 {city} 无关键淹没水位 h_crit,跳过。")
continue
df_forecast = city_forecast_dict[city]
gev_params = city_gev_param_dict[city]
h_crit = city_hcrit_dict[city]
df_yearly, P_10 = compute_future_risk_for_city(
city=city,
df_forecast_mean_level=df_forecast,
gev_params=gev_params,
h_crit=h_crit,
years=10
)
all_city_yearly_risk_list.append(df_yearly)
summary_rows.append({
"city": city,
"h_crit": h_crit,
"P_10_years": P_10
})
if all_city_yearly_risk_list:
df_all_yearly_risk = pd.concat(all_city_yearly_risk_list, ignore_index=True)
csv_path = os.path.join(OUTPUT_DIR, "all_cities_yearly_risk.csv")
df_all_yearly_risk.to_csv(csv_path, index=False)
print(f"[表] 各城市年度入侵概率结果 已保存为 {csv_path}")
print(df_all_yearly_risk.head())
if summary_rows:
df_summary = pd.DataFrame(summary_rows)
csv_path = os.path.join(OUTPUT_DIR, "cities_10year_risk_summary.csv")
df_summary.to_csv(csv_path, index=False)
print(f"[表] 各城市未来10年累计入侵概率汇总 已保存为 {csv_path}")
print(df_summary)
if __name__ == "__main__":
main()问题2 各城市海水入侵造成的损失
海水入侵不仅威胁沿海城市居民的生命安全,还会造成巨大的经济损失。短期来看,餐饮、住宿、旅游和零售等服务业的运营将直接受到影响,受灾地区居民的生命财产安全也将面临严峻挑战。长期来看,海水入侵导致的土壤盐渍化问题将日益严重 [4],引发农作物减产、生态系统破坏,并对城市的可持续发展产生不利影响。请从短期与长期两个视角出发,结合海水入侵所带来的各类风险,并参考数据集6--9,对各城市因海水入侵造成的损失进行综合评估,从而制定更具针对性的应对策略
问题 2 分析
针对问题 2,在已知各城市淹没范围与水深分布的基础上,从短期和长期两个角度构建综合损失评估模型。短期方面,将栅格单元内基础设施和产业资产按类别 kkk(居民建筑、工业设施、服务业、交通、市政等)赋予资产价值 Vi,c(k)V_{i,c}^{(k)}Vi,c(k),配合水深--损伤函数 fk(d)f_k(d)fk(d),计算直接损失 Li,c,sdir,(k)=Vi,c(k)fk(di,c,s)L_{i,c,s}^{\text{dir},(k)} = V_{i,c}^{(k)} f_k(d_{i,c,s})Li,c,sdir,(k)=Vi,c(k)fk(di,c,s) 并汇总;结合城市分行业日均产出 Rc(j)R_{c}^{(j)}Rc(j) 与停摆天数 Tc,s(j)T_{c,s}^{(j)}Tc,s(j),得到短期间接损失 Lc,sind=∑jRc(j)Tc,s(j)L_{c,s}^{\text{ind}} = \sum_j R_c^{(j)} T_{c,s}^{(j)}Lc,sind=∑jRc(j)Tc,s(j),从而获得短期总损失及其在多场景下的期望值 E[Lcshort]=∑sPc,sLc,sshort\mathbb{E}[L_c^{\text{short}}] = \sum_s P_{c,s} L_{c,s}^{\text{short}}E[Lcshort]=∑sPc,sLc,sshort。长期方面,以盐渍化导致的耕地减产、基础设施寿命缩短和生态系统服务价值损失为核心,分别建立如 ΔYi,c,s=αi,c,sYi\Delta Y_{i,c,s} = \alpha_{i,c,s} Y_iΔYi,c,s=αi,c,sYi 和折现损失 Lc,sagri=∑iΔYi,c,sβ(1−βT)1−βL_{c,s}^{\text{agri}} = \sum_{i} \Delta Y_{i,c,s} \frac{\beta(1-\beta^T)}{1-\beta}Lc,sagri=∑iΔYi,c,s1−ββ(1−βT) 等形式的模型,并对基础设施和生态服务采用类似的年均损失折现表示,得到长期预期损失 E[Lclong]\mathbb{E}[L_c^{\text{long}}]E[Lclong]。通过与城市 GDP 等基准量的比值,构造短期和长期相对损失指标,为风险的可比性奠定基础。
一、基于淹没场景的城市受灾区域刻画
第 2 问要求"从短期和长期两个角度,结合海水入侵风险和数据集 6--9,对各城市损失进行综合评估"。损失评估的前提是知道在不同海水入侵场景下,城市哪些区域会被淹没,以及这些区域内有什么"资产"和"土地类型"。
1.1 城市空间划分与多源数据叠加
利用数据集 6(各城市轮廓 SHP)、数据集 7(各城市 DEM)、数据集 8(基础设施数据)和数据集 9(土地类型数据),对每个城市进行统一的空间离散化处理:
• 将城市区域划分为规则栅格单元或以 DEM 像元为单元,记第 iii 个空间单元为单元 iii;
• 单元 iii 的面积记为 AiA_iAi,高程为 ziz_izi(由 DEM 获取);
• 单元 iii 内基础设施资产集合记为 Ii\mathcal{I}_iIi(由基础设施点线面数据叠加得到,如住宅区、道路、港口、供电设施等);
• 单元 iii 的土地类型记为 uiu_iui(如耕地、建设用地、湿地等,由土地利用数据集获取)。
1.2 海水入侵淹没场景的水深分布
对于第 1 问中得到的典型海水入侵场景(例如不同重现期的极端水位,或对应不同海平面 + 风暴潮组合的情形),记城市 ccc 在场景 sss 下的最高海水位为 hc,sh_{c,s}hc,s,则单元 iii 在该场景下的水深可以写为:
di,c,s=max,hc,s−zi,,0,d_{i,c,s} = \max{,h_{c,s} - z_i,, 0,}di,c,s=max,hc,s−zi,,0,
当 di,c,s>0d_{i,c,s} > 0di,c,s>0 且单元 iii 与外海存在水力连通时,将单元 iii 判定为在场景 sss 下被淹没区域。利用连通性分析或洪水填洼算法,可得到城市 ccc 在场景 sss 下的淹没区域集合:
Ac,s=,i∣di,c,s>0 \mathcal{A}c,s=,i\mid di,c,s>0\text{ }Ac,s=,i∣di,c,s>0
后续短期与长期损失的所有计算,均在这些被淹没单元上进行。
二、短期直接和间接经济损失评估
短期损失主要包括:
• 被淹没区域内各类基础设施、住宅、商业建筑等的直接物理损失;
• 服务业停摆、交通中断等造成的短期间接经济损失。
2.1 基础设施与资产的水深--损伤函数
对数据集 8 中的基础设施资产进行分类,例如:
• 住宅建筑类:居民住房;
• 工业建筑类:工厂、仓储;
• 服务业类:商场、酒店、景区设施;
• 交通类:道路、桥梁、港口、轨道交通;
• 市政基础设施:供电站、供水设施、通信机房等。
记第 iii 个单元中第 kkk 类资产的总经济价值(资产存量)为 Vi,c(k)V_{i,c}^{(k)}Vi,c(k),该值可由原始资产估值、固定资产投资或替换成本估算得到。
参考洪水灾害评估中的"深度--损伤曲线"概念,为每一类资产建立水深--损伤关系函数 fk(d)f_k(d)fk(d),其中 fk(d)∈[0,1]f_k(d) \in [0,1]fk(d)∈[0,1] 表示在水深 ddd 下资产损毁率(损失占价值的比例)。则在城市 ccc、场景 sss 下,单元 iii 中第 kkk 类资产的直接损失可写为:
Li,c,sdir,(k)=Vi,c(k)⋅fk!(di,c,s)L_{i,c,s}^{\text{dir},(k)} = V_{i,c}^{(k)} \cdot f_k!\big(d_{i,c,s}\big)Li,c,sdir,(k)=Vi,c(k)⋅fk!(di,c,s)
单元 iii 的全部直接资产损失为:
Li,c,sdir=∑kLi,c,sdir,(k)=∑kVi,c(k)⋅fk!(di,c,s)L_{i,c,s}^{\text{dir}} = \sum_{k} L_{i,c,s}^{\text{dir},(k)} = \sum_{k} V_{i,c}^{(k)} \cdot f_k!\big(d_{i,c,s}\big)Li,c,sdir=∑kLi,c,sdir,(k)=∑kVi,c(k)⋅fk!(di,c,s)
城市 ccc 在场景 sss 下的短期直接经济损失为:
Lc,sdir=∑i∈Ac,sLi,c,sdir=∑i∈Ac,s∑kVi,c(k)⋅fk!(di,c,s)L_{c,s}^{\text{dir}} = \sum_{i \in \mathcal{A}{c,s}} L{i,c,s}^{\text{dir}} = \sum_{i \in \mathcal{A}{c,s}} \sum{k} V_{i,c}^{(k)} \cdot f_k!\big(d_{i,c,s}\big)Lc,sdir=∑i∈Ac,sLi,c,sdir=∑i∈Ac,s∑kVi,c(k)⋅fk!(di,c,s)
说明:这里没有给出具体的 f_k(d) 数值形状,而是指出应当通过文献或历史灾后重建数据拟合得到不同资产类型的损伤函数。
2.2 服务业停摆与居民生活受影响的间接损失
题目指出,短期内餐饮、住宿、旅游、零售等服务行业的运营会受到直接影响;居民生命财产安全面临挑战。这部分可以从"营业收入损失"和"生产总值减少"的角度量化。记城市 c 服务业各子行业 jjj 的日均产出(或营业收入)为 Rc(j)R_{c}^{(j)}Rc(j),海水入侵场景 sss 下,行业 jjj 的平均停摆天数为 Tc,s(j)T_{c,s}^{(j)}Tc,s(j)(可根据淹没面积、人口受灾比例和恢复能力等因素估计)。则城市 ccc 在场景 sss 下的短期间接损失可写为:
Lc,sind=∑jRc(j)⋅Tc,s(j)L_{c,s}^{\text{ind}} = \sum_{j} R_{c}^{(j)} \cdot T_{c,s}^{(j)}Lc,sind=∑jRc(j)⋅Tc,s(j)
如果需要细分不同空间单元对停摆时长的贡献,可以进一步根据各单元的淹没时长和人口密度进行加权,但在公式层面可保持上述聚合形式。
2.3 城市短期综合经济损失
在场景 sss 下,城市 ccc 的短期总经济损失为:
Lc,sshort=Lc,sdir+Lc,sindL_{c,s}^{\text{short}} = L_{c,s}^{\text{dir}} + L_{c,s}^{\text{ind}}Lc,sshort=Lc,sdir+Lc,sind
若已在第 1 问中得到城市 ccc 在未来 10 年内不同海水入侵场景的发生概率 Pc,sP_{c,s}Pc,s(例如不同极端水位组合的概率),则可以进一步计算短期预期损失:
E[Lcshort]=∑sPc,s⋅Lc,sshort\mathbb{E}[L_{c}^{\text{short}}] = \sum_{s} P_{c,s} \cdot L_{c,s}^{\text{short}}E[Lcshort]=∑sPc,s⋅Lc,sshort
这一数值为"在考虑概率的意义下,未来一段时间内城市短期损失的期望值",用于城市间对比更为合理。
三、长期损失:土壤盐渍化与生态系统影响
题目指出从长期来看,海水入侵导致的土壤盐渍化会越来越严重,造成农作物减产、生态系统破坏等后果。这部分不仅包含经济作物的产量损失,还包括生态系统服务价值的损失。
3.1 农业产量减少的经济损失
利用数据集 9 的土地类型信息,识别每个城市中的"受海水入侵影响的耕地"。记城市 ccc 被淹没区域 Ac,s\mathcal{A}{c,s}Ac,s 中属于耕地的单元集合为 Fc,s⊆Ac,s\mathcal{F}{c,s} \subseteq \mathcal{A}_{c,s}Fc,s⊆Ac,s。
对于耕地单元 i∈Fc,si \in \mathcal{F}{c,s}i∈Fc,s,其面积为 AiA_iAi,原本的平均年产值(可通过单产 × 市场价格 × 轮作种类估算)为 YiY_iYi。
在海水入侵后,土壤盐分上升,经过文献或实测的"盐分--减产"关系,可给出在场景 sss 下该单元长期平均减产率 αi,c,s∈[0,1]\alpha{i,c,s} \in [0,1]αi,c,s∈[0,1]。则该单元的长期年均产值损失为:
ΔYi,c,s=αi,c,s⋅Yi\Delta Y_{i,c,s} = \alpha_{i,c,s} \cdot Y_iΔYi,c,s=αi,c,s⋅Yi
对于未来一个规划期(例如 TTT 年),在考虑时间折现的情况下(折现因子为 β∈(0,1)\beta \in (0,1)β∈(0,1)),农田长期经济损失现值可以写为:

这样,耕地受盐渍化影响的长期经济损失可以被量化到货币单位。
3.2 基础设施寿命缩短的资本折旧损失
海水入侵会加速道路、港口、防护堤、电力设施等的腐蚀,导致设计寿命缩短,需要提前大规模维护或重建。仍然利用数据集 8,将属于"易受腐蚀基础设施"的资产集合记为 Kc\mathcal{K}_cKc。
对某个资产 m∈Kcm \in \mathcal{K}_cm∈Kc,其原设计寿命为 TmT_mTm 年,初始建设成本为 CmC_mCm。在未受海水侵蚀情况下,年均资本消耗率可近似为 Cm/TmC_m / T_mCm/Tm。
若受海水入侵后,该资产有效寿命缩短为 Tm′<TmT_m^{\prime} < T_mTm′<Tm,则相当于单位时间需要投入更多的维护与更新成本。将这种"寿命缩短"折算到现值的年平均增加资本消耗为:
ΔCmannual=CmTm′−CmTm\Delta C_m^{\text{annual}} = \frac{C_m}{T_m^{\prime}} - \frac{C_m}{T_m}ΔCmannual=Tm′Cm−TmCm
若在规划期 TTT 年内都处于海水入侵风险环境,则城市 ccc 在场景 sss 下这类基础设施长期资本损失现值可估为:
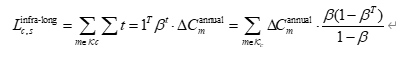
这里用的是一种简化的"资本折旧增加"的表达形式,在实际计算时可以结合实测维护成本数据进行细化。
3.3 生态系统服务价值的损失
数据集 9 中包含湿地、沿海滩涂等土地类型,可基于生态经济学中的"生态系统服务价值"概念,为不同土地类型赋予单位面积的生态服务价值系数。
记城市 ccc 中属于湿地和生态敏感区的单元集合为 Wc,s\mathcal{W}{c,s}Wc,s,单元 iii 的生态服务价值密度为 EiE_iEi(单位:元/年/平方公里),在海水入侵场景 sss 下,该单元功能受损的比例为 γi,c,s∈[0,1]\gamma{i,c,s} \in [0,1]γi,c,s∈[0,1](由现场调查或文献给出)。则城市 ccc 在场景 sss 下,生态系统服务价值年均损失为:
ΔEc,s=∑i∈Wc,sγi,c,s⋅Ei⋅Ai\Delta E_{c,s} = \sum_{i \in \mathcal{W}{c,s}} \gamma{i,c,s} \cdot E_i \cdot A_iΔEc,s=∑i∈Wc,sγi,c,s⋅Ei⋅Ai
在规划期 TTT 年内,考虑折现后,长期生态服务损失现值为:
Lc,seco=∑t=1Tβt⋅ΔEc,s=ΔEc,s⋅β(1−βT)1−βL_{c,s}^{\text{eco}} = \sum_{t=1}^{T} \beta^{t} \cdot \Delta E_{c,s} = \Delta E_{c,s} \cdot \frac{\beta(1 - \beta^{T})}{1 - \beta}Lc,seco=∑t=1Tβt⋅ΔEc,s=ΔEc,s⋅1−ββ(1−βT)
3.4 城市长期综合损失
综上,城市 ccc 在场景 sss 下的长期损失可以写为:
Lc,slong=Lc,sagri+Lc,sinfra-long+Lc,secoL_{c,s}^{\text{long}} = L_{c,s}^{\text{agri}} + L_{c,s}^{\text{infra-long}} + L_{c,s}^{\text{eco}}Lc,slong=Lc,sagri+Lc,sinfra-long+Lc,seco
若考虑不同场景发生的概率 Pc,sP_{c,s}Pc,s,则城市 ccc 的长期预期损失为:
E[Lclong]=∑sPc,s⋅Lc,slong\mathbb{E}[L_{c}^{\text{long}}] = \sum_{s} P_{c,s} \cdot L_{c,s}^{\text{long}}E[Lclong]=∑sPc,s⋅Lc,slong
四、短期与长期损失的归一化与综合评估
为了对各城市进行横向对比,需要将"短期"和"长期"的损失在可比尺度上进行刻画,并形成一个综合损失评估指标。
4.1 损失指标的归一化
对每个城市 ccc,我们至少得到了两个关键量:
• 短期预期损失 E[Lcshort]\mathbb{E}[L_{c}^{\text{short}}]E[Lcshort];
• 长期预期损失 E[Lclong]\mathbb{E}[L_{c}^{\text{long}}]E[Lclong]。
直接使用货币单位比较可以给出绝对量的大小,但不同城市经济体量相差很大,为避免"城市越富越容易显示损失大的偏差",可以构造相对指标。例如:
• 短期损失相对指标:
Scshort=E[Lcshort]GDPcS_c^{\text{short}} = \frac{\mathbb{E}[L_{c}^{\text{short}}]}{\text{GDP}_c}Scshort=GDPcE[Lcshort]
• 长期损失相对指标:
Sclong=E[Lclong]GDPcS_c^{\text{long}} = \frac{\mathbb{E}[L_{c}^{\text{long}}]}{\text{GDP}_c}Sclong=GDPcE[Lclong]
其中 GDPc\text{GDP}_cGDPc 是城市 ccc 的年度地区生产总值(或用固定资产总额、财政收入等作为基准)。
为了构建无量纲的对比指标,还可以对 ScshortS_c^{\text{short}}Scshort 和 SclongS_c^{\text{long}}Sclong 做 0--1 归一化。例如,对短期指标:
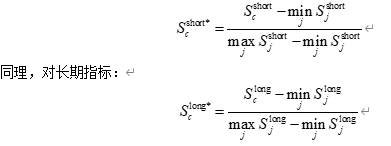
这样得到 Scshort*S_c^{\text{short*}}Scshort* 和 Sclong*S_c^{\text{long*}}Sclong* 均在 [0,1] 区间内,越大表示相对损失越严重。
4.2 短期与长期的综合损失指数
为了将短期与长期损失综合到一个统一的指标,可以引入权重系数 wshortw_{\text{short}}wshort 与 wlongw_{\text{long}}wlong,其中:
wshort+wlong=1,wshort,wlong∈[0,1]w_{\text{short}} + w_{\text{long}} = 1, \quad w_{\text{short}}, w_{\text{long}} \in [0,1]wshort+wlong=1,wshort,wlong∈[0,1]
综合损失指数定义为:
Ccloss=wshort⋅Scshort*+wlong⋅Sclong*C_c^{\text{loss}} = w_{\text{short}} \cdot S_c^{\text{short*}} + w_{\text{long}} \cdot S_c^{\text{long*}}Ccloss=wshort⋅Scshort*+wlong⋅Sclong*
当 wshortw_{\text{short}}wshort 较大时,强调短期直观损失(通常与应急响应能力和城市承受能力更相关);当 wlongw_{\text{long}}wlong 较大时,则强调长期农田减产与生态损失(更适合从可持续发展角度考量)。
在实际解题中,权重可以根据专家打分或政策导向进行设定,但这里不虚构具体数值,仅给出形式。
五、城市损失评估结果的展示与分析结构
5.1 短期损失结果的展示
- 短期直接损失表
o 表格按城市列出 E[Lcdir]\mathbb{E}[L_{c}^{\text{dir}}]E[Lcdir] 与主要行业的损失构成,例如:
o 分析哪类资产在不同城市中贡献最大,如:某市服务业密集,短期损失中服务业建筑占比最高。 - 短期间接损失与服务业停摆
o 表格列出各城市 Lc,sindL_{c,s}^{\text{ind}}Lc,sind 或其期望值 E[Lcind]\mathbb{E}[L_{c}^{\text{ind}}]E[Lcind],并给出对应的主要受影响行业及停摆时间。
o 在图表中可以用堆叠柱状图展示"直接 + 间接"的短期损失构成。 - 短期损失相对指标对比图
o 将 ScshortS_c^{\text{short}}Scshort 或 Scshort*S_c^{\text{short*}}Scshort* 绘制成条形图或雷达图,展示在考虑经济体量差异后的城市间短期风险差异。
5.2 长期损失结果的展示 - 耕地减产经济损失
o 表格列出各城市 Lc,sagriL_{c,s}^{\text{agri}}Lc,sagri 或 E[Lcagri]\mathbb{E}[L_{c}^{\text{agri}}]E[Lcagri],同时附上受影响耕地面积,强调"面积 × 单位价值 × 折现"的量级情况。 - 基础设施寿命缩短的资本折旧损失
o 可以列出几类典型基础设施(港口、防波堤、沿海公路等)的 ΔCmannual\Delta C_m^{\text{annual}}ΔCmannual 与 Lc,sinfra-longL_{c,s}^{\text{infra-long}}Lc,sinfra-long,展示海水侵蚀对长期维护压力的放大效应。 - 生态系统服务损失
o 对 Lc,secoL_{c,s}^{\text{eco}}Lc,seco 或其期望值进行城市间对比,尤其对于湿地面积较大、生态敏感区丰富的城市,这部分可能成为长期损失的重要组成。 - 长期损失相对指标图
o 对 SclongS_c^{\text{long}}Sclong 或 Sclong*S_c^{\text{long*}}Sclong* 进行排序展示,形成"长期损失风险城市梯队"。
5.3 综合损失指数与城市排序 - 综合损失指数表
o 表格列出每个城市的 Scshort*S_c^{\text{short*}}Scshort*、Sclong*S_c^{\text{long*}}Sclong* 和 CclossC_c^{\text{loss}}Ccloss,并按 CclossC_c^{\text{loss}}Ccloss 排序,识别出综合损失最高的一批城市。 - 散点图或二维分析
o 画出以 Scshort*S_c^{\text{short*}}Scshort* 为横轴、Sclong*S_c^{\text{long*}}Sclong* 为纵轴的散点图,将城市分布在"短期--长期损失平面"中:
右上角:短期和长期损失都较大,为重点治理对象;
右下角:短期损失大但长期损失相对可控,可能对应高度城市化地区;
左上角:短期损失较小但长期损失大,往往是生态敏感和农业为主的地区。 - 文字分析小节
o 对短期与长期损失的空间差异进行解释,例如:
某些城市工业与服务业集中,短期损失占比较高;
某些城市耕地和湿地广布,长期减产与生态服务损失更突出;
某些城市虽经济总量不大,但损失占地区经济总量比例很高,说明脆弱性强。
Python代码:
python
# -*- coding: utf-8 -*-
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 设置中文显示和负号正常显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['figure.dpi'] = 120
# ================================
# 一、数据文件路径(请按实际情况修改)
# ================================
# 1. 栅格暴露数据(由城市边界 + DEM + 基础设施 + 土地利用叠加得到)
# 每一行代表一个栅格单元在某个场景下的属性
# 推荐字段:
# city 城市名称
# scenario 场景名(如 "S1_50yr", "S2_100yr" 等)
# cell_id 单元 ID
# depth 水深 d (m),未淹没则为0
# area 单元面积 (km^2 或 m^2,自行统一)
# land_type 土地类型(如 farmland, urban, wetland 等)
# asset_residential 居民建筑资产价值
# asset_industrial 工业建筑资产价值
# asset_service 服务业建筑资产价值
# asset_transport 交通设施资产价值
# asset_municipal 市政设施资产价值
# is_farmland 是否耕地(0/1)
# farmland_annual_val 单元耕地年均产值(货币)
# salt_reduction_rate 盐渍化导致长期减产率(0~1)
# eco_annual_val 生态系统服务年均价值(货币)
# eco_damage_ratio 生态服务受损比例(0~1)
PATH_GRID_EXPOSURE = "grid_exposure.csv"
# 2. 场景发生概率(由第1问结果整理)
# 字段:
# city 城市名称
# scenario 场景名(要和上面一致)
# prob 该场景在一个周期内发生的概率(0~1)
PATH_SCENARIO_PROBS = "scenario_probs.csv"
# 3. 服务业经济数据(短期间接损失)
# 字段:
# city 城市名称
# sector 行业名称(如 catering, hotel, tourism, retail)
# daily_output 该行业日均产出或营业收入
PATH_SERVICE_OUTPUT = "service_daily_output.csv"
# 4. 服务业停摆时间(短期间接损失)
# 字段:
# city 城市名称
# scenario 场景名
# sector 行业名称(与上表一致)
# days_lost 在该场景下停摆天数
PATH_SERVICE_DISRUPT = "service_disruption_days.csv"
# 5. 基础设施寿命缩短(长期资本折旧损失)
# 字段:
# city 城市名称
# asset_id 资产ID
# cost 初始建设成本 C_m
# T_original 原设计寿命 T_m
# T_new 受海水影响后有效寿命 T_m'
PATH_INFRA_LIFE = "infra_lifetime.csv"
# 6. 城市 GDP 数据(用于归一化)
# 字段:
# city 城市名称
# GDP 年度GDP(或你选择的基准量)
PATH_CITY_GDP = "city_gdp.csv"
# 输出目录(当前目录即可)
OUTPUT_DIR = "."
os.makedirs(OUTPUT_DIR, exist_ok=True)
# =====================================
# 二、深度--损伤率函数(可按文献自行修改)
# =====================================
def damage_ratio_building(depth):
"""
建筑类资产(居民、工业、服务业等)的深度-损伤率函数 f(d)
注意:这里只给出一个示例形状,实际系数请根据文献或历史数据标定。
"""
d = max(depth, 0.0)
if d <= 0:
return 0.0
elif d <= 0.5:
return 0.10 # 轻度浸水
elif d <= 1.0:
return 0.30
elif d <= 2.0:
return 0.60
else:
return 0.90 # 严重损毁
def damage_ratio_transport(depth):
"""
交通设施的深度-损伤率函数,可略低于建筑或不同形状。
"""
d = max(depth, 0.0)
if d <= 0:
return 0.0
elif d <= 0.3:
return 0.05
elif d <= 1.0:
return 0.20
elif d <= 2.0:
return 0.50
else:
return 0.80
def damage_ratio_municipal(depth):
"""
市政基础设施的损伤率,可以假设对水较敏感。
"""
d = max(depth, 0.0)
if d <= 0:
return 0.0
elif d <= 0.5:
return 0.15
elif d <= 1.5:
return 0.40
elif d <= 3.0:
return 0.75
else:
return 0.95
# 将函数向量化以便对 pandas Series 使用
v_damage_build = np.vectorize(damage_ratio_building)
v_damage_trans = np.vectorize(damage_ratio_transport)
v_damage_muni = np.vectorize(damage_ratio_municipal)
# ==========================================
# 三、读取数据工具函数(简单防错)
# ==========================================
def safe_read_csv(path, desc):
"""
尝试读取 CSV,如果不存在则给出提示并返回 None。
"""
if not os.path.exists(path):
print(f"[提示] 未找到文件:{path} ------ {desc}。请准备好该数据再运行相应部分。")
return None
df = pd.read_csv(path)
print(f"[读取成功] {desc} :{path},共有 {len(df)} 条记录。")
return df
# ===================================
# 四、短期损失:直接 + 间接
# ===================================
def compute_short_term_direct_loss(df_grid):
"""
计算短期直接损失:
对每个 (city, scenario, cell):
L_dir_cell = Σ_k V_{i}^{(k)} * f_k(depth)
然后按 (city, scenario) 聚合。
"""
df = df_grid.copy()
# 各类资产损伤率
df["ratio_res"] = v_damage_build(df["depth"])
df["ratio_ind"] = v_damage_build(df["depth"])
df["ratio_serv"] = v_damage_build(df["depth"])
df["ratio_trans"] = v_damage_trans(df["depth"])
df["ratio_muni"] = v_damage_muni(df["depth"])
# 各类资产损失
df["loss_res"] = df["asset_residential"] * df["ratio_res"]
df["loss_ind"] = df["asset_industrial"] * df["ratio_ind"]
df["loss_serv"] = df["asset_service"] * df["ratio_serv"]
df["loss_trans"] = df["asset_transport"] * df["ratio_trans"]
df["loss_muni"] = df["asset_municipal"] * df["ratio_muni"]
# 单元总直接损失
df["loss_direct_cell"] = df[[
"loss_res", "loss_ind", "loss_serv", "loss_trans", "loss_muni"
]].sum(axis=1)
# 按 city, scenario 聚合
agg_cols = [
"loss_res", "loss_ind", "loss_serv", "loss_trans", "loss_muni", "loss_direct_cell"
]
df_direct = df.groupby(["city", "scenario"], as_index=False)[agg_cols].sum()
print("\n[短期直接损失] 按城市和场景汇总结果预览:")
print(df_direct.head())
# 保存
out_path = os.path.join(OUTPUT_DIR, "short_term_direct_loss_by_city_scenario.csv")
df_direct.to_csv(out_path, index=False)
print(f"[保存] 短期直接损失明细已保存至:{out_path}")
return df_direct
def compute_short_term_indirect_loss(df_service, df_disrupt):
"""
计算短期间接损失:
L_ind(c, s) = Σ_j R_c^{(j)} * T_{c,s}^{(j)}
其中:
df_service: city, sector, daily_output
df_disrupt: city, scenario, sector, days_lost
"""
# 合并两表
df = pd.merge(
df_disrupt,
df_service,
on=["city", "sector"],
how="left"
)
# 如果有缺失的 daily_output,则提示
missing = df[df["daily_output"].isna()]
if not missing.empty:
print("[警告] 部分 (city, sector) 在服务业产出表中缺少 daily_output,请补全:")
print(missing[["city", "scenario", "sector"]].drop_duplicates())
# 计算间接损失
df["loss_indirect"] = df["daily_output"] * df["days_lost"]
df_indirect = df.groupby(["city", "scenario"], as_index=False)["loss_indirect"].sum()
print("\n[短期间接损失] 按城市和场景汇总结果预览:")
print(df_indirect.head())
out_path = os.path.join(OUTPUT_DIR, "short_term_indirect_loss_by_city_scenario.csv")
df_indirect.to_csv(out_path, index=False)
print(f"[保存] 短期间接损失明细已保存至:{out_path}")
return df_indirect
def compute_short_term_expected_loss(df_direct, df_indirect, df_probs):
"""
计算短期预期损失(按城市):
E[L_short(c)] = Σ_s P(c,s) * (L_dir(c,s) + L_ind(c,s))
"""
# 合并 direct 和 indirect
df = pd.merge(
df_direct,
df_indirect,
on=["city", "scenario"],
how="outer"
)
df["loss_indirect"] = df["loss_indirect"].fillna(0.0)
# 合并场景概率
df = pd.merge(
df,
df_probs,
on=["city", "scenario"],
how="left"
)
missing_prob = df[df["prob"].isna()]
if not missing_prob.empty:
print("[警告] 部分 (city, scenario) 缺少场景发生概率 prob,请补全:")
print(missing_prob[["city", "scenario"]].drop_duplicates())
df["prob"] = df["prob"].fillna(0.0)
# 场景层面短期总损失
df["loss_short_scenario"] = df["loss_direct_cell"] + df["loss_indirect"]
# 预期值
df["loss_short_expected_part"] = df["prob"] * df["loss_short_scenario"]
df_short_city = df.groupby("city", as_index=False)[
["loss_short_scenario", "loss_short_expected_part"]
].agg({
"loss_short_scenario": "sum", # 这里是所有场景损失之和(不加权)
"loss_short_expected_part": "sum" # 预期损失
})
df_short_city = df_short_city.rename(columns={
"loss_short_scenario": "loss_short_total_all_scenarios",
"loss_short_expected_part": "loss_short_expected"
})
print("\n[短期预期损失] 按城市汇总结果预览:")
print(df_short_city.head())
out_path = os.path.join(OUTPUT_DIR, "short_term_expected_loss_by_city.csv")
df_short_city.to_csv(out_path, index=False)
print(f"[保存] 各城市短期预期损失已保存至:{out_path}")
return df_short_city, df
# ===================================
# 五、长期损失:农业 + 基建寿命 + 生态
# ===================================
def compute_long_term_agri_loss(df_grid, beta=0.95, T=20):
"""
农业长期损失:
L_agri(c,s) = Σ_{i∈耕地} ΔY_{i,c,s} * β(1-β^T)/(1-β)
其中:
ΔY_{i,c,s} = salt_reduction_rate * farmland_annual_val
"""
df = df_grid.copy()
df_farmland = df[df["is_farmland"] == 1].copy()
if df_farmland.empty:
print("[提示] 栅格数据中无 is_farmland == 1 的记录,农业长期损失为0。")
return pd.DataFrame(columns=["city", "scenario", "L_agri"])
df_farmland["delta_Y"] = df_farmland["salt_reduction_rate"] * df_farmland["farmland_annual_val"]
factor = beta * (1 - beta**T) / (1 - beta)
df_farmland["L_agri_cell"] = df_farmland["delta_Y"] * factor
df_agri = df_farmland.groupby(["city", "scenario"], as_index=False)["L_agri_cell"].sum()
df_agri = df_agri.rename(columns={"L_agri_cell": "L_agri"})
print("\n[长期农业损失] 按城市和场景汇总结果预览:")
print(df_agri.head())
out_path = os.path.join(OUTPUT_DIR, "long_term_agri_loss_by_city_scenario.csv")
df_agri.to_csv(out_path, index=False)
print(f"[保存] 农业长期损失明细已保存至:{out_path}")
return df_agri
def compute_long_term_infra_loss(df_infra, beta=0.95, T=20):
"""
基础设施寿命缩短的长期资本损失:
ΔC_m^{annual} = C_m / T'_m - C_m / T_m
L_infra(c) = Σ_m ΔC_m^{annual} * β(1-β^T)/(1-β)
注意:这里未分场景,默认城市长期处于受海水入侵影响的环境。
若需要按场景区分,可在表中增加 scenario 字段并按需扩展。
"""
df = df_infra.copy()
# 去除非法寿命
df = df[(df["T_original"] > 0) & (df["T_new"] > 0)]
df["delta_C_annual"] = df["cost"] / df["T_new"] - df["cost"] / df["T_original"]
factor = beta * (1 - beta**T) / (1 - beta)
df["L_infra_asset"] = df["delta_C_annual"] * factor
df_infra_city = df.groupby("city", as_index=False)["L_infra_asset"].sum()
df_infra_city = df_infra_city.rename(columns={"L_infra_asset": "L_infra"})
print("\n[长期基础设施损失] 按城市汇总结果预览:")
print(df_infra_city.head())
out_path = os.path.join(OUTPUT_DIR, "long_term_infra_loss_by_city.csv")
df_infra_city.to_csv(out_path, index=False)
print(f"[保存] 基础设施长期损失已保存至:{out_path}")
return df_infra_city
def compute_long_term_eco_loss(df_grid, beta=0.95, T=20):
"""
生态系统服务长期损失:
ΔE_{c,s} = Σ_{i∈湿地/生态敏感区} eco_damage_ratio * eco_annual_val * area
L_eco(c,s) = ΔE_{c,s} * β(1-β^T)/(1-β)
注意:这里为了简单,假定 grid_exposure 中 eco_annual_val 已经是"单元的年生态价值",
不再乘 area。若你的值是单位面积,请自行改为 eco_annual_val * area。
"""
df = df_grid.copy()
# 若只对特定 land_type 计生态损失,可在此筛选,如:
# df = df[df["land_type"].isin(["wetland", "mangrove"])]
df["delta_E"] = df["eco_damage_ratio"] * df["eco_annual_val"]
factor = beta * (1 - beta**T) / (1 - beta)
df["L_eco_cell"] = df["delta_E"] * factor
df_eco = df.groupby(["city", "scenario"], as_index=False)["L_eco_cell"].sum()
df_eco = df_eco.rename(columns={"L_eco_cell": "L_eco"})
print("\n[长期生态损失] 按城市和场景汇总结果预览:")
print(df_eco.head())
out_path = os.path.join(OUTPUT_DIR, "long_term_eco_loss_by_city_scenario.csv")
df_eco.to_csv(out_path, index=False)
print(f"[保存] 生态长期损失明细已保存至:{out_path}")
return df_eco
def compute_long_term_expected_loss(df_agri, df_eco, df_probs, df_infra_city):
"""
计算长期预期损失:
L_long(c,s) = L_agri(c,s) + L_eco(c,s) + (若需要按场景分配的基础设施损失)
E[L_long(c)] = Σ_s P(c,s) * L_long(c,s)
+ 城市维度的基础设施长期损失 L_infra(c)
为简单起见,这里将 L_infra(c) 直接加到长期预期损失中,不区分场景。
"""
# 合并农业和生态(都是 city, scenario)
df = pd.merge(
df_agri,
df_eco,
on=["city", "scenario"],
how="outer"
)
df["L_agri"] = df["L_agri"].fillna(0.0)
df["L_eco"] = df["L_eco"].fillna(0.0)
# 合并场景概率
df = pd.merge(
df,
df_probs,
on=["city", "scenario"],
how="left"
)
df["prob"] = df["prob"].fillna(0.0)
# 场景长期损失
df["L_long_scenario"] = df["L_agri"] + df["L_eco"]
# 预期值
df["L_long_expected_part"] = df["prob"] * df["L_long_scenario"]
df_long_city = df.groupby("city", as_index=False)[
["L_long_scenario", "L_long_expected_part"]
].agg({
"L_long_scenario": "sum",
"L_long_expected_part": "sum"
})
df_long_city = df_long_city.rename(columns={
"L_long_scenario": "L_long_all_scenarios",
"L_long_expected_part": "L_long_expected"
})
# 加入基础设施长期损失
df_long_city = pd.merge(
df_long_city,
df_infra_city,
on="city",
how="left"
)
df_long_city["L_infra"] = df_long_city["L_infra"].fillna(0.0)
df_long_city["L_long_total"] = df_long_city["L_long_expected"] + df_long_city["L_infra"]
print("\n[长期预期损失] 按城市汇总结果预览:")
print(df_long_city.head())
out_path = os.path.join(OUTPUT_DIR, "long_term_expected_loss_by_city.csv")
df_long_city.to_csv(out_path, index=False)
print(f"[保存] 各城市长期预期损失已保存至:{out_path}")
return df_long_city, df
# ===================================
# 六、归一化与综合损失指数计算
# ===================================
def normalize_series_to_01(s):
"""
将一个 Series 线性归一化到 [0,1] 区间。
若所有值相等,则统一设为0.5。
"""
vmin = s.min()
vmax = s.max()
if np.isclose(vmax, vmin):
return pd.Series(0.5, index=s.index)
return (s - vmin) / (vmax - vmin)
def compute_composite_loss_index(df_short_city, df_long_city, df_gdp,
w_short=0.5, w_long=0.5):
"""
计算相对损失指标和综合损失指数:
S_short = E[L_short] / GDP
S_long = L_long_total / GDP
归一化:
S_short* = (S_short - min)/(max - min)
S_long* = (S_long - min)/(max - min)
综合:
C_loss = w_short * S_short* + w_long * S_long*
"""
df = pd.merge(
df_short_city[["city", "loss_short_expected"]],
df_long_city[["city", "L_long_total"]],
on="city",
how="outer"
)
df = pd.merge(
df,
df_gdp,
on="city",
how="left"
)
missing_gdp = df[df["GDP"].isna()]
if not missing_gdp.empty:
print("[警告] 部分城市缺少 GDP,用于归一化时会出问题,请补充:")
print(missing_gdp["city"].unique())
df["GDP"] = df["GDP"].replace(0, np.nan)
df["S_short"] = df["loss_short_expected"] / df["GDP"]
df["S_long"] = df["L_long_total"] / df["GDP"]
df["S_short*"] = normalize_series_to_01(df["S_short"])
df["S_long*"] = normalize_series_to_01(df["S_long"])
df["C_loss"] = w_short * df["S_short*"] + w_long * df["S_long*"]
print("\n[综合损失指数] 结果预览:")
print(df.head())
out_path = os.path.join(OUTPUT_DIR, "composite_loss_index_by_city.csv")
df.to_csv(out_path, index=False)
print(f"[保存] 各城市综合损失指数已保存至:{out_path}")
return df
# ===================================
# 七、可视化:分解 + 对比 + 散点
# ===================================
def plot_short_long_bar(df_short_city, df_long_city):
"""
画出各城市短期与长期预期损失的柱状对比图。
"""
df = pd.merge(
df_short_city[["city", "loss_short_expected"]],
df_long_city[["city", "L_long_total"]],
on="city",
how="inner"
)
df = df.sort_values("loss_short_expected", ascending=False)
x = np.arange(len(df))
width = 0.35
plt.figure(figsize=(10, 5))
plt.bar(x - width/2, df["loss_short_expected"], width=width, label="短期预期损失")
plt.bar(x + width/2, df["L_long_total"], width=width, label="长期预期损失")
plt.xticks(x, df["city"], rotation=45, ha="right")
plt.ylabel("损失金额(单位自定)")
plt.title("各城市短期与长期预期损失对比")
plt.legend()
plt.grid(axis="y", alpha=0.3)
plt.tight_layout()
out_path = os.path.join(OUTPUT_DIR, "short_long_loss_bar.png")
plt.savefig(out_path)
plt.show()
print(f"[保存] 短期与长期损失柱状图:{out_path}")
def plot_loss_composition(df_direct, df_indirect, df_agri, df_eco, df_infra_city):
"""
绘制各城市不同损失构成的堆叠图(示意):
- 短期直接
- 短期间接
- 长期农业
- 长期生态
- 长期基础设施
"""
# 先按城市汇总场景层面的损失
df_dir_city = df_direct.groupby("city", as_index=False)["loss_direct_cell"].sum()
df_ind_city = df_indirect.groupby("city", as_index=False)["loss_indirect"].sum()
df_agri_city = df_agri.groupby("city", as_index=False)["L_agri"].sum()
df_eco_city = df_eco.groupby("city", as_index=False)["L_eco"].sum()
df = df_dir_city.merge(df_ind_city, on="city", how="outer")
df = df.merge(df_agri_city, on="city", how="outer")
df = df.merge(df_eco_city, on="city", how="outer")
df = df.merge(df_infra_city, on="city", how="outer")
df = df.fillna(0.0)
df = df.sort_values("loss_direct_cell", ascending=False)
x = np.arange(len(df))
plt.figure(figsize=(10, 5))
bottom = np.zeros(len(df))
for col, label in [
("loss_direct_cell", "短期直接"),
("loss_indirect", "短期间接"),
("L_agri", "长期农业"),
("L_eco", "长期生态"),
("L_infra", "长期基础设施"),
]:
plt.bar(x, df[col], bottom=bottom, label=label)
bottom += df[col].values
plt.xticks(x, df["city"], rotation=45, ha="right")
plt.ylabel("损失金额(单位自定)")
plt.title("各城市损失构成堆叠图")
plt.legend()
plt.grid(axis="y", alpha=0.3)
plt.tight_layout()
out_path = os.path.join(OUTPUT_DIR, "loss_composition_stacked_bar.png")
plt.savefig(out_path)
plt.show()
print(f"[保存] 各城市损失构成堆叠图:{out_path}")
def plot_short_long_scatter(df_comp):
"""
绘制短期相对损失 vs 长期相对损失的散点图:
横轴:S_short*
纵轴:S_long*
"""
df = df_comp.copy()
plt.figure(figsize=(6, 6))
plt.scatter(df["S_short*"], df["S_long*"], s=60)
for _, row in df.iterrows():
plt.text(row["S_short*"] + 0.01,
row["S_long*"] + 0.01,
row["city"],
fontsize=9)
plt.xlabel("短期损失相对指标 S_short*")
plt.ylabel("长期损失相对指标 S_long*")
plt.title("短期 vs 长期相对损失散点图")
plt.grid(alpha=0.3)
out_path = os.path.join(OUTPUT_DIR, "short_vs_long_scatter.png")
plt.tight_layout()
plt.savefig(out_path)
plt.show()
print(f"[保存] 短期 vs 长期相对损失散点图:{out_path}")
# ===================================
# 八、主流程:按步骤顺序串起来
# ===================================
def main():
# ---------- 1. 读取所有需要的数据 ----------
df_grid = safe_read_csv(PATH_GRID_EXPOSURE, "栅格暴露数据(grid_exposure)")
df_probs = safe_read_csv(PATH_SCENARIO_PROBS, "场景发生概率(scenario_probs)")
df_service = safe_read_csv(PATH_SERVICE_OUTPUT, "服务业日均产出(service_daily_output)")
df_disrupt = safe_read_csv(PATH_SERVICE_DISRUPT, "服务业停摆时间(service_disruption_days)")
df_infra = safe_read_csv(PATH_INFRA_LIFE, "基础设施寿命数据(infra_lifetime)")
df_gdp = safe_read_csv(PATH_CITY_GDP, "城市GDP数据(city_gdp)")
if df_grid is None or df_probs is None:
print("\n[终止] 关键数据缺失(grid_exposure 或 scenario_probs),无法计算问题2。")
return
# ---------- 2. 短期损失:直接 ----------
df_direct = compute_short_term_direct_loss(df_grid)
# ---------- 3. 短期损失:间接 ----------
if df_service is not None and df_disrupt is not None:
df_indirect = compute_short_term_indirect_loss(df_service, df_disrupt)
else:
print("\n[提示] 缺少服务业数据或停摆时间,将短期间接损失视为0。")
# 构造一个全0的表,与 df_direct 城市/场景对应
df_indirect = df_direct[["city", "scenario"]].copy()
df_indirect["loss_indirect"] = 0.0
# ---------- 4. 短期预期损失 ----------
df_short_city, df_short_detail = compute_short_term_expected_loss(
df_direct, df_indirect, df_probs
)
# ---------- 5. 长期损失:农业 ----------
df_agri = compute_long_term_agri_loss(df_grid, beta=0.95, T=20)
# ---------- 6. 长期损失:生态 ----------
df_eco = compute_long_term_eco_loss(df_grid, beta=0.95, T=20)
# ---------- 7. 长期损失:基础设施 ----------
if df_infra is not None:
df_infra_city = compute_long_term_infra_loss(df_infra, beta=0.95, T=20)
else:
print("\n[提示] 缺少基础设施寿命数据,将长期基础设施损失视为0。")
# 构造空表,以防后续合并出错
df_infra_city = pd.DataFrame(columns=["city", "L_infra"])
# ---------- 8. 长期预期损失 ----------
df_long_city, df_long_detail = compute_long_term_expected_loss(
df_agri, df_eco, df_probs, df_infra_city
)
# ---------- 9. 综合损失指数 ----------
if df_gdp is None:
print("\n[提示] 缺少GDP数据,不能做相对指标和综合指数,只保留绝对损失。")
return
df_comp = compute_composite_loss_index(
df_short_city,
df_long_city,
df_gdp,
w_short=0.5,
w_long=0.5
)
# ---------- 10. 可视化展示 ----------
# 短期 vs 长期预期绝对损失
plot_short_long_bar(df_short_city, df_long_city)
# 各类损失构成堆叠图
plot_loss_composition(df_direct, df_indirect, df_agri, df_eco, df_infra_city)
# 短期 vs 长期相对损失散点
plot_short_long_scatter(df_comp)
print("\n[完成] 问题2:短期与长期损失评估计算和可视化已完成。")
if __name__ == "__main__":
main()后续都在"数模加油站"......