Opencv(十五) : 图像梯度处理

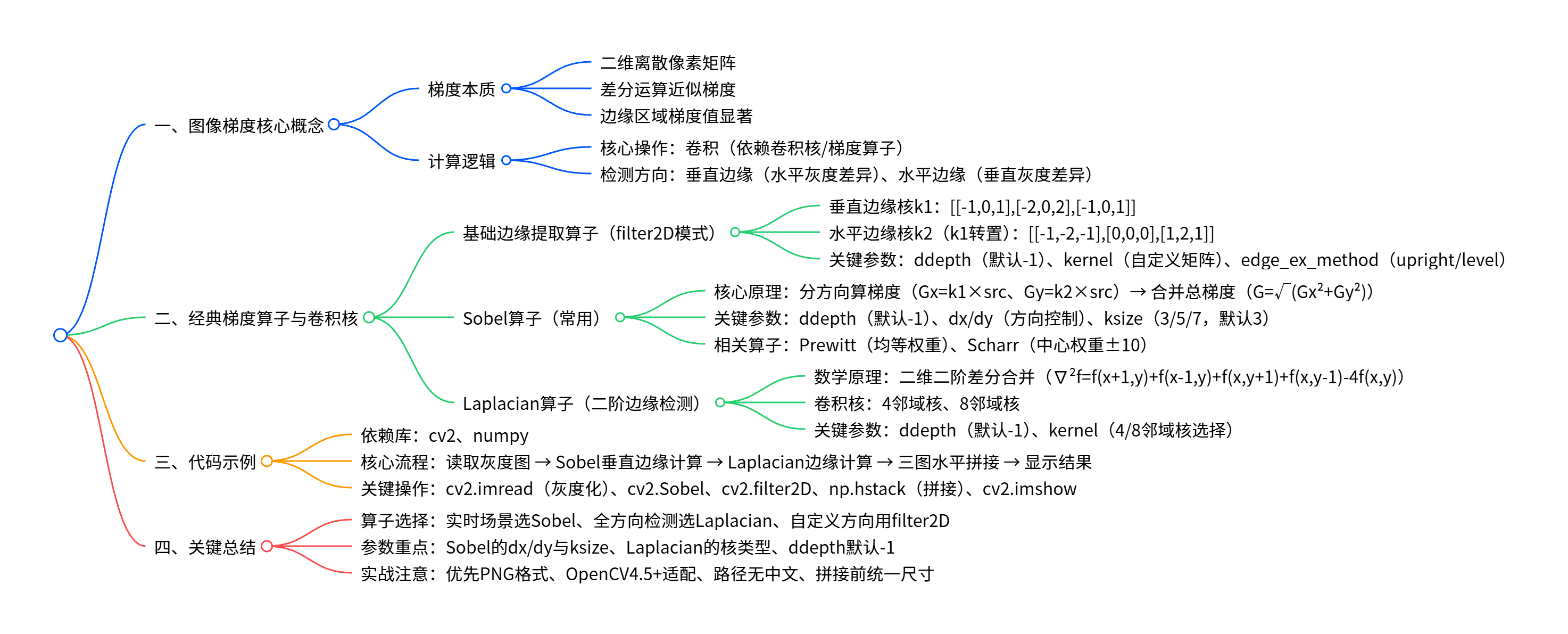
文章目录

思维导图
前言
- 一、图像梯度核心概念
- - [1.1 梯度的本质](#1.1 梯度的本质)
  - [1.2 梯度的计算逻辑](#1.2 梯度的计算逻辑)
- 二、经典梯度算子与卷积核（重点）
- - [2.1 基础边缘提取算子（filter2D模式）](#2.1 基础边缘提取算子（filter2D模式）)
  - - [2.1.1 垂直边缘提取核（k1）](#2.1.1 垂直边缘提取核（k1）)
    - [2.1.2 水平边缘提取核（k2）](#2.1.2 水平边缘提取核（k2）)
    - [2.1.3 filter2D模式参数说明](#2.1.3 filter2D模式参数说明)
  - [2.2 Sobel算子（最常用梯度算子）](#2.2 Sobel算子（最常用梯度算子）)
  - - [2.2.1 核心原理](#2.2.1 核心原理)
    - [2.2.2 Sobel模式参数说明](#2.2.2 Sobel模式参数说明)
    - [2.2.3 相关算子对比](#2.2.3 相关算子对比)
  - [2.3 Laplacian算子（二阶边缘检测）](#2.3 Laplacian算子（二阶边缘检测）)
  - - [2.3.1 数学原理](#2.3.1 数学原理)
    - [2.3.2 卷积核形式](#2.3.2 卷积核形式)
    - [2.3.3 Laplacian模式参数说明](#2.3.3 Laplacian模式参数说明)
- [三、代码示例](#三、代码示例)
- - - 核心代码示例
- 四、关键总结

思维导图

前言

在计算机视觉中，图像梯度是提取边缘、分析像素灰度变化的核心工具。本文基于图像梯度处理核心知识，聚焦原理拆解、经典算子、参数配置与实战步骤，剔除冗余内容，直击技术要点

一、图像梯度核心概念

1.1 梯度的本质

图像是二维离散像素矩阵，无法直接计算连续函数的导数，因此用差分运算近似梯度------梯度反映像素灰度值在空间上的变化率，边缘区域因像素值突变，差分结果（梯度）会显著异于平坦区域，这是梯度提取边缘的核心原理。

1.2 梯度的计算逻辑

基础操作 ：通过卷积实现梯度计算，核心是卷积核（梯度算子）------不同卷积核对应不同方向、不同精度的梯度提取。
核心方向 ：
- 垂直边缘：检测像素在水平方向（左右）的灰度差异；
- 水平边缘：检测像素在垂直方向（上下）的灰度差异。

二、经典梯度算子与卷积核（重点）

梯度算子的核心是卷积核设计，不同算子通过调整核内权重，实现边缘检测精度、抗噪性的平衡。以下是PDF中重点讲解的4类算子：

2.1 基础边缘提取算子（filter2D模式）

通过自定义卷积核，直接对图像进行卷积运算，提取指定方向边缘，是最基础的梯度处理方式。

2.1.1 垂直边缘提取核（k1）

卷积核形式：
k 1 = $- 1 0 1 - 2 0 2 - 1 0 1$ k1=\begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1\end{bmatrix} k1= −1−2−1000121

原理：核内左右列权重相反（左负右正），通过计算"当前列左右两侧像素的加权差分"，放大垂直方向的灰度突变（边缘）。
示例：若原图某列像素为[247, 0, 196]，经k1卷积后，差分结果绝对值过大时会被截断（如-290→0，930→255），最终突出垂直边缘。

2.1.2 水平边缘提取核（k2）

将垂直边缘核转置，即可得到水平边缘提取核：
k 2 = $- 1 - 2 - 1 0 0 0 1 2 1$ k2=\begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1\end{bmatrix} k2= −101−202−101

原理：核内上下行权重相反（上负下正），计算"当前行上下两侧像素的加权差分"，提取水平边缘。

2.1.3 filter2D模式参数说明

在梯度处理组件中，选择filter_method=filter2D时，关键参数含义：

参数名	含义
`ddepth`	目标图像的深度，设为-1时表示与输入图像深度一致（常用默认值）
`kernel`	自定义卷积核，需输入单通道浮点矩阵（如上述k1、k2）
`edge_ex_method`	边缘检测方向：`upright`（垂直）、`level`（水平）

2.2 Sobel算子（最常用梯度算子）

Sobel算子是基础边缘提取算子的优化版，通过"分方向计算梯度+合并总梯度"，提升边缘检测的鲁棒性，是工业场景中的首选。

2.2.1 核心原理

分方向计算梯度 ：
- 水平梯度（Gx）：用垂直边缘核k1与原图卷积，捕捉垂直边缘，公式： G x = k 1 × s r c G_x = k1 × src Gx=k1×src；
- 垂直梯度（Gy）：用水平边缘核k2与原图卷积，捕捉水平边缘，公式： G y = k 2 × s r c G_y = k2 × src Gy=k2×src；
计算总梯度 ：合并两个方向的梯度，得到边缘的综合强度，公式： G = G x 2 + G y 2 G=\sqrt{G_x^2 + G_y^2} G=Gx2+Gy2 （实际为简化计算，也可用 ∣ G x ∣ + ∣ G y ∣ |G_x| + |G_y| ∣Gx∣+∣Gy∣近似）。

2.2.2 Sobel模式参数说明

选择filter_method=Sobel时，关键参数需重点配置：

参数名	含义
`ddepth`	目标图像深度，默认-1
`dx/dy`	梯度方向控制： - `dx=1, dy=0`：计算x方向（水平）一阶导数（垂直边缘）； - `dx=0, dy=1`：计算y方向（垂直）一阶导数（水平边缘）； - 禁止同时设为1（结果无意义）
`ksize`	Sobel算子大小，可选3、5、7，默认3（3×3核兼顾速度与精度）

2.2.3 相关算子对比

PDF中提及Sobel的两类替代算子，可根据场景选择：

Prewitt算子 ：权重均等，抗噪性略弱于Sobel，核形式：
k = $- 1 0 1 - 1 0 1 - 1 0 1$ k=\begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1\end{bmatrix} k= −1−1−1000111
Scharr算子 ：权重更大（中心列权重±10），边缘检测更灵敏，核形式：
k = $- 3 0 3 - 10 0 10 - 3 0 3$ k=\begin{bmatrix} -3 & 0 & 3 \\ -10 & 0 & 10 \\ -3 & 0 & 3\end{bmatrix} k= −3−10−30003103

2.3 Laplacian算子（二阶边缘检测）

与Sobel（一阶导数）不同，Laplacian算子基于二阶导数------数学中"一阶导数极值处，二阶导数为0"，因此通过二阶差分可直接定位边缘，且对所有方向边缘（水平、垂直、斜向）均敏感。

2.3.1 数学原理

二维二阶差分公式 ：
对像素 f ( x , y ) f(x,y) f(x,y)，x和y方向的二阶差分分别为：
∂ 2 f ∂ x 2 = f ( x + 1 , y ) + f ( x − 1 , y ) − 2 f ( x , y ) \frac{\partial^2 f}{\partial x^2}=f(x+1,y)+f(x-1,y)-2f(x,y) ∂x2∂2f=f(x+1,y)+f(x−1,y)−2f(x,y)
∂ 2 f ∂ y 2 = f ( x , y + 1 ) + f ( x , y − 1 ) − 2 f ( x , y ) \frac{\partial^2 f}{\partial y^2}=f(x,y+1)+f(x,y-1)-2f(x,y) ∂y2∂2f=f(x,y+1)+f(x,y−1)−2f(x,y)
合并二阶差分 ：
总二阶差分（Laplacian值）为两个方向之和：
∇ 2 f ( x , y ) = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) \nabla^2 f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) ∇2f(x,y)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)

2.3.2 卷积核形式

从二阶差分公式中提取权重，得到Laplacian的两类核心：

基础核（4邻域） ：仅考虑上下左右像素，核形式：
k = $0 1 0 1 - 4 1 0 1 0$ k=\begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0\end{bmatrix} k= 0101−41010
扩展核（8邻域） ：包含斜对角像素，边缘检测更全面，核形式：
k = $1 1 1 1 - 8 1 1 1 1$ k=\begin{bmatrix} 1 & 1 & 1 \\ 1 & -8 & 1 \\ 1 & 1 & 1\end{bmatrix} k= 1111−81111

2.3.3 Laplacian模式参数说明

选择filter_method=Laplacian时，参数较简单：

ddepth：目标图像深度，默认-1；
kernel：直接使用上述4邻域或8邻域核（无需额外配置方向参数，因对所有方向边缘敏感）。

三、代码示例

核心代码示例

python 复制代码

import cv2
import numpy as np

if __name__ == "__main__":
    # 读取输入图片
    path = "shudu.png"
    image_np = cv2.imread(path, cv2.IMREAD_GRAYSCALE)

    # 1. Sobel算子（垂直边缘）
    sobel_x = cv2.Sobel(image_np, ddepth=-1, dx=1, dy=0, ksize=3)
    # 2. Laplacian算子（4邻域核）
    laplacian_kernel = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]], dtype=np.float32)
    laplacian_result = cv2.filter2D(image_np, ddepth=-1, kernel=laplacian_kernel)

    # 将三张图水平拼接（需确保尺寸一致）
    combined = np.hstack((image_np, sobel_x, laplacian_result))
    # 显示合并后的图
    cv2.imshow("Original + Sobel X + Laplacian", combined)

    cv2.waitKey(0)
    cv2.destroyAllWindows()

输出结果维

四、关键总结

算子选择原则 ：
- 快速验证/实时场景：选Sobel（3×3核），平衡速度与精度；
- 全方向边缘检测：选Laplacian（8邻域核），适合复杂纹理；
- 自定义边缘方向：用filter2D+自定义核，灵活度最高。
参数配置重点 ：
- Sobel的dx/dy决定边缘方向，ksize越大抗噪性越强；
- Laplacian的核选择（4/8邻域）决定边缘覆盖范围；
- ddepth默认设-1，避免图像深度不匹配导致的错误。
实战注意 ：
- 图片格式：优先用原生PNG，避免后缀修改；
- 代码运行：确保OpenCV版本适配