2025年11月21日14:02
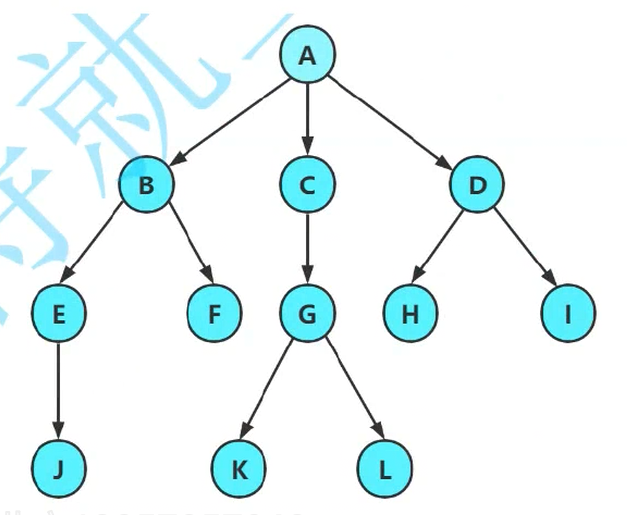
概念:
节点的度:方法:看儿子有几个,或者看子数有几个。
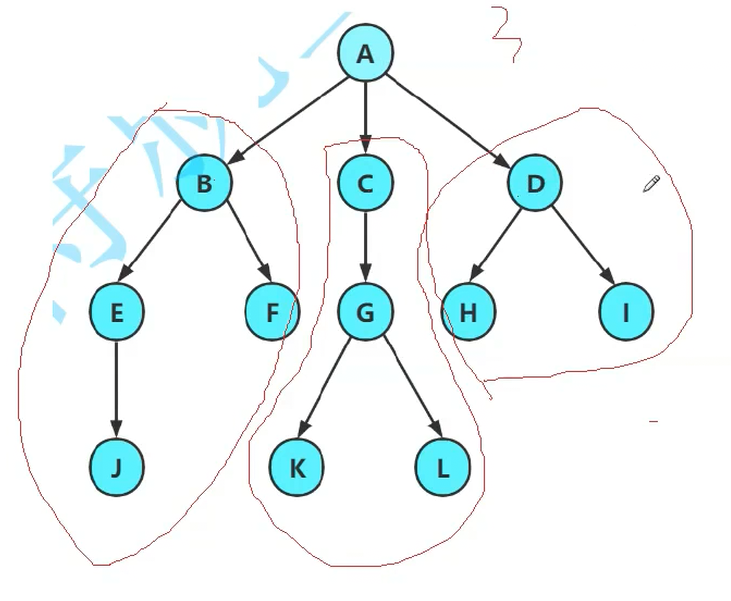
如图,A有3个子树。
**叶子结点(终端结点):**度=0的结点;没有孩子,如;J,K,L,H,I
非终端节点(分支节点 ):中间度不为0的结点**(** A是不是分支节点)
父(双亲)节点和孩子(子)节点:B是E的父节点,E是B的子节点。一个结点可能既是双亲结点,又是子节点,该概念具有相对性。
兄弟(默认亲兄第)结点 :如E和F。(对双亲的原始祖先高度没有要求?)
堂兄弟结点:双亲在同一层的结点互为堂兄弟。
树的度:度最大结点的度是整棵树的度。
**树的层次:**一层一层往下走。可以把A看作是第0层,也可以把她当作是第一层。一般的:A是第1层被当作。
树的深(高)度:最大层数。
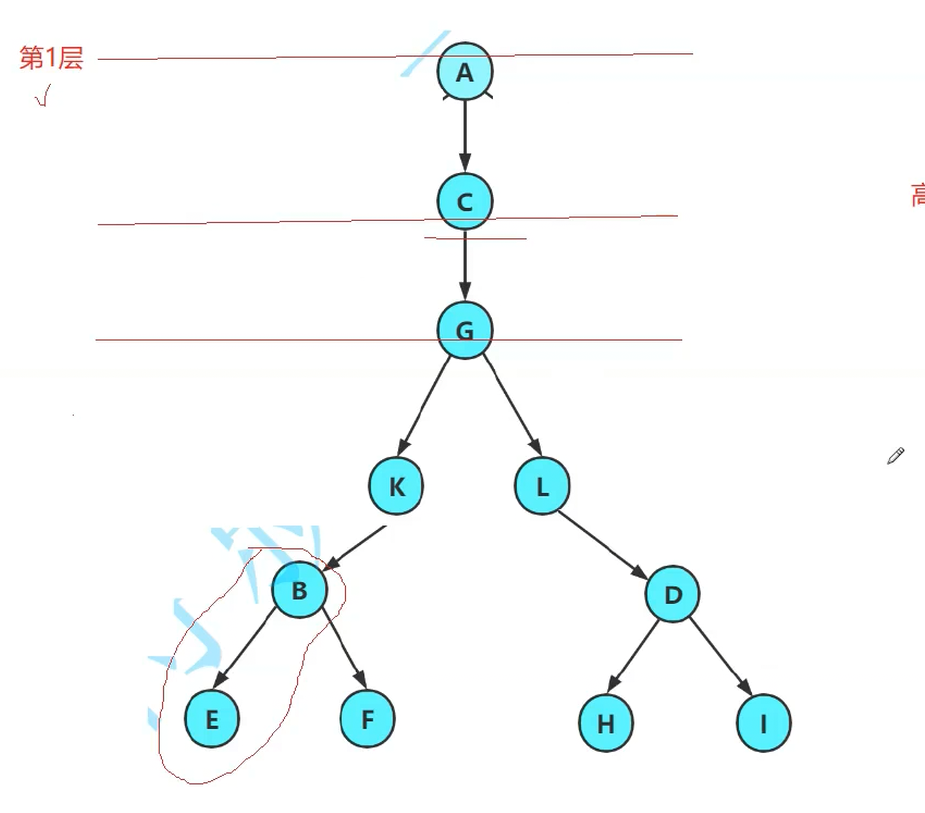
如图,有6层,最大高度为6.
这里没有严格的定义,如果A记为0层,从第0层开始,这棵树的高度应该是5.(事实上我们喜欢从1开始)
为什么我们喜欢从1开始:
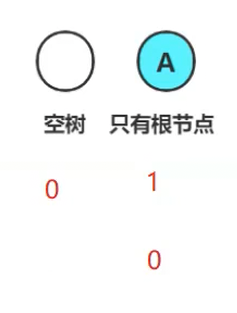
这里涉及到空树和根节点树的区分:如果我们定义A为1,那么跟结点树就是1,空树理所应当是0.(而不必设置为-1)
既然从1开始好,为什么会出现从0开始的说法:因为数组就是从0开始的。有些人就喜欢统一方法;
那么,为什么数组下标必须从0开始呢
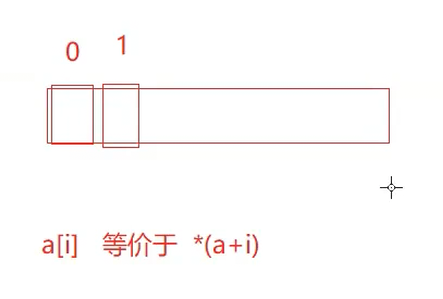
从0开始是不可避免地,数组的名称是数组首元素的地址,这点不可改变,所以根据数组的指针本质:如图:表示必须从0开始。
祖先结点:从当前结点向上一切直系血亲都可以称之为祖先。旁系不算。
子孙节点:该节点以下所有结点
**森林:**多棵树就可以被称之为森林(注意这个是一个单独的数据结构;以后的并查集就是森林)
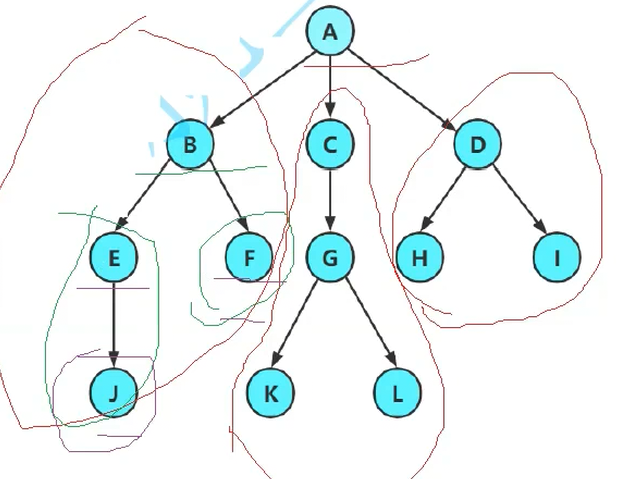
一棵树的定义是递归定义的
一棵树有根+N颗子树两个部分组成。N>=0
A有A这个根+子树BCD构成,B有B这个根和EF这两个子树构成。依此类推。递归本质。
递归解决问题又可以称之为分治。
注意:区分线性表,树是非线性数据结构,特点是复杂。非一对一关系。
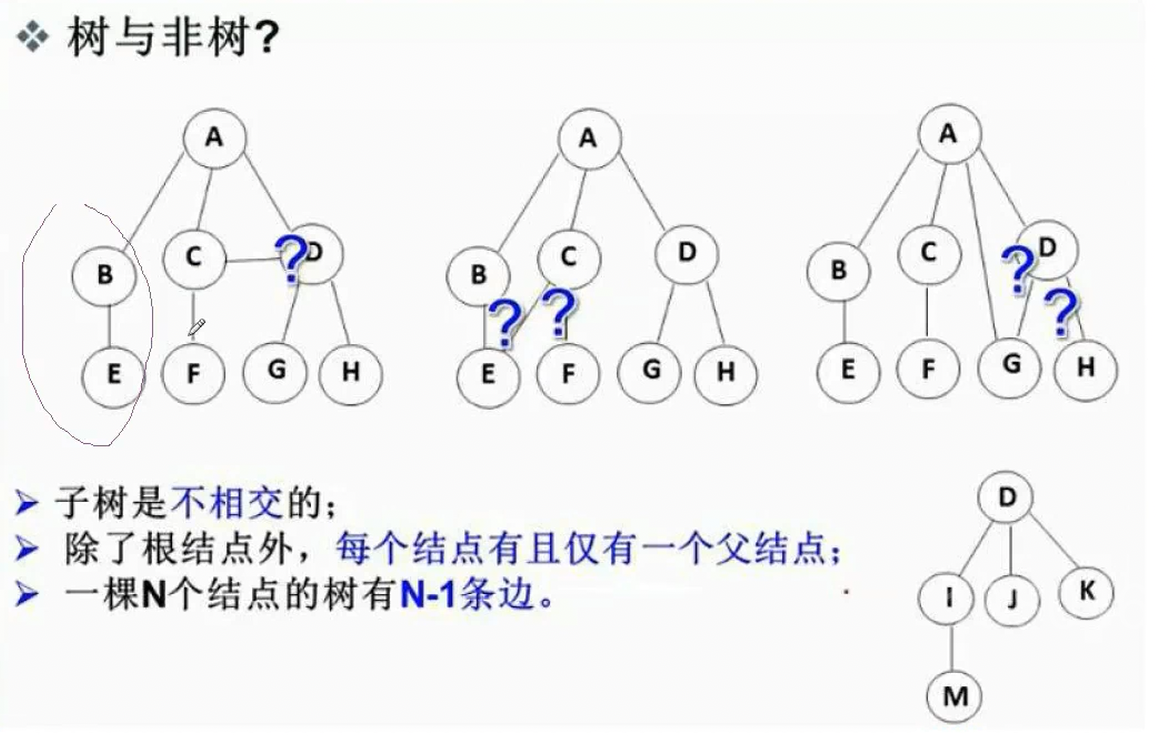
根和子树之间不能有关联。如果有联系:那么就叫图
如何定义一棵树?
不怎么好的方法:

数组和顺序表
比较好的方法
左孩子右兄弟表示法

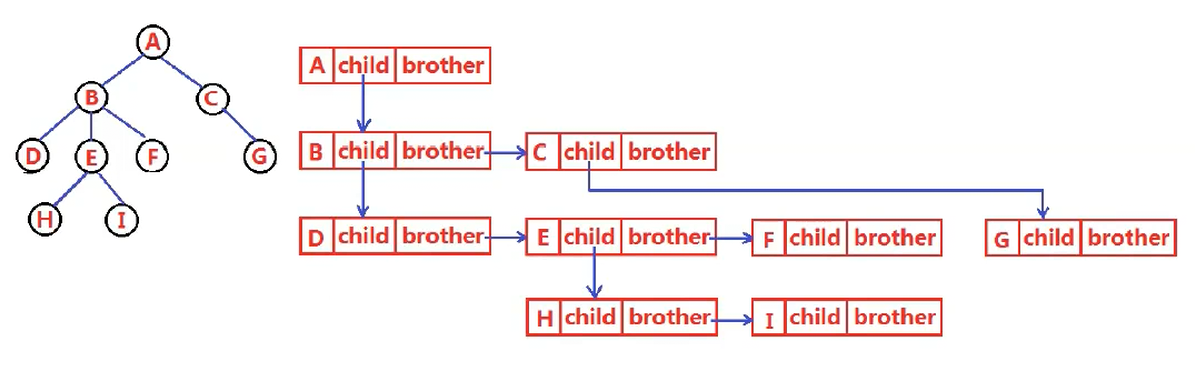
每一个根节点,我只需要找到它的大儿子,随后我就能用大儿子的rightbrother指针找到其他所有儿子。

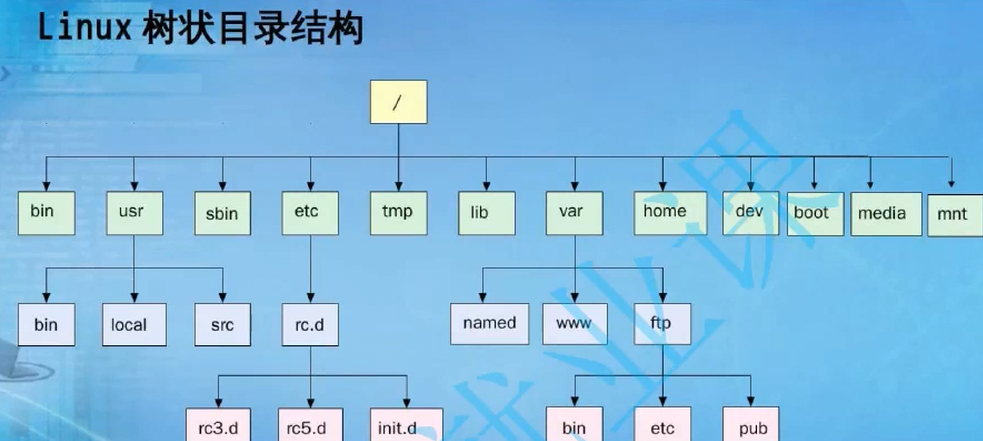
生活中的树:windows整个系统就是一篇森林
C是一颗树,D是一棵树,树下有文件夹,文件夹下面有小文件夹,在下面有文件。以此类推。
有时我们会将其称为目录树:就像这样