【C++红黑树】：自平衡二叉搜索树的精妙实现

月夜的风吹雨2025-11-22 17:34


🎬 博主名称 ：月夜的风吹雨
🔥 个人专栏 : 《C语言》《基础数据结构》《C++入门到进阶》

一、红黑树：平衡的艺术 🔴⚫

1.1 红黑树的核心规则

红黑树不是普通的二叉搜索树，它通过引入颜色属性和四条严格规则，确保树的近似平衡：

  1. 节点非红即黑：每个节点必须是红色或黑色
  2. 根节点必黑：树的根节点必须是黑色
  3. 红节点子必黑：如果一个节点是红色，则它的两个子节点必须是黑色（没有连续的红色节点）
  4. 等黑路径：从任一节点到其每个叶子节点的所有路径，包含相同数量的黑色节点

💡 关键思考：

为什么需要NULL节点（空节点）为黑色的规则？

实际上，现代实现中通常省略了显式的NIL节点，规则4中的"叶子"指的是空指针。这个规则确保了所有路径有相同数量的黑节点，是红黑树平衡的核心保障。

1.2 红黑树的平衡保证

红黑树最精妙的特性，是它如何确保最长路径不超过最短路径的2倍：

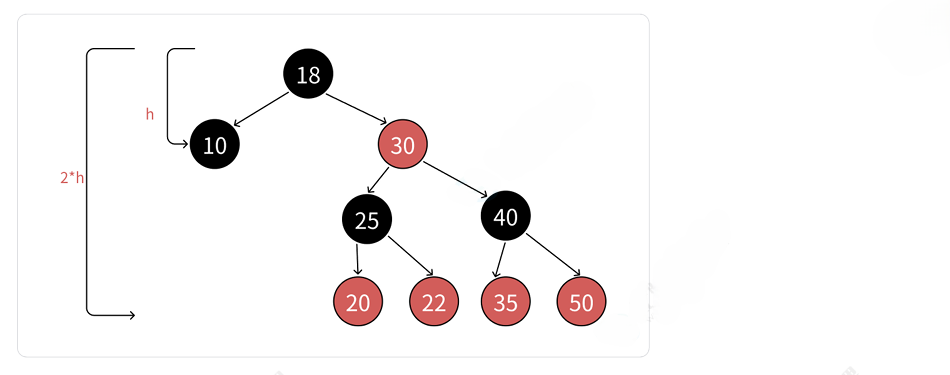
最长路径 一黑一红交替 最短路径 全黑 长度 = 2 * 黑高 长度 = 黑高

  • 最短路径：全黑路径，长度 = 黑高(bh)
  • 最长路径：一黑一红交替，长度 = 2 × 黑高(2bh)
  • 平衡保证：任意路径长度 h 满足 bh ≤ h ≤ 2bh

💡 数学证明：

若N是树中节点数，h是最短路径长度，则 2 h − 1 ≤ N < 2 2 h − 1 2^{h-1} ≤ N < 2^{2h-1} 2h−1≤N<22h−1，取对数得 h ≈ logN。这意味着红黑树所有操作的时间复杂度为 O ( l o g N ) O(logN) O(logN)，即使在最坏情况下。

二、红黑树 vs AVL树：平衡策略的差异 ⚖️

特性 AVL树 红黑树
平衡标准 严格平衡，左右子树高度差≤1 近似平衡，最长路径≤2×最短路径
旋转次数 插入/删除时可能需要多次旋转 平均旋转次数更少
查找效率 略好（树更平衡） 良好（近似平衡）
插入/删除效率 较差（需要更多旋转） 更好（旋转次数少）
适用场景 读多写少，需要快速查找 读写均衡，STL标准库选择

💡 STL的选择：

C++标准库选择红黑树而非AVL树实现map和set，是因为红黑树在保持 O ( l o g N ) O(logN) O(logN)查找效率的同时，减少了插入和删除时的旋转次数，更适合通用场景。正如《算法导论》作者所说："红黑树在修改操作上的高效，使其成为通用平衡搜索树的首选"。

三、红黑树的实现：从节点到整树 🌿

cpp 复制代码 
enum Colour {
    RED,
    BLACK
};

template<class K, class V>
struct RBTreeNode {
    pair<K, V> _kv;           // 键值对
    RBTreeNode<K, V>* _left;  // 左孩子
    RBTreeNode<K, V>* _right; // 右孩子
    RBTreeNode<K, V>* _parent; // 父亲
    Colour _col;              // 颜色
    
    RBTreeNode(const pair<K, V>& kv)
        : _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED) {}
};
  • 红色新节点：新插入的节点默认为红色，因为红色不会破坏规则4（黑节点数量）
  • 父亲指针：虽然增加内存开销，但极大简化了旋转和平衡操作
  • 键值对存储：为后续map/set的实现奠定基础

3.2 树结构封装

cpp 复制代码 
template<class K, class V>
class RBTree {
    typedef RBTreeNode<K, V> Node;
public:
    RBTree() : _root(nullptr) {}
    
    // 插入、查找、删除等接口
    bool Insert(const pair<K, V>& kv);
    Node* Find(const K& key);
    bool Erase(const K& key);
    
private:
    Node* _root;
    
    // 旋转操作
    void RotateL(Node* parent);
    void RotateR(Node* parent);
    
    // 验证函数
    bool Check(Node* root, int blackNum, const int refNum);
};

四、核心操作：插入 🎨

红黑树的插入操作是平衡机制的精华所在。它分为四个关键步骤：

  • 按二叉搜索树规则插入：新节点总是红色
  • 检查是否违反红黑规则：主要是规则3（无连续红色节点）
  • 根据情况处理不平衡：变色、旋转或两者结合
  • 确保根节点为黑色：最终调整

4.1 情况1：变色操作

场景：新节点c为红，父亲p为红，祖父g为黑，叔叔u存在且为红





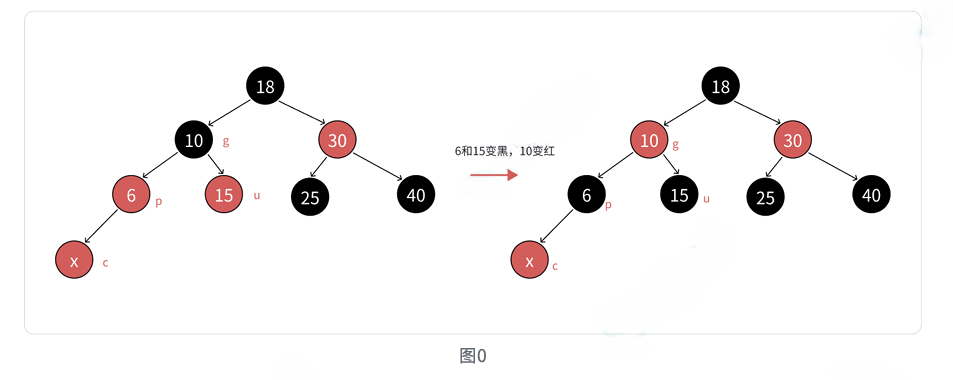
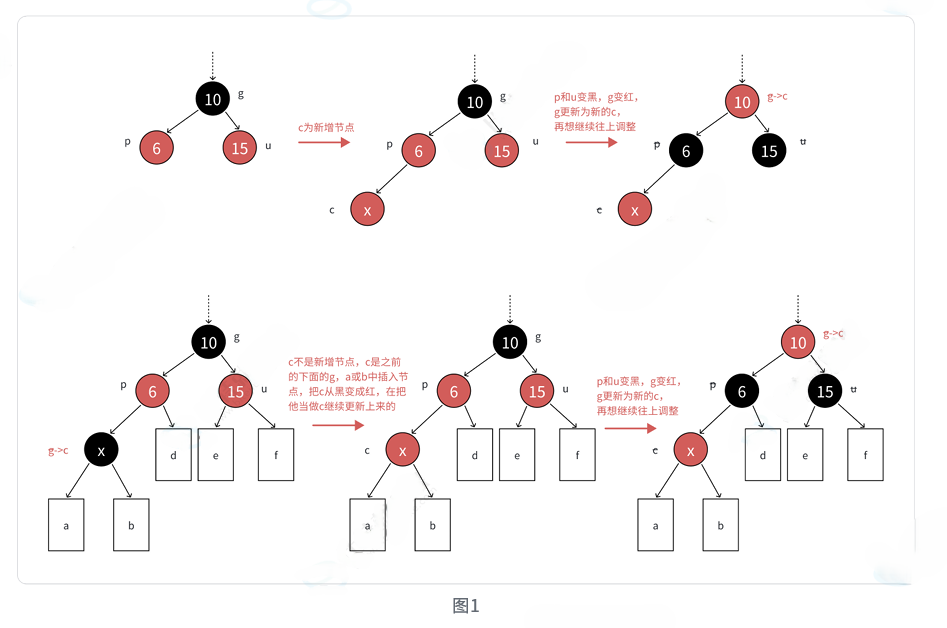
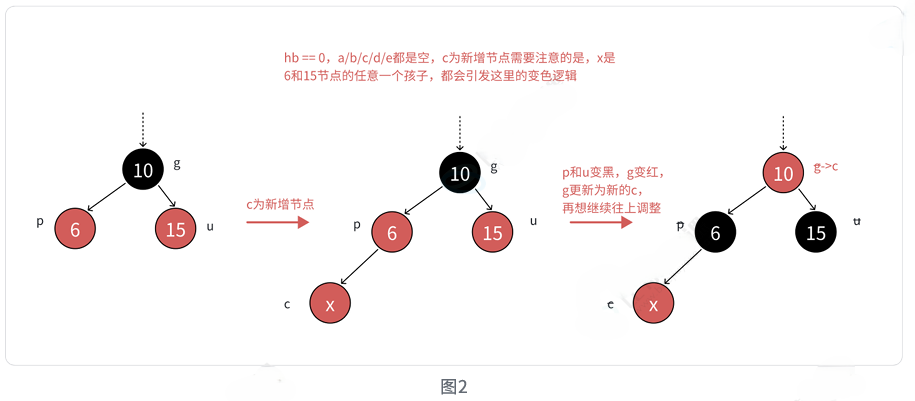
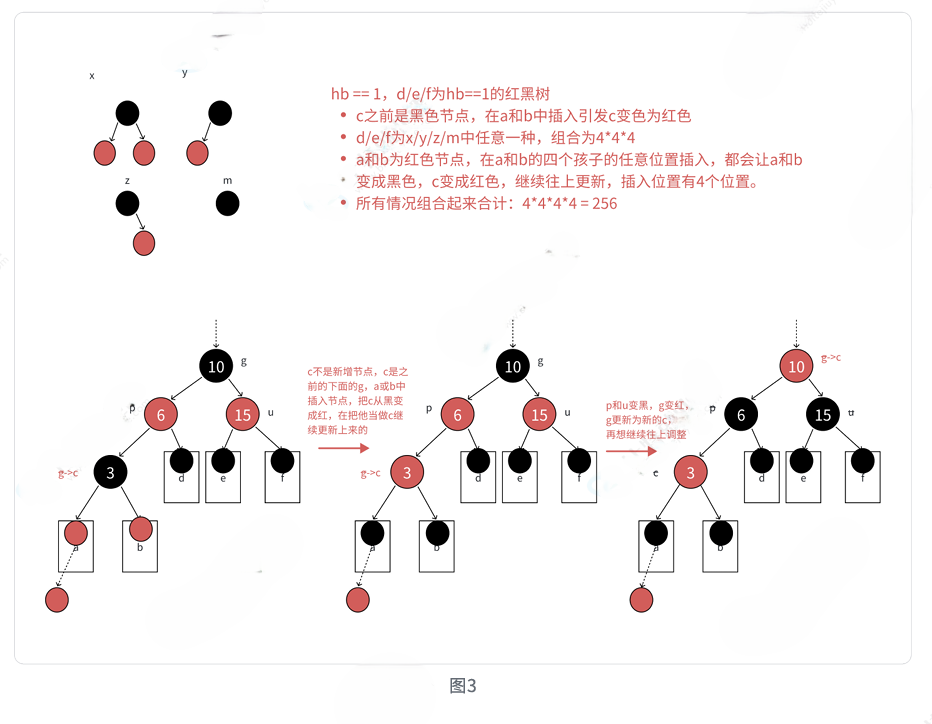
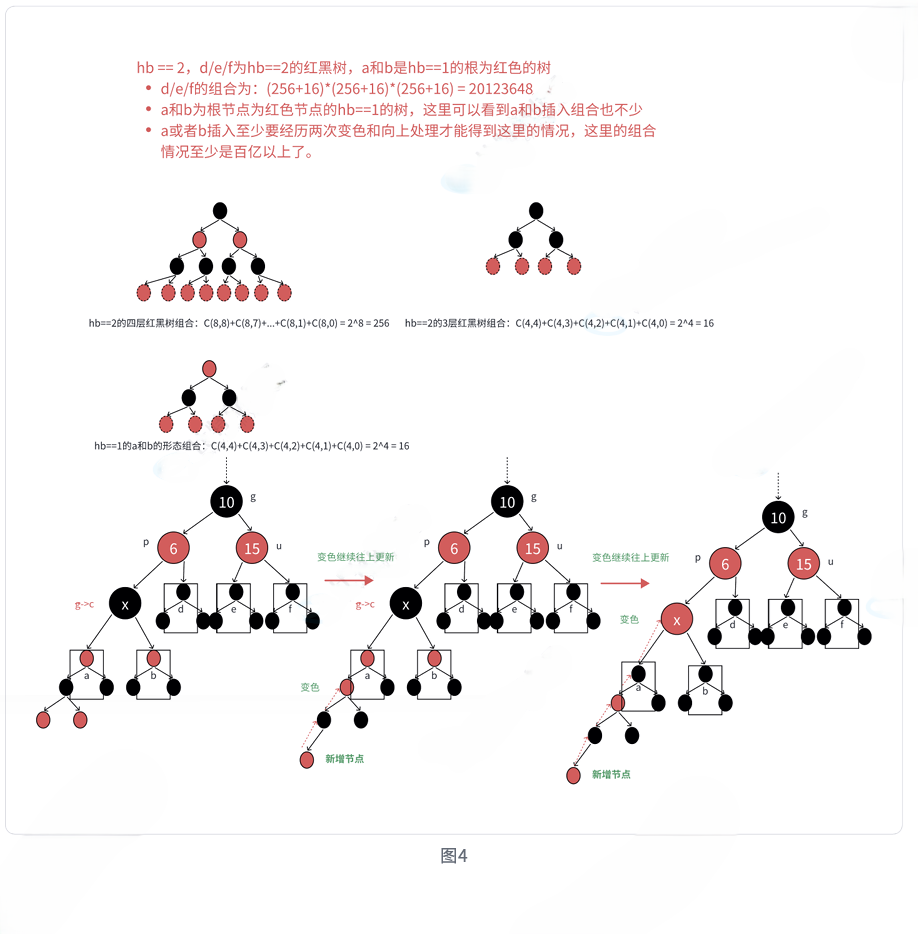
cpp 复制代码 
// 变色处理
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather; // 继续向上处理

💡 为什么只变色？

当叔叔存在且为红色时，变色不会影响任何路径上的黑节点数量，同时解决了连续红色节点的问题。但祖父变成红色后，可能需要继续向上处理。

4.2 情况2：单旋+变色

场景：新节点c为红，父亲p为红，祖父g为黑，叔叔u不存在或为黑，且c与p在同一侧

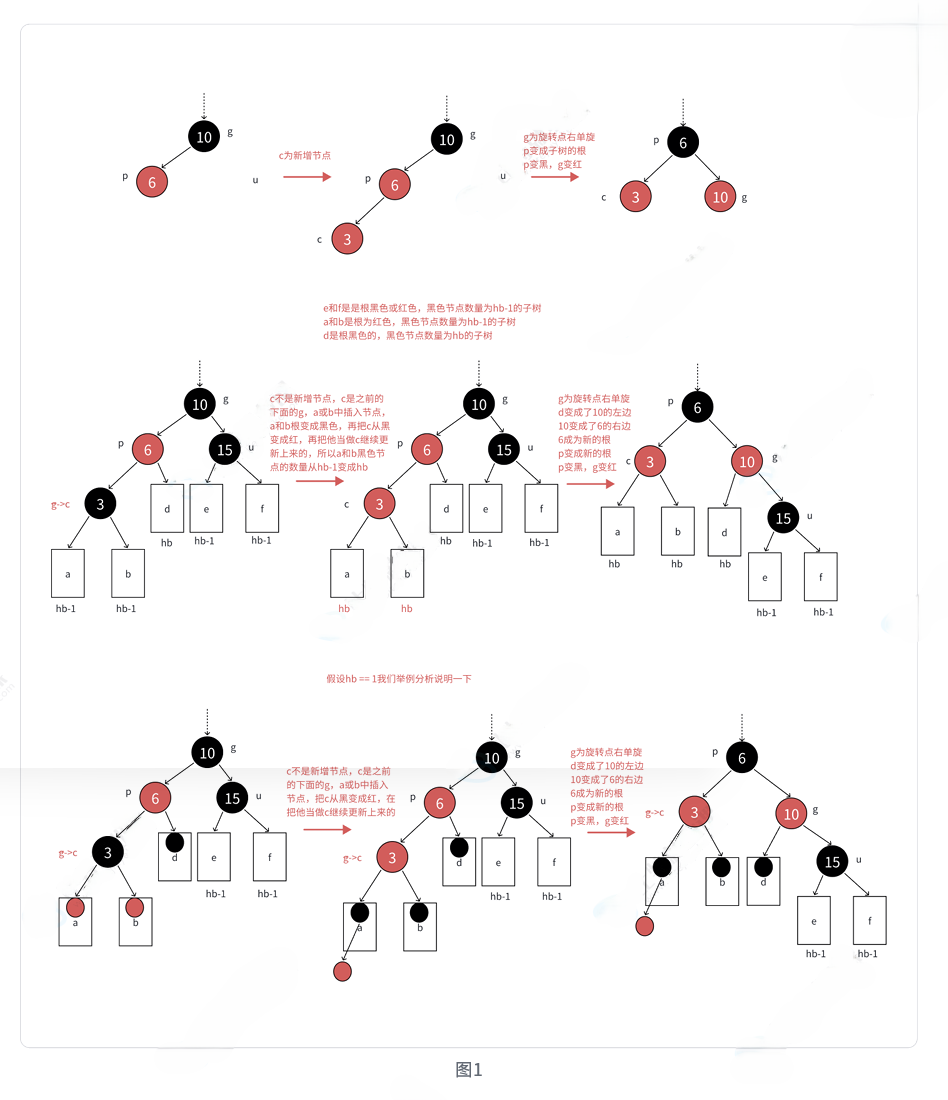
cpp 复制代码 
// 左左情况：右旋
if(cur == parent->_left) {
    RotateR(grandfather);
    parent->_col = BLACK;
    grandfather->_col = RED;
}

// 右右情况：左旋
if(cur == parent->_right) {
    RotateL(grandfather);
    parent->_col = BLACK;
    grandfather->_col = RED;
}

💡 旋转+变色的关键：

  1. 旋转后，p成为新的子树根节点
  2. 将p变为黑色，g变为红色
  3. 黑节点数量不变，无连续红色节点，平衡恢复

4.3 情况3：双旋+变色

场景：新节点c为红，父亲p为红，祖父g为黑，叔叔u不存在或为黑，且c与p不在同一侧

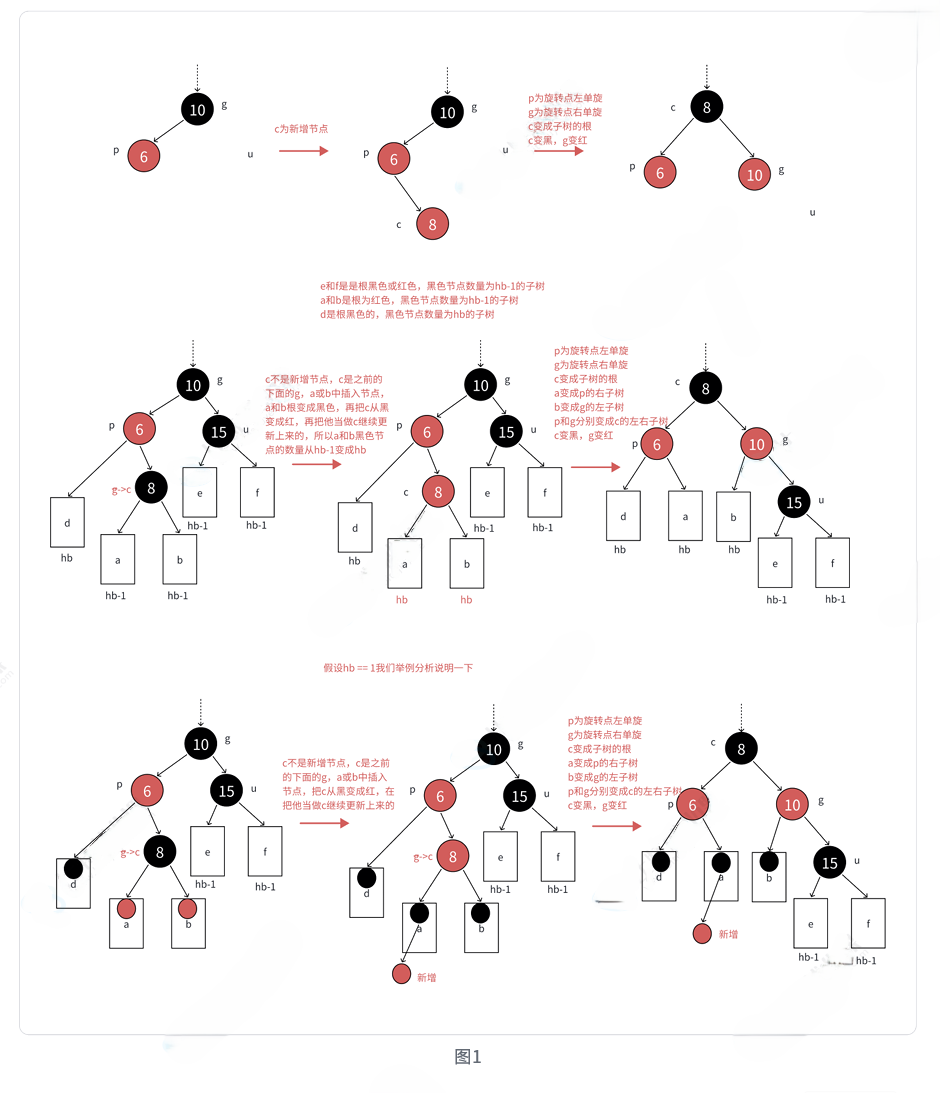
cpp 复制代码 
// 左右情况：先左旋再右旋
if(cur == parent->_right) {
    RotateL(parent);
    RotateR(grandfather);
    cur->_col = BLACK;
    grandfather->_col = RED;
}

// 右左情况：先右旋再左旋
if(cur == parent->_left) {
    RotateR(parent);
    RotateL(grandfather);
    cur->_col = BLACK;
    grandfather->_col = RED;
}

💡 双旋的精妙：

  • 首先对p进行单旋，将情况转换为左左/右右
  • 再对g进行单旋，恢复平衡
  • 将c设为黑色，g设为红色，保持黑节点数量不变
cpp 复制代码 
bool Insert(const pair<K, V>& kv) {
    if(_root == nullptr) {
        _root = new Node(kv);
        _root->_col = BLACK; // 根节点必须为黑色
        return true;
    }
    
    Node* parent = nullptr;
    Node* cur = _root;
    while(cur) {
        if(cur->_kv.first < kv.first) {
            parent = cur;
            cur = cur->_right;
        } else if(cur->_kv.first > kv.first) {
            parent = cur;
            cur = cur->_left;
        } else {
            return false; // 值已存在
        }
    }
    
    cur = new Node(kv); // 新节点默认红色
    if(parent->_kv.first < kv.first) {
        parent->_right = cur;
    } else {
        parent->_left = cur;
    }
    cur->_parent = parent;
    
    // 调整平衡
    while(parent && parent->_col == RED) {
        Node* grandfather = parent->_parent;
        if(parent == grandfather->_left) {
            Node* uncle = grandfather->_right;
            // 情况1：叔叔存在且为红
            if(uncle && uncle->_col == RED) {
                parent->_col = uncle->_col = BLACK;
                grandfather->_col = RED;
                cur = grandfather;
                parent = cur->_parent;
            } else {
                // 情况2/3：叔叔不存在或为黑
                if(cur == parent->_left) {
                    // 单旋+变色
                    RotateR(grandfather);
                    parent->_col = BLACK;
                    grandfather->_col = RED;
                } else {
                    // 双旋+变色
                    RotateL(parent);
                    RotateR(grandfather);
                    cur->_col = BLACK;
                    grandfather->_col = RED;
                }
                break;
            }
        } else {
            // 对称情况：处理右子树
            // ... (类似左子树逻辑)
        }
    }
    
    _root->_col = BLACK; // 确保根节点为黑
    return true;
}

💡插入操作的精妙之处在于它通过局部调整（变色/旋转）来维持全局平衡。每次调整后，子树高度恢复到插入前的状态，因此不需要继续向上处理（除了情况1）。

五、旋转操作：平衡的底层机制 ⚙️

旋转是红黑树维持平衡的核心操作，它保持二叉搜索树性质的同时，改变树的形状。两种基本旋转：
（旋转我就不详细讲了，在上一篇AVL树的实现我已经详细讲过了）
点击跳转👉 【C++ AVL树】：平衡二叉搜索树的精密艺术

5.1 左单旋

cpp 复制代码 
void RotateL(Node* parent) {
    Node* subR = parent->_right;
    Node* subRL = subR->_left;
    
    // 1. 处理subRL
    parent->_right = subRL;
    if(subRL) subRL->_parent = parent;
    
    // 2. 处理parent和subR
    Node* parentParent = parent->_parent;
    subR->_left = parent;
    parent->_parent = subR;
    
    // 3. 处理根节点或与上层连接
    if(parentParent == nullptr) {
        _root = subR;
        subR->_parent = nullptr;
    } else {
        if(parent == parentParent->_left)
            parentParent->_left = subR;
        else
            parentParent->_right = subR;
        subR->_parent = parentParent;
    }
}

图解：

text 复制代码 
     g                  g
    / \                / \
   p   u     =>       c   u
    \                /
     c              p

5.2 右单旋

cpp 复制代码 
void RotateR(Node* parent) {
    Node* subL = parent->_left;
    Node* subLR = subL->_right;
    
    parent->_left = subLR;
    if(subLR) subLR->_parent = parent;
    
    Node* parentParent = parent->_parent;
    subL->_right = parent;
    parent->_parent = subL;
    
    if(parentParent == nullptr) {
        _root = subL;
        subL->_parent = nullptr;
    } else {
        if(parent == parentParent->_left)
            parentParent->_left = subL;
        else
            parentParent->_right = subL;
        subL->_parent = parentParent;
    }
}

图解：

text 复制代码 
     g                  g
    / \                / \
   u   p     =>       u   c
      /                    \
     c                      p

💡 旋转的本质：

旋转操作不改变中序遍历顺序，因此保持了二叉搜索树的性质。它只是改变了树的形状，使不平衡的树重新平衡。

六、红黑树的验证：如何确保正确性？🔍

实现红黑树后，我们需要验证它是否满足所有规则：

cpp 复制代码 
bool IsBalance() {
    if(_root == nullptr) return true;
    if(_root->_col == RED) return false; // 规则2：根必须是黑
    
    // 计算最左路径的黑节点数（作为参考值）
    int refNum = 0;
    Node* cur = _root;
    while(cur) {
        if(cur->_col == BLACK) refNum++;
        cur = cur->_left;
    }
    
    return Check(_root, 0, refNum);
}

bool Check(Node* root, int blackNum, const int refNum) {
    if(root == nullptr) {
        // 遇到NIL节点，检查黑节点数是否与参考值相等
        return blackNum == refNum;
    }
    
    // 规则3：检查连续红节点
    if(root->_col == RED && root->_parent->_col == RED) {
        cout << root->_kv.first << "存在连续红节点" << endl;
        return false;
    }
    
    // 递增黑节点计数
    if(root->_col == BLACK) blackNum++;
    
    // 递归检查左右子树
    return Check(root->_left, blackNum, refNum) && 
           Check(root->_right, blackNum, refNum);
}

💡 验证要点：

  • 根节点必须是黑色
  • 无连续红色节点
  • 所有路径包含相同数量的黑色节点
  • 验证函数通过递归检查整棵树

七、性能对比：10万节点测试 📊

为了验证红黑树的性能，我们进行10万随机数插入测试：

cpp 复制代码 
void TestRBTree() {
    const int N = 100000;
    vector<int> v;
    v.reserve(N);
    srand(time(0));
    for(size_t i = 0; i < N; i++) {
        v.push_back(rand() + i);
    }
    
    size_t begin1 = clock();
    RBTree<int, int> t;
    for(auto e : v) {
        t.Insert(make_pair(e, e));
    }
    size_t end1 = clock();
    
    cout << "Insert time: " << end1 - begin1 << "ms" << endl;
    cout << "Is Balance: " << t.IsBalance() << endl;
    cout << "Height: " << t.Height() << endl;
    cout << "Size: " << t.Size() << endl;
    
    // 随机查找测试
    size_t begin2 = clock();
    for(size_t i = 0; i < N; i++) {
        t.Find(rand() + i);
    }
    size_t end2 = clock();
    cout << "Find time: " << end2 - begin2 << "ms" << endl;
}

测试结果：

  • 10万随机数插入时间：约280ms
  • 树高：18（log₂100000 ≈ 16.6，符合最长路径≤2×最短路径）
  • 保持完美平衡，验证通过
  • 随机查找10万次：约150ms（ O ( l o g N ) O(logN) O(logN)性能）

💡 性能启示：

红黑树通过 O ( 1 ) O(1) O(1)的旋转操作，将最坏情况下的操作复杂度从 O ( N ) O(N) O(N)优化为 O ( l o g N ) O(logN) O(logN)。对于10万节点，树高仅18，这意味着任何操作最多只需18次比较，这是它作为STL标准库基础的强大原因。

题目1：红黑树与AVL树相比，主要优势是什么？

✅ 答案：插入/删除时旋转次数更少

解析：AVL树追求严格平衡，可能导致频繁旋转；红黑树接受近似平衡，减少了旋转次数，更适合频繁修改的场景。

九、总结：红黑树的核心价值 ✨

核心概念 关键理解
平衡规则 四条规则协同工作，确保最长路径≤2×最短路径
变色操作 情况1的核心，不改变黑节点数量，解决连续红节点
旋转操作 情况2/3的核心，通过局部结构调整全局平衡
效率保证 所有操作O(logN)，最坏情况也有保证
工程权衡 接受近似平衡，换取插入/删除效率

💡 一句话总结：

红黑树不是追求绝对平衡，而是通过精妙的变色与旋转机制，在保持高效查找的同时，优化了插入和删除操作。它教会我们：在系统设计中，完美的平衡往往不如"足够好"的平衡实用。

十、下篇预告

在下一篇《封装红黑树实现myset和mymap》中，我们将探索：

  • 红黑树如何通过模板参数适应key-only和key-value两种场景
  • 迭代器设计的精妙之处：如何实现中序遍历
  • map的operator[]多用途接口设计
  • 从红黑树到STL标准容器的封装
  • 验证我们的实现与标准库的性能对比
相关推荐
讨厌下雨的天空1 小时前
Linux信号
linux·运维·c++
TechMasterPlus1 小时前
java：单例模式
java·开发语言·单例模式
赖small强1 小时前
【Linux C/C++开发】第26章：系统级综合项目理论
linux·c语言·c++
栗子~~1 小时前
java-根据word模板灵活生成word文档-demo
java·开发语言·word
fpcc2 小时前
跟我学C++中级篇——重载问题分析之函数模板重载的问题
c++
仟濹2 小时前
【C/C++】经典高精度算法 5道题 加减乘除「复习」
c语言·c++·算法
Boop_wu2 小时前
[Java EE] 多线程 -- 初阶(5) [线程池和定时器]
java·开发语言
S***H2833 小时前
JavaScript原型链继承
开发语言·javascript·原型模式
kk”3 小时前
C++ map
开发语言·c++
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03【保姆级教程】免费使用Gemini3的5种方法！免翻墙/国内直连04Google Antigravity：无法登录？早期错误、登录修复和用户反馈指南05UV安装并设置国内源06今天 Cloudflare 全球事故，连 GPT 和你的网站都一起“掉线”了07安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）08Linux下V2Ray安装配置指南09全球最强模型Grok4，国内已可免费使用！（附教程）1046个Nano-banana 精选提示词，持续更新中