深度学习实践 - 使用卷积神经网络的手写数字识别

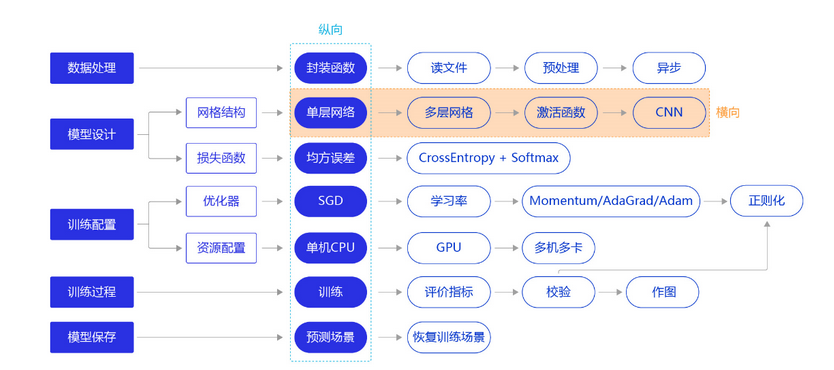
使用简单的单层神经网络（线性回归）来做手写数字识别效果并不好，图片是二维的，我们将特征都展平成一维了，按咱们的优化路线，从网络层面进行调整，使用多层神经网络，并且尝试加入卷积层

bash 复制代码

#数据处理部分之前的代码，保持不变
import os
import random
import paddle
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image

import gzip
import json

# 定义数据集读取器
def load_data(mode='train'):

    # 加载数据
    datafile = './work/mnist.json.gz'
    print('loading mnist dataset from {} ......'.format(datafile))
    data = json.load(gzip.open(datafile))
    print('mnist dataset load done')

    # 读取到的数据区分训练集，验证集，测试集
    train_set, val_set, eval_set = data

    # 数据集相关参数，图片高度IMG_ROWS, 图片宽度IMG_COLS
    IMG_ROWS = 28
    IMG_COLS = 28

    if mode == 'train':
        # 获得训练数据集
        imgs, labels = train_set[0], train_set[1]
    elif mode == 'valid':
        # 获得验证数据集
        imgs, labels = val_set[0], val_set[1]
    elif mode == 'eval':
        # 获得测试数据集
        imgs, labels = eval_set[0], eval_set[1]
    else:
        raise Exception("mode can only be one of ['train', 'valid', 'eval']")

    #校验数据
    imgs_length = len(imgs)
    assert len(imgs) == len(labels), \
          "length of train_imgs({}) should be the same as train_labels({})".format(
                  len(imgs), len(labels))

    # 定义数据集每个数据的序号， 根据序号读取数据
    index_list = list(range(imgs_length))
    # 读入数据时用到的batchsize
    BATCHSIZE = 100
    
    # 定义数据生成器
    def data_generator():
        if mode == 'train':
            random.shuffle(index_list)
        imgs_list = []
        labels_list = []
        for i in index_list:
            img = np.array(imgs[i]).astype('float32')
            label = np.array(labels[i]).astype('float32')
            # 在使用卷积神经网络结构时，uncomment 下面两行代码，全连接神经网络输入是一维的，卷积神经网络这里输入是二维的数组，再加一个批次id（单张图片也填加上，所以固定为1）
            img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
            label = np.reshape(labels[i], [1]).astype('float32')
            
            imgs_list.append(img) 
            labels_list.append(label)
            if len(imgs_list) == BATCHSIZE:
                yield np.array(imgs_list), np.array(labels_list)
                imgs_list = []
                labels_list = []

        # 如果剩余数据的数目小于BATCHSIZE，
        # 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
        if len(imgs_list) > 0:
            yield np.array(imgs_list), np.array(labels_list)

    return data_generator
# 定义激活函数
def sigmoid(x):
    # 直接返回sigmoid函数
    return 1. / (1. + np.exp(-x))
 
# param:起点，终点，间距
x = np.arange(-8, 8, 0.2)
y = sigmoid(x)
plt.plot(x, y)
plt.show()


import paddle.nn.functional as F
from paddle.nn import Linear

# 定义多层全连接神经网络
class MNIST_FULL(paddle.nn.Layer):
    def __init__(self):
        super(MNIST_FULL, self).__init__()
        # 定义两层全连接隐含层，输出维度是10，当前设定隐含节点数为10，可根据任务调整
        self.fc1 = Linear(in_features=784, out_features=10)
        self.fc2 = Linear(in_features=10, out_features=10)
        # 定义一层全连接输出层，输出维度是1
        self.fc3 = Linear(in_features=10, out_features=1)
    
    # 定义网络的前向计算，隐含层激活函数为sigmoid，输出层不使用激活函数
    def forward(self, inputs):
        # inputs = paddle.reshape(inputs, [inputs.shape[0], 784])
        outputs1 = self.fc1(inputs)
        outputs1 = F.sigmoid(outputs1)
        outputs2 = self.fc2(outputs1)
        outputs2 = F.sigmoid(outputs2)
        outputs_final = self.fc3(outputs2)
        return outputs_final

# 定义 SimpleNet 网络结构
import paddle
from paddle.nn import Conv2D, MaxPool2D, Linear
import paddle.nn.functional as F
# 多层卷积神经网络实现
class MNIST_CONV(paddle.nn.Layer):
     def __init__(self):
         super(MNIST_CONV, self).__init__()
         
         # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
         self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)
         # 定义池化层，池化核的大小kernel_size为2，池化步长为2
         self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)
         # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
         self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)
         # 定义池化层，池化核的大小kernel_size为2，池化步长为2
         self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)
         # 定义一层全连接层，输出维度是1
         self.fc = Linear(in_features=980, out_features=1)
         
    # 定义网络前向计算过程，卷积后紧接着使用池化层，最后使用全连接层计算最终输出
    # 卷积层激活函数使用Relu，全连接层不使用激活函数
     def forward(self, inputs):
         x = self.conv1(inputs)
         x = F.relu(x)
         x = self.max_pool1(x)
         x = self.conv2(x)
         x = F.relu(x)
         x = self.max_pool2(x)
         x = paddle.reshape(x, [x.shape[0], -1])
         x = self.fc(x)
         return x

飞桨卷积算子对应的API是paddle.nn.Conv2D，用户可以直接调用API进行计算，也可以在此基础上修改。Conv2D名称中的"2D"表明卷积核是二维的，多用于处理图像数据。类似的，也有Conv3D可以用于处理视频数据（图像的序列）。

复制代码

class paddle.nn.Conv2D (in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, padding_mode='zeros', weight_attr=None, bias_attr=None, data_format='NCHW')

常用的参数如下：

复制代码

in_channels(int) - 输入图像的通道数。
out_channels(int) - 卷积核的个数，和输出特征图通道数相同，相当于上文中的CoutC_{out}Cout。
kernel_size(int|list|tuple) - 卷积核大小，可以是整数，比如3，表示卷积核的高和宽均为3 ；或者是两个整数的list，例如[3,2]，表示卷积核的高为3，宽为2。
stride(int|list|tuple，可选) - 步长大小，可以是整数，默认值为1，表示垂直和水平滑动步幅均为1；或者是两个整数的list，例如[3,2]，表示垂直滑动步幅为3，水平滑动步幅为2。
padding(int|list|tuple|str，可选) - 填充大小，可以是整数，比如1，表示竖直和水平边界填充大小均为1；或者是两个整数的list，例如[2,1]，表示竖直边界填充大小为2，水平边界填充大小为1。

输入数据维度[N,Cin,Hin,Win]，输出数据维度[N,out_channels,Hout,Wout]，权重参数w的维度[out_channels,Cin,filter_size_h,filter_size_w]，偏置参数b的维度是[out_channels]。注意，即使输入只有一张灰度图片[Hin,Win]，也需要处理成四个维度的输入向量[1,1,Hin,Win]。

bash 复制代码

#网络结构部分之后的代码，保持不变
def train(model):
    model.train()
    #调用加载数据的函数，获得MNIST训练数据集
    train_loader = load_data('train')
    # 使用SGD优化器，learning_rate设置为0.01
    opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
    # 训练5轮
    EPOCH_NUM = 10
    # MNIST图像高和宽
    IMG_ROWS, IMG_COLS = 28, 28
    loss_list = []
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            #准备数据
            images, labels = data
            images = paddle.to_tensor(images)
            labels = paddle.to_tensor(labels)
            
            #前向计算的过程
            predicts = model(images)
            
            #计算损失，取一个批次样本损失的平均值
            loss = F.square_error_cost(predicts, labels)
            avg_loss = paddle.mean(loss)

            #每训练200批次的数据，打印下当前Loss的情况
            if batch_id % 200 == 0:
                loss = avg_loss.numpy()[0]
                loss_list.append(loss)
                print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, loss))
            
            #后向传播，更新参数的过程
            avg_loss.backward()
            # 最小化loss,更新参数
            opt.step()
            # 清除梯度
            opt.clear_grad()

    #保存模型参数
    paddle.save(model.state_dict(), 'mnist.pdparams')
    return loss_list

model = MNIST_CONV()
loss_list = train(model)

bash 复制代码

def plot(loss_list):
    plt.figure(figsize=(10,5))
    
    freqs = [i for i in range(len(loss_list))]
    # 绘制训练损失变化曲线
    plt.plot(freqs, loss_list, color='#e4007f', label="Train loss")
    
    # 绘制坐标轴和图例
    plt.ylabel("loss", fontsize='large')
    plt.xlabel("freq", fontsize='large')
    plt.legend(loc='upper right', fontsize='x-large')
    
    plt.show()

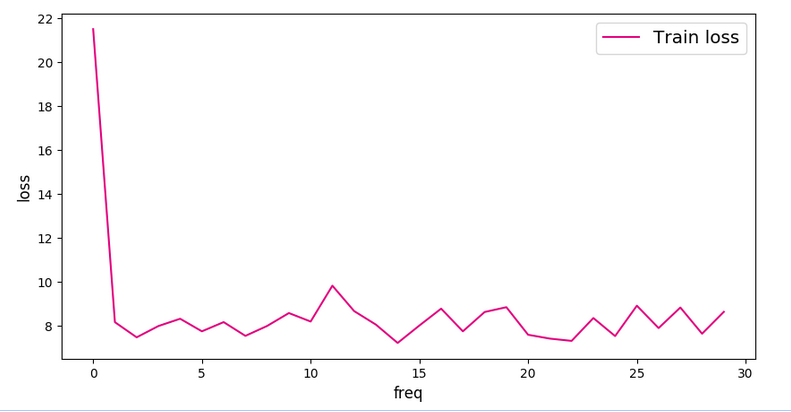
plot(loss_list)

最终作图对比全连接和卷积神经网络的Loss如下：

全连接：

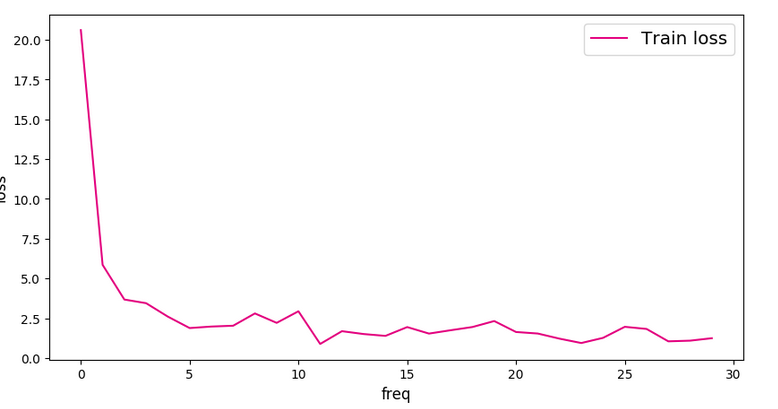
卷积神经网络：

还可以在测试集上进行测试：

bash 复制代码

# 定义预测过程
def cal_pre(predicts, lables):
    i = 0
    correct_num = 0
    for pre_num in predicts:
        if pre_num.numpy().astype('int32') == lables[i]:
            print(pre_num, lables[i])
            correct_num += 1
        i = i + 1
    print("correct_num:", correct_num)

def test():
    model = MNIST_CONV()
    params_file_path = 'mnist.pdparams'
    # 加载模型参数
    param_dict = paddle.load(params_file_path)
    model.load_dict(param_dict)
    # 灌入数据
    model.eval()
    #test_loader = load_data('eval')
    for batch_id, data in enumerate(test_loader()):
            print("batch_id:", batch_id)
            #准备数据
            images, labels = data
            images = paddle.to_tensor(images)
            labels = paddle.to_tensor(labels)
            
            #前向计算的过程
            predicts = model(images)
            print(predicts.shape)
            cal_pre(predicts, labels)
            
            #print("predicts:", predicts)
            #print("lables:", labels)
            break
            #print("predicts:", predicts)
            #print("lables:", labels)
            #print("本次预测的数字是", predicts.numpy().astype('int32'))
test()

这里观察了第一个批次的数据预测正确率是40%