【CUDA笔记】03 CUDA GPU 架构与一般的程序优化思路（下）

引言

前一节主要从 GPU 的结构方面介绍 Cuda 程序的优化思路，这一节将主要从内存结构方面介绍优化思路。

本节主要是对应视频课程的第 2 节与第 4 节

1.GPU 的内存结构

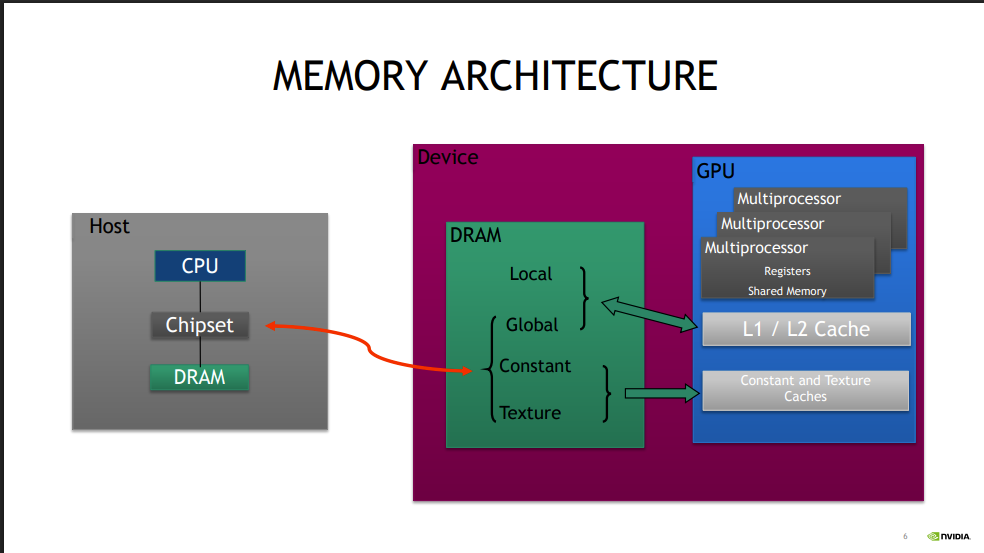
Local storage

每个线程有自己的 local storage

通常为寄存器（有由编译器管理）

Shared memory / L1

同一个 block 中的线程可以共享同一个 shared memory 的空间

延时非常低

吞吐量较高数 TB/秒（取决于访问模式和 bank 冲突情况）

一般容量较小（48KB， 64KB， 96KB...）

L2

所有对 global memory 的访问都问经过 L2，包括从 CPU 到 GPU 或者 GPU 到 CPU 的数据拷贝过程

GLobalMemory

所有的线程都可以访问到（包括 CPU 这一侧的线程）

访问延迟较高

吞吐量 最高可达约 900 GB/秒（基于 Volta 架构的 V100 芯片）

容量大可达数十倍 GB

2.Shared Memory

2.1 什么是共享内存，这一设计起到什么作用？

（1）共享内存 是一种位于 GPU 芯片上的高速内存，允许同一个 block 内的所有线程之间共享数据。

（2）它主要用于减少全局内存访问次数 ，从而提升性能。相比于全局内存，共享内存的访问延迟显著更低，通常只需要几个时钟周期。这使得它非常适合用于频繁访问的小块数据。

（3）使用 __shared__ 关键字声明共享内存变量。

（4）这些变量在每个 block 内独立分配，并且只对该 block 内的线程可见

（5）代码设计上，可以借助这一层级来优化对 Global Memory的访问模式。

2.2 共享内存如何使用

声明

复制代码

__shared__ int sharedData[256];  // 每个 block 都有自己的 sharedData 数组

2.3 同步机制

因为不同的线程可对同一个内存空间进行读写操作，所以必然要有同步机制。

需要使用 __syncthreads() 函数来同步

例如，在一个线程向共享内存写入数据后，可能要等到其他所有线程都执行完写操作才继续执行

复制代码

__shared__ int temp[256];
if (threadIdx.x < 256) {
    temp[threadIdx.x] = globalData[threadIdx.x]; // 从全局内存加载到共享内存
}
__syncthreads();  // 确保所有线程都完成了加载

2.4 应用场景

1. 矩阵乘法

在矩阵乘法中，可以利用共享内存来缓存子矩阵块，减少对全局内存的访问次数。
这种方法被称为"tile-based"方法，能够显著提升计算效率。

2. 直方图计算

当计算图像直方图时，可以使用共享内存来存储临时计数器，避免频繁地写入全局内存。
最后再将各 block 的结果汇总到最终的直方图中。

3. 并行归约操作

对于求和、最大值等归约操作，可以先在共享内存中执行部分归约，然后再合并结果。
这样做不仅可以减少全局内存的访问次数，还能更好地利用 GPU 的并行计算能力。

2.5 资源限制

前一小节也有提到，每一个 SM 可申请的共享内存的大小容量相对 globalMemory 小很多，每个block 可以申请的大小无法操作 SM 上资源的总量。

3.优化的方向

Global Memory 的访问模式

这里主要讨论线程访问内存地址的方式。

背景是虽然 GPU 的全局内存带宽极高，但如果访问模式不佳（随机或者分散），则实际的有效带宽可能下降一个数量级甚至更多。

本节介绍了一下几种访问模式

连续访问 128 字节，跨一个128 B段，带宽利用率 100%
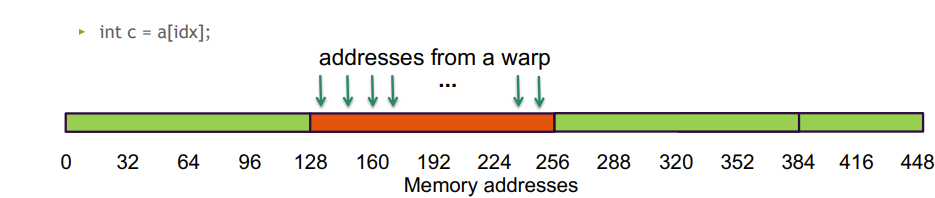
随机访问 128 字节，跨一个128 B段，和第一种一样，带宽利用率 100%
连续访问 128 字节，但跨两个128 B段，硬件需要两次内存事务来处理这 32 个int，带宽利用率 50%

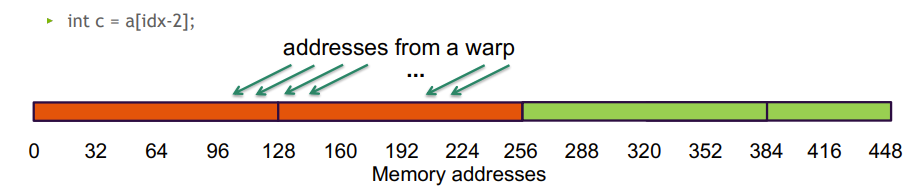
4.一个 warp 的线程访问同一个地址，带宽利用率 3.125%（1/32）。

虽然看着带宽利用率低，但代码中偶尔一次两次这样使用没什么关系，可以增加代码设计的灵活性。如果这种情况在代码中大量出现。才需要考虑如何优化。

5.一个warp 里的线程，随机跨段访问，带宽利用率 128 / (N*128) (3.125% worst case N=32)。这算是最坏的访问模式了，注意一下这种方式可能会牺牲掉一些性能。

6.在第五种访问模式的基础上，代码层面通过配置 -Xptxas -dlcm=cg 强制绕过 L1 缓存，带宽利用率 128 / (N*32) (12.5% worst case N=32)。（最坏利用率从 3.125% 提升到 12. 5%）（但视频里没有讲到代价， AI 表示这种方式谨慎使用）

启示

如果 warp 访问数据块的启示地址对齐到 128 字节的边界，更容易实现高效合并。
一个 warp 中的线程访问连续的内存区域，即所有的32 个线程访问的地址应精良落在同一个或相邻的128 字节内。避免跨多个不连续段，否则会出发多次内存事务。
使用足够多的并发访问请求，以使用满内存的总线。启动足够多的线程。
每个线程处理多个数据元素。例如一个线程连续读取4个 float 并处理，比 4个线程各读取一个更容易合并并且减少指令开销。
地址的索引计算可以复用，即避免循环中重复计算 threadIdx + blockIdx * blockDim 等。提前计算 base 地址，循环中只做增量。
充分利用所有的缓存层次。

本节的练习将展示这种差异。

Shared Memory Bank Conflicts

什么是 bank conflicts？

虽然共享内存很快，但它被划分为多个 bank（如 32 banks）。

通常有 32 个bank，每个 bank 4-byte wide。

如果 warp 中多个线程同时访问同一个 bank 的不同地址 ，就会发生 bank conflict，导致串行化访问。

共享内存的访问以 warp （32 个线程）为单位发起请求。如果在一个 warp 内的 N 个线程尝试访问同一个 bank 的不同 4字节数据，那么这些访问会被串行执行，即需要 N 次访问才可以完成原本应该并行完成的操作。典型的每个 bank 每 1 到 2 个时钟周期可以处理 4 字节数据。

但如果一个 warp 内的 N 个线程访问的是同一个bank 中的相同位置，那么这次访问只会发生一次 ，并且结果会广播给所有请求该数据的线程。甚至，如果访问的是同一个 bank 中的同一个四字节段中的不同字节，也会被视为单次访问，不会引起冲突。

如何判断是否会发生 bank conflicts？

以元素是 1 字节的数组为例， bank 的编号由字节地址对 **32 取模 ** 决定

假设共享内存数组：

复制代码

int rowSize = 32;
int colSize = 4;
__shared__ char s[rowSize * colSize];

一个 warp（32 线程）执行以下代码：

复制代码

int tid = threadIdx.x;               // 0 ~ 31
char value = s[tid * colSize + 0];         // 每个线程访问 s[0], s[4], s[8], ...,

那么一个 warp 内下标间隔 8 的线程，就会发生 bank conflict 冲突。

那么如何避免冲突？

如果是正常的连续访问

复制代码

char value = s[tid];  // 访问 s[0], s[1], s[2], ..., s[31]

就不会发生冲突。

另外如果前面给步长 colSize 加上一个 padding 1，（其实选择一个与 32 互质的数作为步长就行，又 32 为 2 的 5 次方，随便一个奇数都与 32 互质，这里加1刚好就可以）那么，这里 tid = 0 到 31，乘上步长模 32，每个 tid 对应的数将都不一样。按前面的逻辑，即 bank 不一样，即而避免冲突。

什么场景下容易遇到 bank conflict？

当我们开始利用 share memory 来进行矩阵的运算，特别是列运算的时候，比较容易遇到这个问题，本节的练习将会处理这个问题。

启示

理想模式：每个线程访问不同 bank，或同一地址（广播）。

避免方法：使用 padding（填充）打破冲突模式。

4.本节练习

4.1.了解如何使用共享内存以一维 stencil 计算为例子。

给定输入数组 u[0..N-1]，计算输出数组 v[0..N-1]，其中：

v [i ]=f (u [i −r ],u [i −r +1],...,u [i ],...,u [i +r −1],u [i +r])

r ：半径（radius）
整个 stencil 覆盖 2*r*+1 个点
f：固定的计算函数（这里 f 函数是入参求和，后续还可以推广到线性加权和等）

实现如下

复制代码

/*
 * 使用 shared memory 实现 1D stencil 计算的示例代码
 */
#include <stdio.h>
#include <algorithm>

#include "cuda_runtime.h"
#include "device_launch_parameters.h"

using namespace std;

#define N 4096
#define RADIUS 3
#define BLOCK_SIZE 16

// 期望结果是 前 RADIUS 和 后 RADIUS 个元素为 1
// 中间的 N 个元素为 1 + 2 * RADIUS
// 输入的元素是 N + 2*RADIUS 个, 输出的元素也是 N + 2*RADIUS 个
__global__ void stencil_1d(int *in, int *out)
{
    // 共享内存的大小为 BLOCK_SIZE + 2 * RADIUS
    __shared__ int temp[BLOCK_SIZE + 2 * RADIUS];
    
    // 将输入数据加载到共享内存当中, 
    // 共享内存中只有中间的 BLOCK_SIZE 个由当前 block 的线程加载的
    int gIndex = threadIdx.x + blockIdx.x * blockDim.x;
    int lindex = threadIdx.x + RADIUS;

    temp[lindex] = in[gIndex];

    // 处理边界条件, 由前 RADIUS 个线程和后 RADIUS 个线程加载
    // 这里由启动核函数时的入参来保证下面的访问不会越界
    if (threadIdx.x < RADIUS) {
        temp[lindex - RADIUS] = in[gIndex - RADIUS];
        temp[lindex + BLOCK_SIZE] = in[gIndex + BLOCK_SIZE];
    }

    // 同步线程，确保数据加载完成
    __syncthreads();

    // 应用 stencil 计算
    int result = 0;
    for (int offset = -RADIUS; offset <= RADIUS; offset++) {
        result += temp[lindex + offset];
    }

    // 将结果存储回全局内存
    out[gIndex] = result;
}

int main(void)
{
    int *in, *out;
    int *d_in, *d_out; // device copies of a, b, c
    int size = (N + 2*RADIUS) * sizeof(int);

    // 分配主机侧内存并初始化数据, 全都以 1 赋值
    in = (int *)malloc(size); 
    fill_n(in, N + 2*RADIUS, 1);
    out = (int *)malloc(size); 
    fill_n(out, N + 2*RADIUS, 1);

    // 分配设备侧内存
    cudaMalloc((void**)&d_in, size);
    cudaMalloc((void**)&d_out, size);

    // 将数据从主机复制到设备
    cudaMemcpy(d_in, in, size, cudaMemcpyHostToDevice);
    cudaMemcpy(d_out, out, size, cudaMemcpyHostToDevice);

    // 启动 stencil_1d kernel
    stencil_1d<<<N/BLOCK_SIZE,BLOCK_SIZE>>>(d_in + RADIUS, d_out + RADIUS);
    

    // 将结果从设备复制回主机
    cudaMemcpy(out, d_out, size, cudaMemcpyDeviceToHost);

    // Error Checking
    for (int i = 0; i < N + 2*RADIUS; i++) {
        if (i<RADIUS || i>=N+RADIUS){
        if (out[i] != 1)
            printf("Mismatch at index %d, was: %d, should be: %d\n", i, out[i], 1);
        } else {
        if (out[i] != 1 + 2*RADIUS)
            printf("Mismatch at index %d, was: %d, should be: %d\n", i, out[i], 1 + 2*RADIUS);
        }
    }

    // Cleanup
    free(in); 
    free(out);
    cudaFree(d_in); 
    cudaFree(d_out);
    printf("Success!\n");
    return 0;
}

4.2 使用共享内存实现 tiled based 方法矩阵乘法

问题背景：朴素矩阵乘法的问题

计算 C =A ×B，其中：

A 是 M ×K
B 是 K ×N
C 是 M ×N

朴素 CUDA 实现（每个线程算一个 C[i][j]）：

复制代码

C[i][j] = 0;
for (int k = 0; k < K; ++k)
    C[i][j] += A[i][k] * B[k][j];

问题：

大量重复读取：A 中的第 i 行所有数据，要与 B 的每一列做乘法时，都会被读取一遍，会被重复读取 N 遍。同样的 B 的第 j 列会与 A 的每一行做乘法，会被重复读取 M 遍。

大量的 global Memory 访问： 每次乘加都访问 DRAM，效率较低，没有充分运用多层次的内存结构

实现思路：

Tiled 方法的核心思想: 把 A 和 B 都划分为小块（tile）。把 A 的 tile 与 B 的tile 先加载到 shared memory，然后反复使用，减少全局内存的访问。

设定 tile 大小： TILE_SIZE = 16 或 32（通常 ≤ 32，受限于 shared memory 和 bank conflict）。

每个 block 负责计算 C 中一个 TILE_SIZE × TILE_SIZE 的子块。

每个线程负责计算该子块中的 一个或多个元素。

全局内存访问次数从 O(M×N×K) 降至 O((M×N×K)/TILE_SIZE)。

本次练习就先实现 N * N 的矩阵乘法。

复制代码

/*
* 使用 shared mamory 实现基于 tied based 的矩阵乘法
*/

#include <stdio.h>
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <algorithm>

#include <time.h>  // 用于统计运行时间


// error checking macro
#define cudaCheckErrors(msg)                             \
  do                                                     \
  {                                                      \
    cudaError_t __err = cudaGetLastError();              \
    if (__err != cudaSuccess)                            \
    {                                                    \
      fprintf(stderr, "Fatal error: %s (%s at %s:%d)\n", \
              msg, cudaGetErrorString(__err),            \
              __FILE__, __LINE__);                       \
      fprintf(stderr, "*** FAILED - ABORTING\n");        \
      exit(1);                                           \
    }                                                    \
  } while (0)


const int DSIZE = 8192;
const int BLOCK_SIZE = 32;  // CUDA maximum is 1024 *total* threads in block
const float A_VALUE = 3.0f;
const float B_VALUE = 2.0f;

__global__ void tiled_based_matrix_multiply(const float *matrixA, const float *matrixB, float *matrixC, int ds) {
    // 每个 block 申请 BLOCK_SIZE * BLOCK_SIZE 大小的共享内存
    __shared__ float tileA[BLOCK_SIZE][BLOCK_SIZE];
    __shared__ float tileB[BLOCK_SIZE][BLOCK_SIZE];
    // 获取 block 中二维排布的线程 id
    int idx = threadIdx.x + blockDim.x * blockIdx.x;
    int idy = threadIdx.y + blockDim.y * blockIdx.y;
    
    // 判断 线程 id 访问矩阵是否会超出边界
    if ((idx < ds) && (idy < ds)) {
        float cIdyIdx = 0;
        // 启循环 将 A tile 与 B tile 的数据从 globalMemory 加载到共享内存当中（注意数据同步）
        for (int i = 0; i < ds / BLOCK_SIZE; i++) {
            // 注意 tile[][] 矩阵里是先跟行号再跟列号， 所以y 在前 x 在后
            // tileA 按照行的方向一个一个获取， tileB 则按照列的方向 一个一个获取。
            // 访问 输入矩阵的时候使用 ds * rowId， 表示取到第 row 行 
            // tileA 的行号与 idy 相同， 列号为 (i * blockDim.x + threadIdx.x)
            // tileB 的行号为(i * blockDim.y + threadIdx.y), 列号与 idx 相同，
            tileA[threadIdx.y][threadIdx.x] = matrixA[ds * idy + (i * blockDim.x + threadIdx.x)];
            tileB[threadIdx.y][threadIdx.x] = matrixB[ds * (i * blockDim.y + threadIdx.y) + idx];
        
            // Synchronize
            __syncthreads();

            // 加载 完 tile 数据之后，在循环中启动循环， 将tile 的计算结果进行求和 
            for (int k = 0; k < BLOCK_SIZE; k++) {
                cIdyIdx += tileA[threadIdx.y][k] * tileB[k][threadIdx.x];
            }
            __syncthreads();
        }

        // 将计算结果 写回 C 当中
        matrixC[idy * ds + idx] = cIdyIdx;
    }
}

void matrix_multiply_CPU(const float *matrixA, const float *matrixB, float *matrixC, int ds) {
    // 三重循环计算 C = A * B
    for (int i = 0; i < ds; ++i) {          // C 的行
        for (int j = 0; j < ds; ++j) {      // C 的列
            float sum = 0.0f;
            for (int k = 0; k < ds; ++k) {  // 点积维度
                sum += matrixA[i * ds + k] * matrixB[k * ds + j];
            }
            matrixC[i * ds + j] = sum;
        }
    }
}


int main() {
    float* h_A, * h_B, * h_C, * d_A, * d_B, * d_C;

    // these are just for timing
    clock_t t0, t1, t2;
    double t1sum = 0.0;
    double t2sum = 0.0;

    // start timing
    t0 = clock();

    h_A = new float[DSIZE * DSIZE];
    h_B = new float[DSIZE * DSIZE];
    h_C = new float[DSIZE * DSIZE];

    for (int i = 0; i < DSIZE * DSIZE; i++) {
        h_A[i] = A_VALUE;
        h_B[i] = B_VALUE;
        h_C[i] = 0;
    }

    // Initialization timing
    t1 = clock();
    t1sum = ((double)(t1 - t0)) / CLOCKS_PER_SEC;
    printf("Init took %f seconds.  Begin compute\n", t1sum);

    // Allocate device memory and copy input data over to GPU
    cudaMalloc(&d_A, DSIZE * DSIZE * sizeof(float));
    cudaMalloc(&d_B, DSIZE * DSIZE * sizeof(float));
    cudaMalloc(&d_C, DSIZE * DSIZE * sizeof(float));
    cudaCheckErrors("cudaMalloc failure");
    cudaMemcpy(d_A, h_A, DSIZE * DSIZE * sizeof(float), cudaMemcpyHostToDevice);
    cudaMemcpy(d_B, h_B, DSIZE * DSIZE * sizeof(float), cudaMemcpyHostToDevice);
    cudaCheckErrors("cudaMemcpy H2D failure");

    // Launch kernel
    // 这一次将 block 以二维的形式来排布
    dim3 block(BLOCK_SIZE, BLOCK_SIZE);
    dim3 grid((DSIZE + block.x - 1) / block.x, (DSIZE + block.y - 1) / block.y);
    tiled_based_matrix_multiply<<<grid, block>>>(d_A, d_B, d_C, DSIZE);
    cudaCheckErrors("kernel launch failure");

    cudaMemcpy(h_C, d_C, DSIZE * DSIZE * sizeof(float), cudaMemcpyDeviceToHost);

    // GPU timing
    t2 = clock();
    t2sum = ((double)(t2 - t1)) / CLOCKS_PER_SEC;
    printf("tiled_based_matrix_multiply Done. Compute took %f seconds\n", t2sum);


    // Verify results
    cudaCheckErrors("kernel execution failure or cudaMemcpy H2D failure");
    for (int i = 0; i < DSIZE * DSIZE; i++) {
        if (h_C[i] != A_VALUE * B_VALUE * DSIZE) { 
            printf("mismatch at index %d, was: %f, should be: %f\n", i, h_C[i], A_VALUE * B_VALUE * DSIZE); 
            return -1; 
        }
    }
        
    printf("Success!\n");

    // 下面这个就只是试试，两三分钟没跑完就撤了
    //t1 = clock();
    //matrix_multiply_CPU(h_A, h_B, h_C, DSIZE);
    //t2 = clock();
    //t2sum = ((double)(t2 - t1)) / CLOCKS_PER_SEC;
    //printf("matrix_multiply_CPU Compute Done. took %f seconds\n", t2sum);

    //for (int i = 0; i < DSIZE * DSIZE; i++) {
    //    if (h_C[i] != A_VALUE * B_VALUE * DSIZE) { 
    //        printf("mismatch at index %d, was: %f, should be: %f\n", i, h_C[i], A_VALUE * B_VALUE * DSIZE); 
    //        return -1; 
    //    }
    //}

    // free device memory
    cudaFree(d_A);
    cudaFree(d_B);
    cudaFree(d_C);

    // free host memory
    delete[] h_A;
    delete[] h_B;
    delete[] h_C;
    return 0;
}

4.3 通过矩阵的行列加法，验证连续访问与不连续访问的影响

复制代码

/*
 * grid stride 方法实现向量加法
 */
#include <stdio.h>
#include <stdlib.h>

#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <algorithm>

#include <chrono>

// error checking macro
#define cudaCheckErrors(msg)                             \
  do                                                     \
  {                                                      \
    cudaError_t __err = cudaGetLastError();              \
    if (__err != cudaSuccess)                            \
    {                                                    \
      fprintf(stderr, "Fatal error: %s (%s at %s:%d)\n", \
              msg, cudaGetErrorString(__err),            \
              __FILE__, __LINE__);                       \
      fprintf(stderr, "*** FAILED - ABORTING\n");        \
      exit(1);                                           \
    }                                                    \
  } while (0)

const size_t DSIZE = 16384; // matrix side dimension
const int block_size = 256; // CUDA maximum is 1024

// matrix row-sum kernel
__global__ void row_sums(const float *A, float *sums, size_t ds)
{

  int idx = threadIdx.x + blockDim.x * blockIdx.x; // create typical 1D thread index from built-in variables
  if (idx < ds)
  {
    float sum = 0.0f;
    for (size_t i = 0; i < ds; i++)
    {
      sum += A[idx * ds + i]; // write a for loop that will cause the thread to iterate across a row, keeeping a running sum, and write the result to sums
    }
    sums[idx] = sum;
  }
}

// matrix column-sum kernel
__global__ void column_sums(const float *A, float *sums, size_t ds)
{

  int idx = threadIdx.x + blockDim.x * blockIdx.x; // create typical 1D thread index from built-in variables
  if (idx < ds)
  {
    float sum = 0.0f;
    for (size_t i = 0; i < ds; i++)
    {
      sum += A[i * ds + idx]; // write a for loop that will cause the thread to iterate down a column, keeeping a running sum, and write the result to sums
    }
    sums[idx] = sum;
  }
}

bool validate(float *data, size_t sz)
{
  for (size_t i = 0; i < sz; i++)
    if (data[i] != (float)sz)
    {
      printf("results mismatch at %lu, was: %f, should be: %f\n", i, data[i], (float)sz);
      return false;
    }
  return true;
}

int main()
{

  float *h_A, *h_sums, *d_A, *d_sums;
  h_A = new float[DSIZE * DSIZE]; // allocate space for data in host memory
  h_sums = new float[DSIZE]();

  for (int i = 0; i < DSIZE * DSIZE; i++) // initialize matrix in host memory
    h_A[i] = 1.0f;

  cudaMalloc(&d_A, DSIZE * DSIZE * sizeof(float)); // allocate device space for A
  cudaMalloc(&d_sums, DSIZE * sizeof(float));      // allocate device space for vector d_sums
  cudaCheckErrors("cudaMalloc failure");           // error checking

  // copy matrix A to device:
  cudaMemcpy(d_A, h_A, DSIZE * DSIZE * sizeof(float), cudaMemcpyHostToDevice);
  cudaCheckErrors("cudaMemcpy H2D failure");

  // cuda processing sequence step 1 is complete
  auto t0 = std::chrono::high_resolution_clock::now();
  row_sums<<<(DSIZE + block_size - 1) / block_size, block_size>>>(d_A, d_sums, DSIZE);
  cudaDeviceSynchronize();

  auto t1 = std::chrono::high_resolution_clock::now();
  auto ms = std::chrono::duration_cast<std::chrono::milliseconds>(t1 - t0).count();
  printf("row_sums: elapsed: %lld ms\n", static_cast<long long>(ms));

  cudaCheckErrors("kernel launch failure");
  // cuda processing sequence step 2 is complete

  // copy vector sums from device to host:
  cudaMemcpy(h_sums, d_sums, DSIZE * sizeof(float), cudaMemcpyDeviceToHost);

  // cuda processing sequence step 3 is complete
  cudaCheckErrors("kernel execution failure or cudaMemcpy H2D failure");

  if (!validate(h_sums, DSIZE))
    return -1;
  printf("row sums correct!\n");

  cudaMemset(d_sums, 0, DSIZE * sizeof(float));

  t0 = std::chrono::high_resolution_clock::now();
  column_sums<<<(DSIZE + block_size - 1) / block_size, block_size>>>(d_A, d_sums, DSIZE);
  cudaDeviceSynchronize();

  t1 = std::chrono::high_resolution_clock::now();
  ms = std::chrono::duration_cast<std::chrono::milliseconds>(t1 - t0).count();
  printf("column_sums: elapsed: %lld ms\n", static_cast<long long>(ms));

  cudaCheckErrors("kernel launch failure");
  // cuda processing sequence step 2 is complete

  // copy vector sums from device to host:
  cudaMemcpy(h_sums, d_sums, DSIZE * sizeof(float), cudaMemcpyDeviceToHost);
  // cuda processing sequence step 3 is complete
  cudaCheckErrors("kernel execution failure or cudaMemcpy H2D failure");

  if (!validate(h_sums, DSIZE))
    return -1;
  printf("column sums correct!\n");
  return 0;
}

执行结果如下

复制代码

row_sums: elapsed: 64 ms
row sums correct!
column_sums: elapsed: 22 ms
column sums correct!

列和更快, 列和一个 warp 里不同的线程，可以访问连续相邻的内存，行和则会存在跨段的现象。

Analysis-Driven Optimization: http://on-demand.gputechconf.com/gtc/2012/presentations/S0514-GTC2012-GPU-PerformanceAnalysis.pdf

CUDA Best Practices Guide: https://docs.nvidia.com/cuda/cuda-c-best-practices-guide/index.html

CUDA Tuning Guides: https://docs.nvidia.com/cuda/index.html#programming-guides

【CUDA笔记】03 CUDA GPU 架构与一般的程序优化思路（下）

引言

1.GPU 的内存结构

Local storage

Shared memory / L1

L2

GLobalMemory

2.Shared Memory

2.1 什么是共享内存， 这一设计起到什么作用？

2.2 共享内存如何使用

2.3 同步机制

2.4 应用场景

1. 矩阵乘法

2. 直方图计算

3. 并行归约操作

2.5 资源限制

3.优化的方向

Global Memory 的访问模式

启示

Shared Memory Bank Conflicts

什么是 bank conflicts？

如何判断是否会发生 bank conflicts？

什么场景下容易遇到 bank conflict？

启示

4.本节练习

4.1.了解如何使用共享内存 以 一维 stencil 计算为例子。

4.2 使用共享内存实现 tiled based 方法矩阵乘法

4.3 通过矩阵的行列加法， 验证连续访问与不连续访问的影响

本节推荐读物

2.1 什么是共享内存，这一设计起到什么作用？

4.1.了解如何使用共享内存以一维 stencil 计算为例子。

4.3 通过矩阵的行列加法，验证连续访问与不连续访问的影响