引言:
这是最近接触的一个新算法,历时多天终于明白其中的道理,我在这里分享一点个人的感悟,希望对大家有所帮助。
背景:
问题起源
发明者:法国数学家爱德华·卢卡斯(Édouard Lucas)于1883年发明
传说背景:源于一个古老的印度传说,描述在贝拿勒斯(现瓦拉纳西)的寺庙中有三根钻石柱子,上帝创造世界时在第一根柱子上放置了64个金盘,要求僧侣将所有盘子移到第三根柱子上
问题规则
三根柱子:通常标记为 A(起始柱)、B(辅助柱)、C(目标柱)
盘子特性:有 n 个不同大小的盘子,大盘不能放在小盘上面
移动限制:每次只能移动一个盘子,且只能移动到相邻的柱子上
目标:将所有盘子从起始柱 A 移动到目标柱 C
数学模型
汉诺塔属于典型的递归问题,但是递归问题又是什么呢?
递归定义
递归是一种编程技术,指函数直接或间接地调用自身来解决问题的方法。
(个人理解就是不断向前推,直到推到能用具体情况计算位置)不保证理解正确
递归的核心要素
基础情况(Base Case):递归的终止条件,防止无限循环
递归情况(Recursive Case):函数调用自身的部分,通常处理规模更小的子问题
递归的特点
自我调用:函数在执行过程中会调用自身
问题分解:将复杂问题分解为相同类型的更小子问题
规模缩减:每次递归调用都使问题规模变小
栈结构:系统使用调用栈来管理递归过程中的函数调用
递归的应用场景
数学计算:阶乘、斐波那契数列等
数据结构遍历:树、图的深度优先搜索
分治算法:快速排序、归并排序
经典问题:汉诺塔、八皇后等
正文:
大多数人的困惑其实是不理解其内部的移动逻辑,从而无法看懂抽象的函数。所以我以4层汉诺塔为例,详细解释它的运行规律。
目的:将A柱上的四层盘子移到C柱。
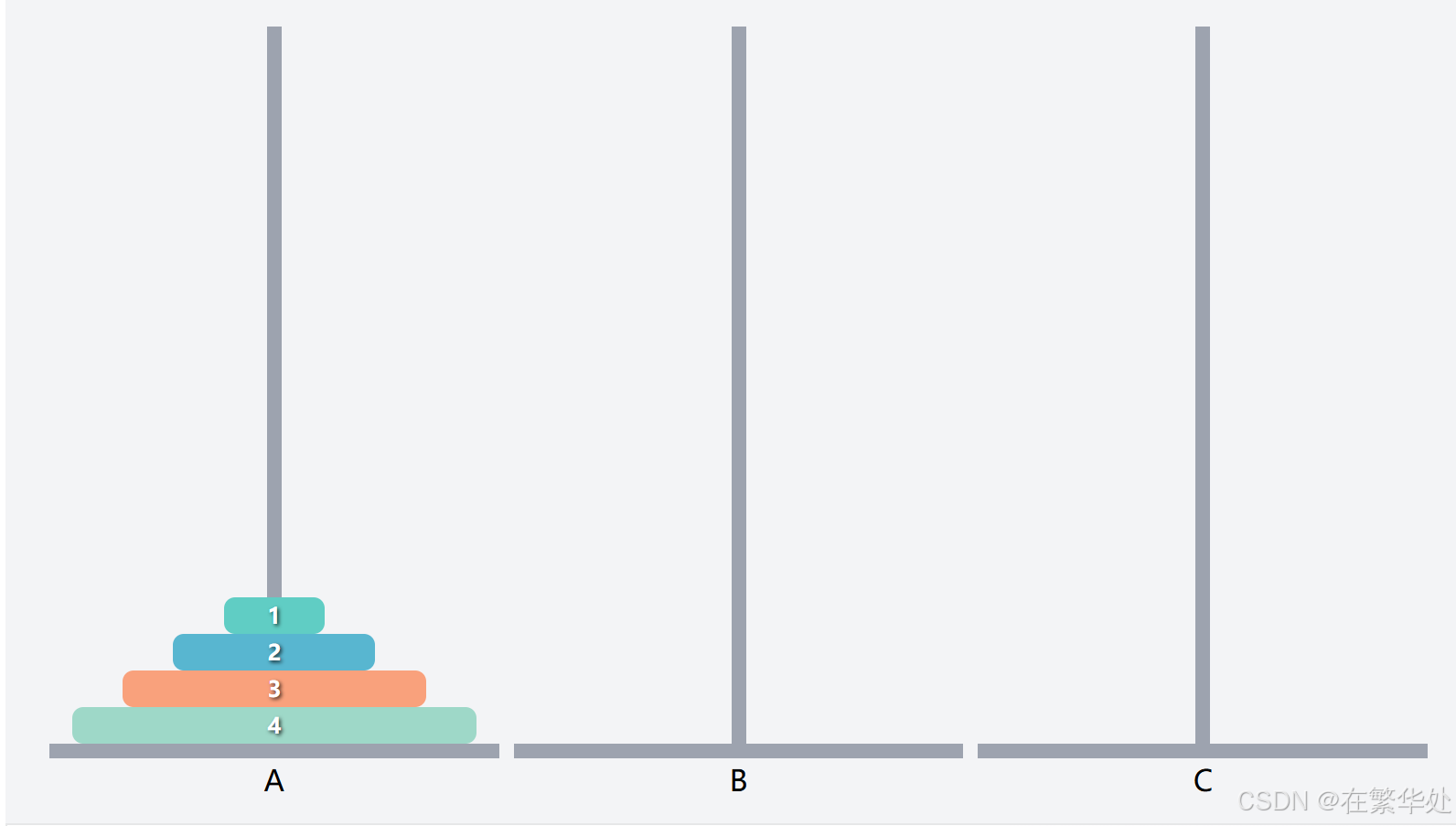
因为汉诺塔上小下大放置的规则,下图是此算法的灵魂所在。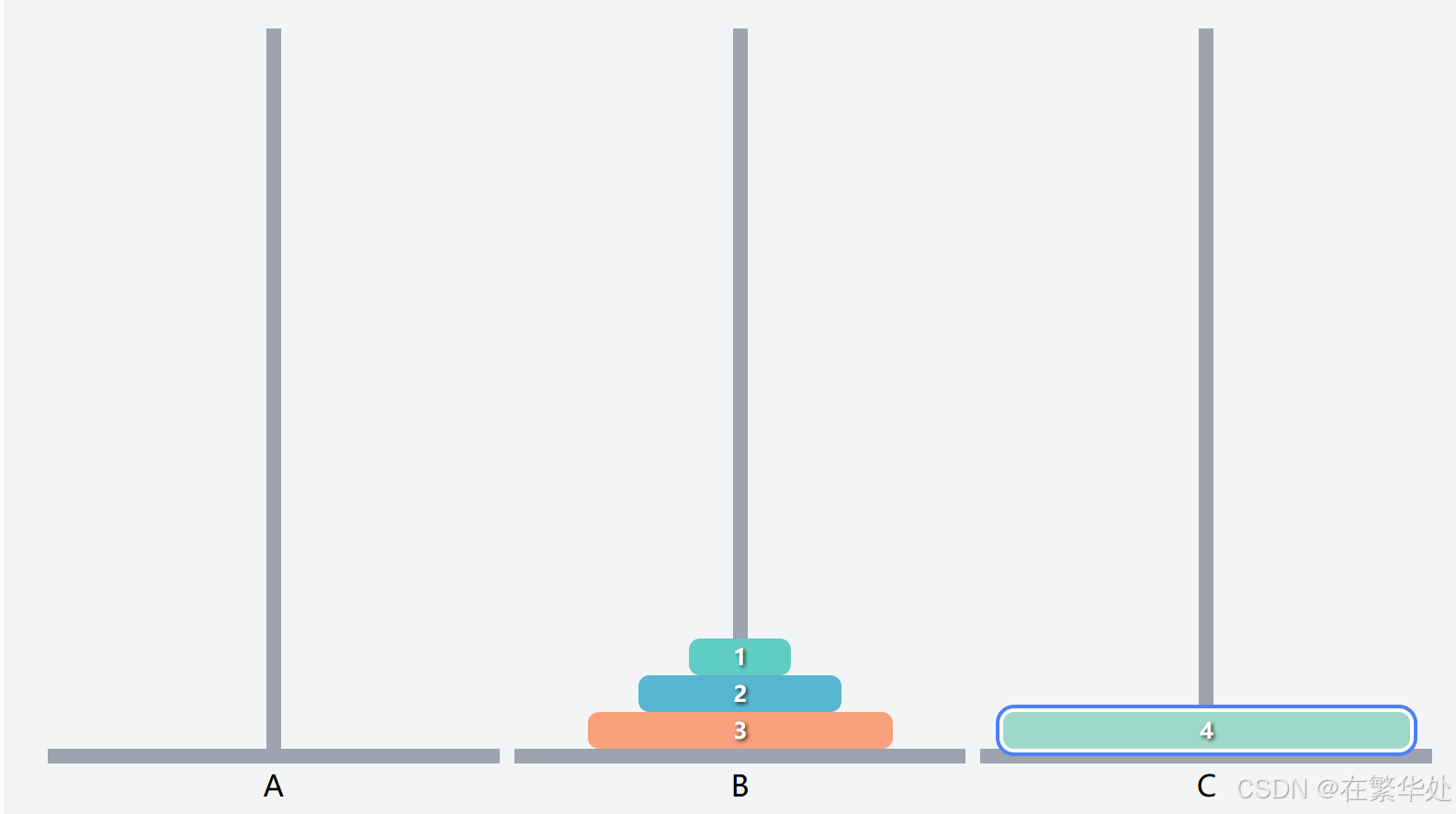
为什么这是灵魂所在呢?其实这就牵扯到递归的思想了。
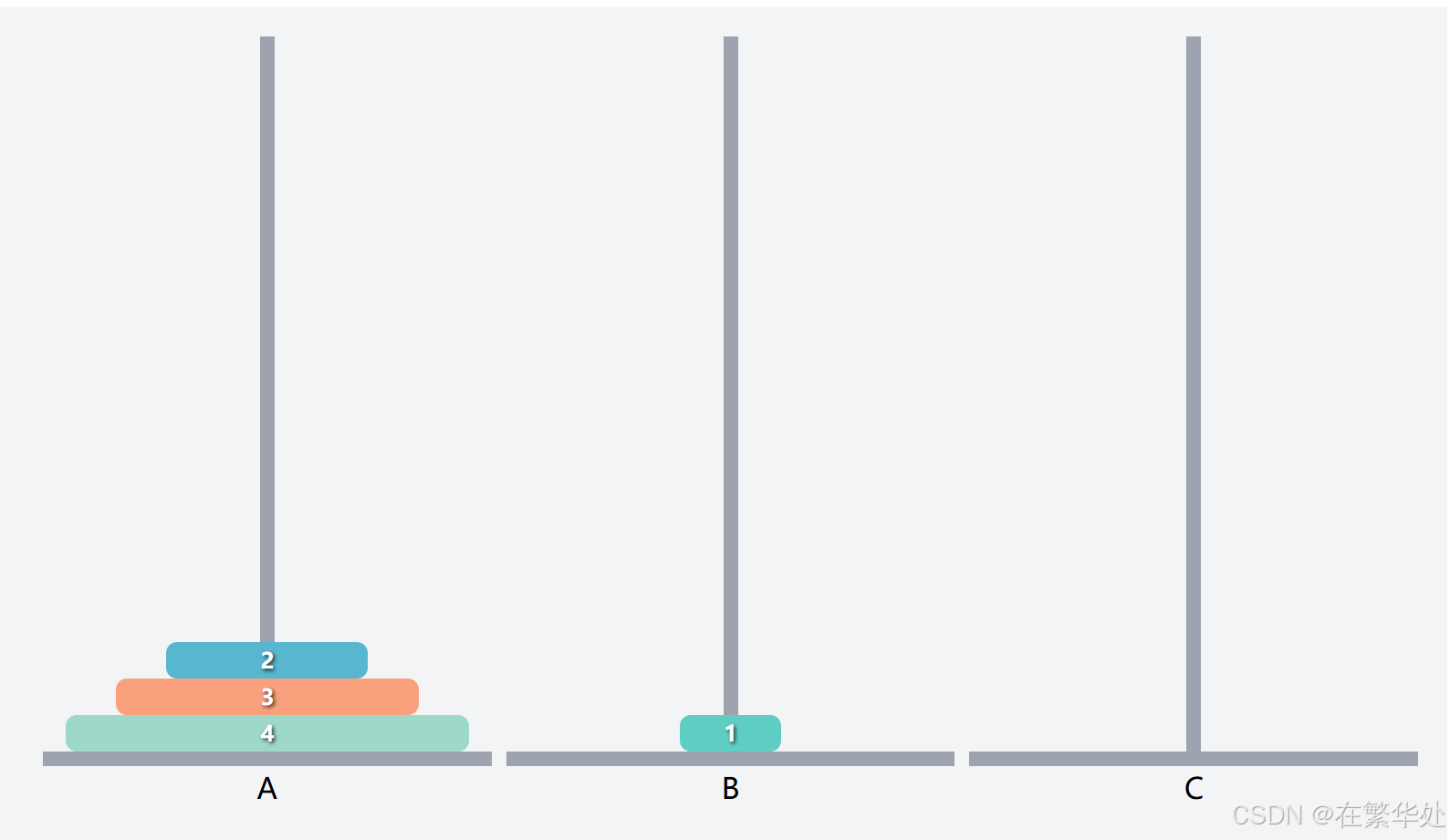
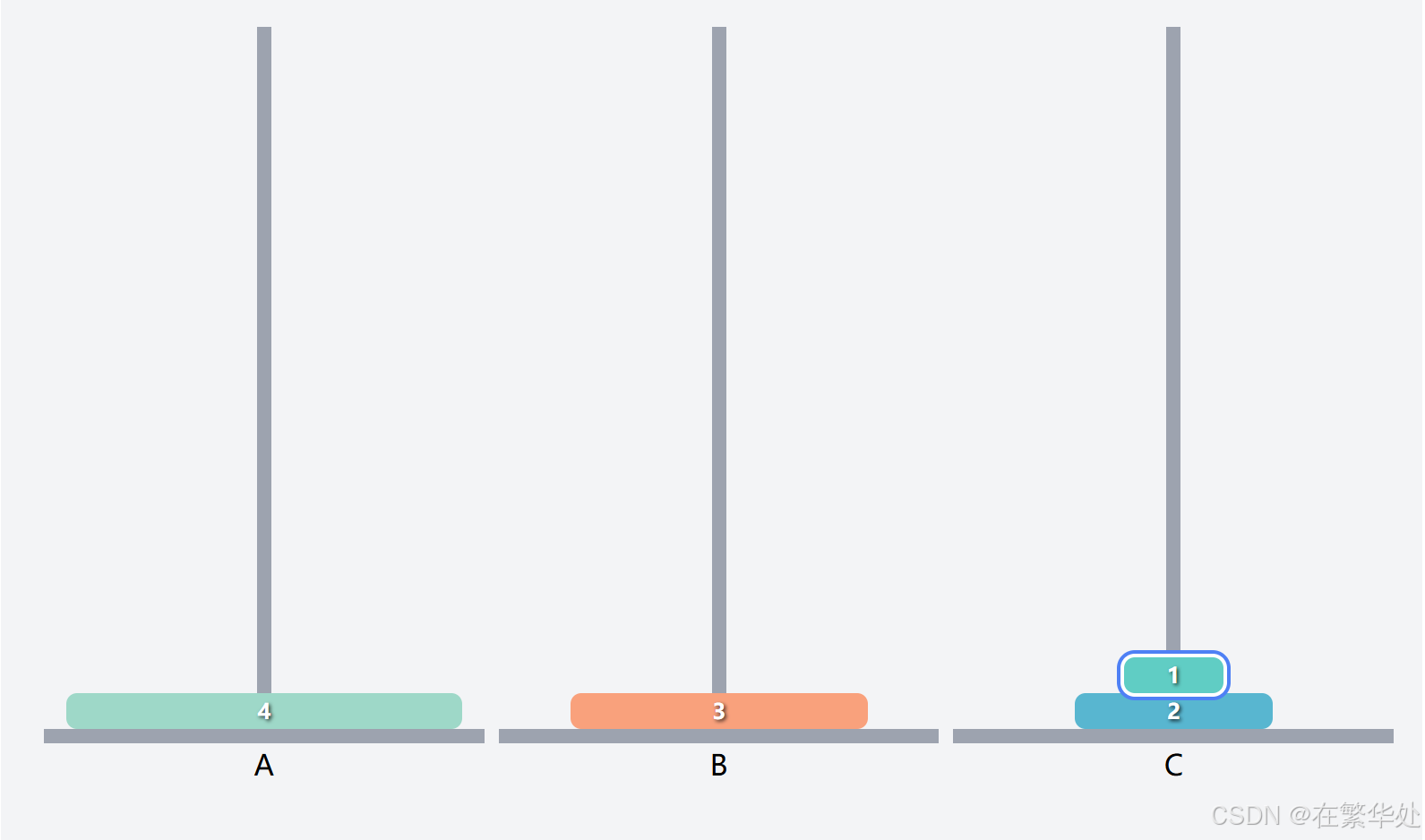
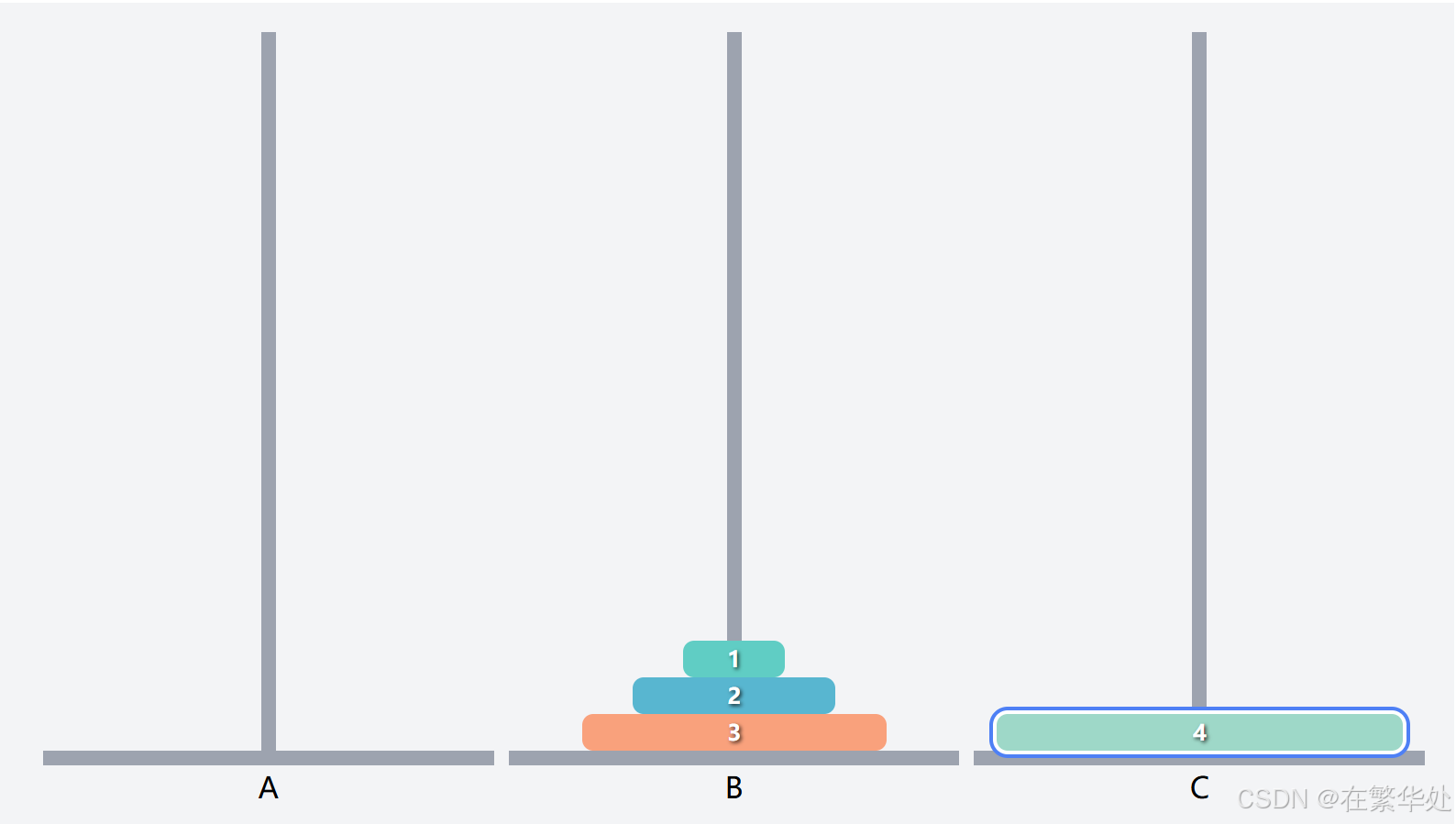
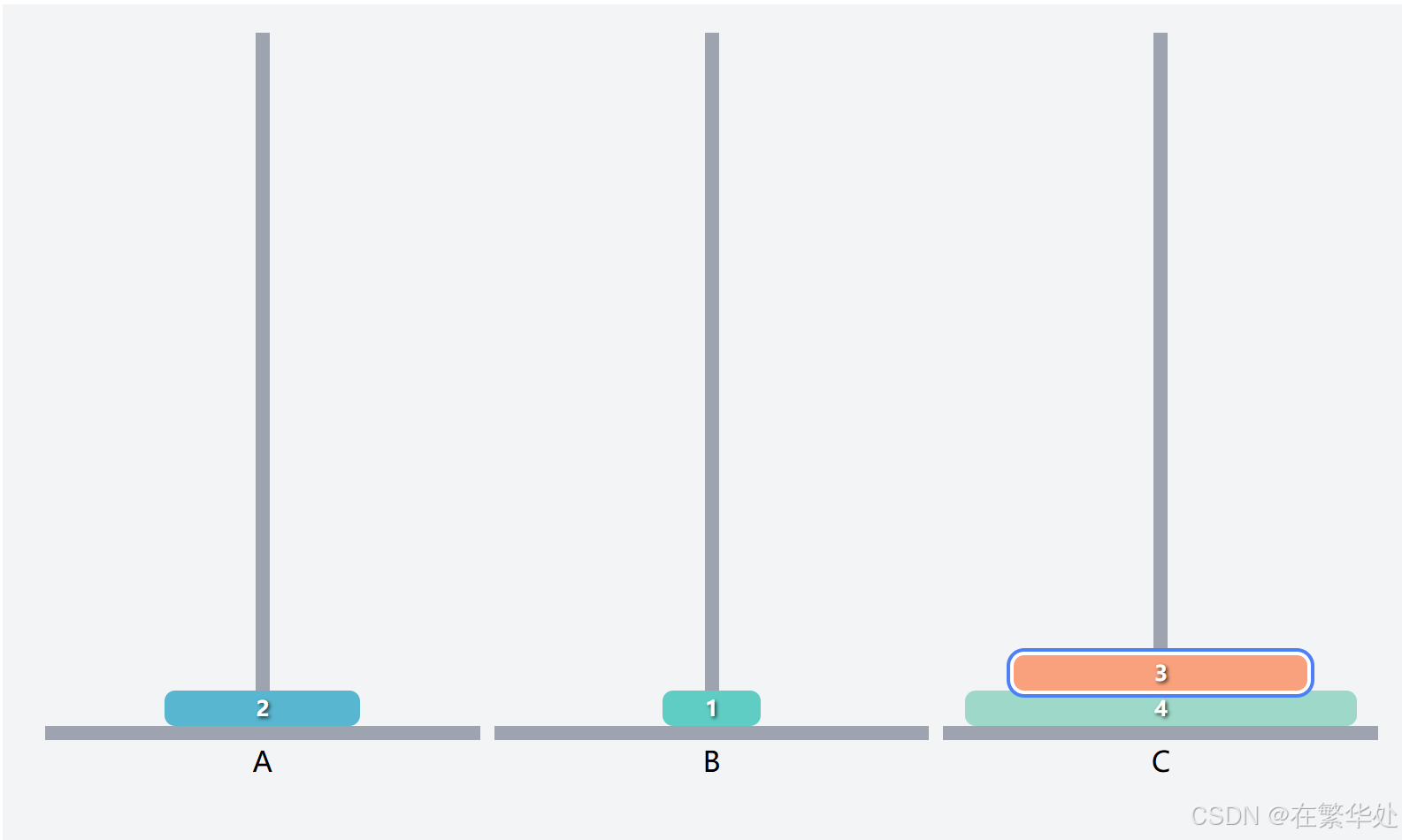
我们不妨先假设上3层为一个整体Q,要想把序号4的盘子移到目标柱C,需要先把Q移到辅助柱B,再将序号4的盘子移动到目标柱C。(此步即将问题简化为两层,也是递归最终的位置)
而接下来我们需将Q从起始柱B移动到目标柱C。(完成最终的移动)
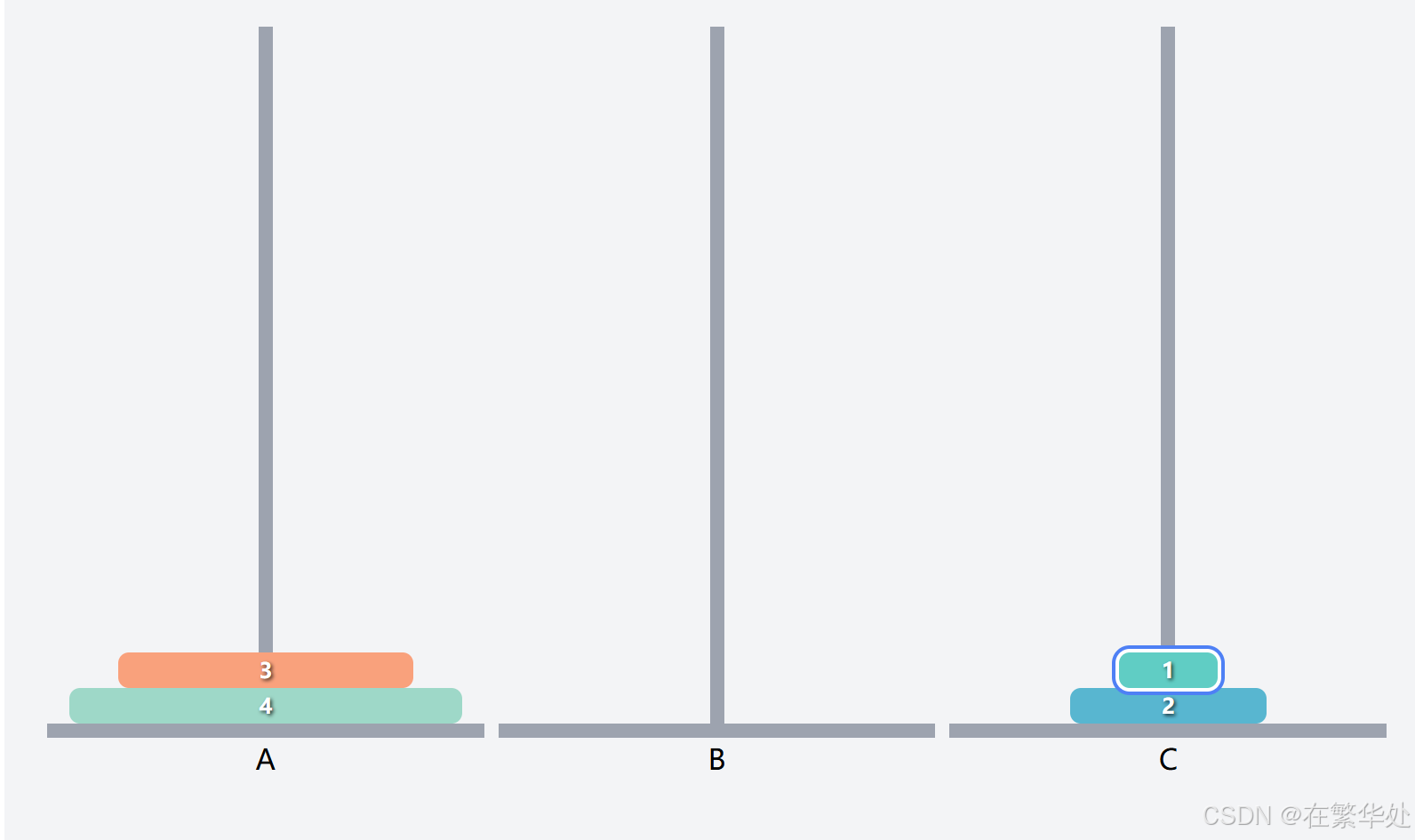
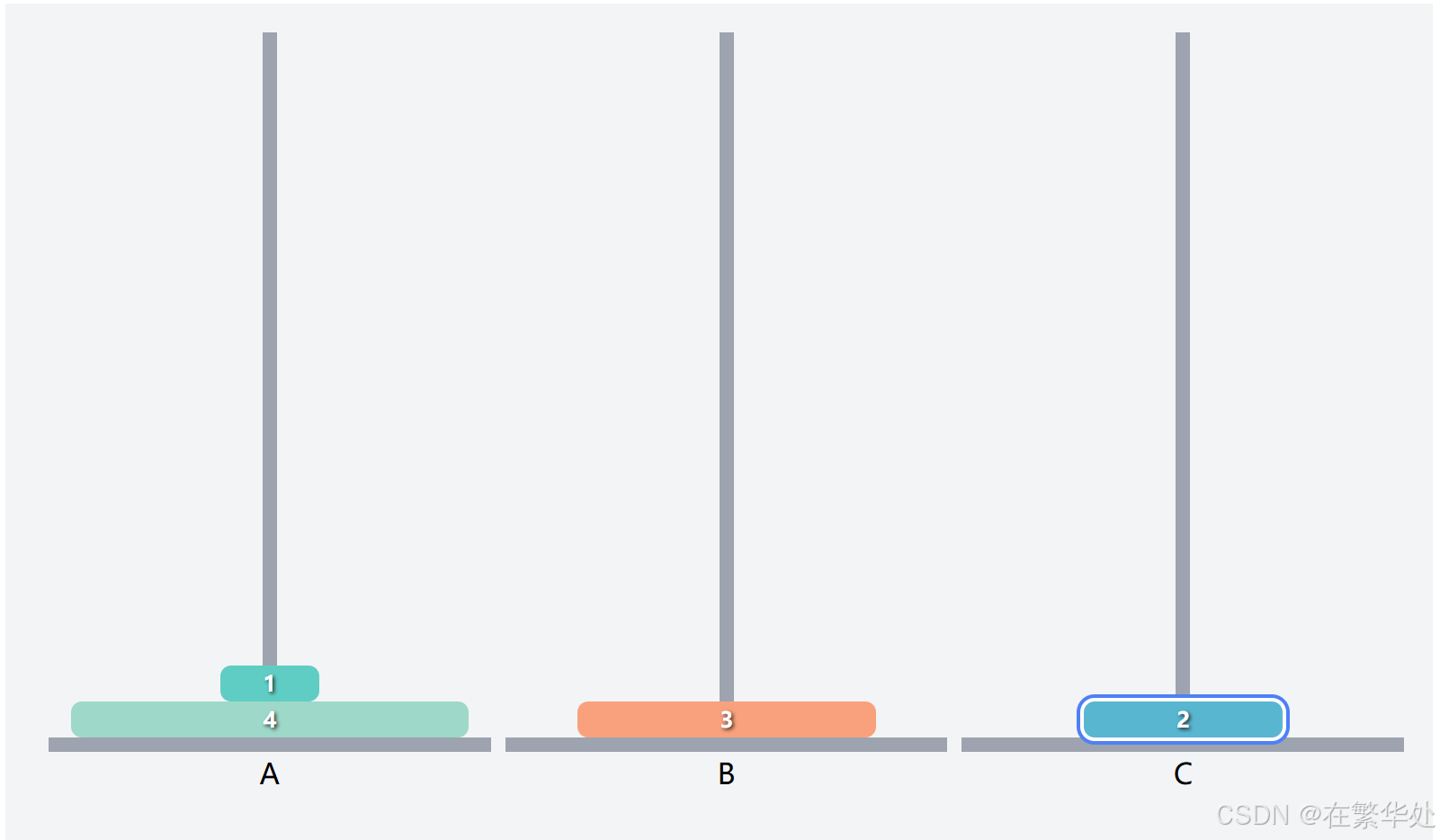
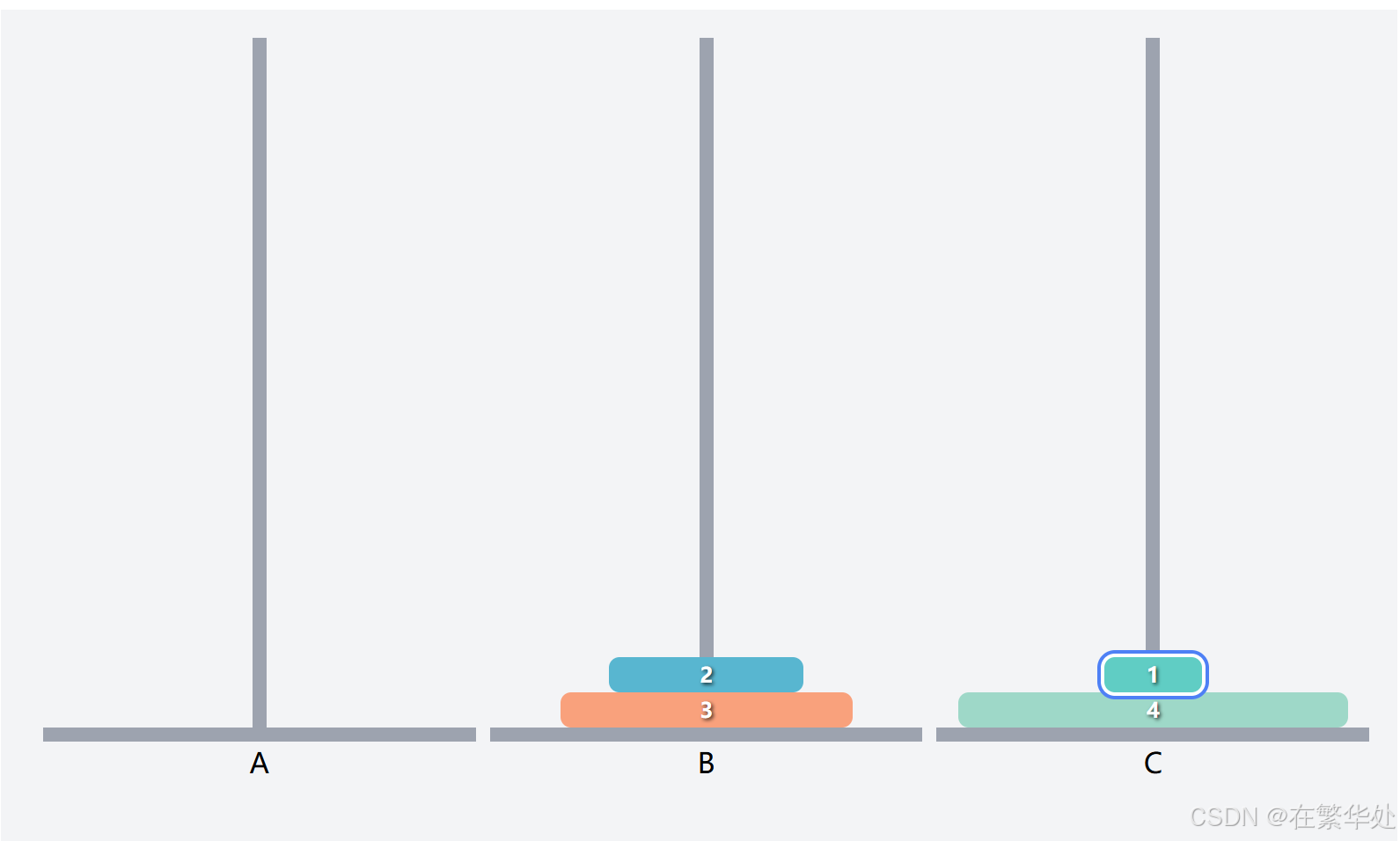
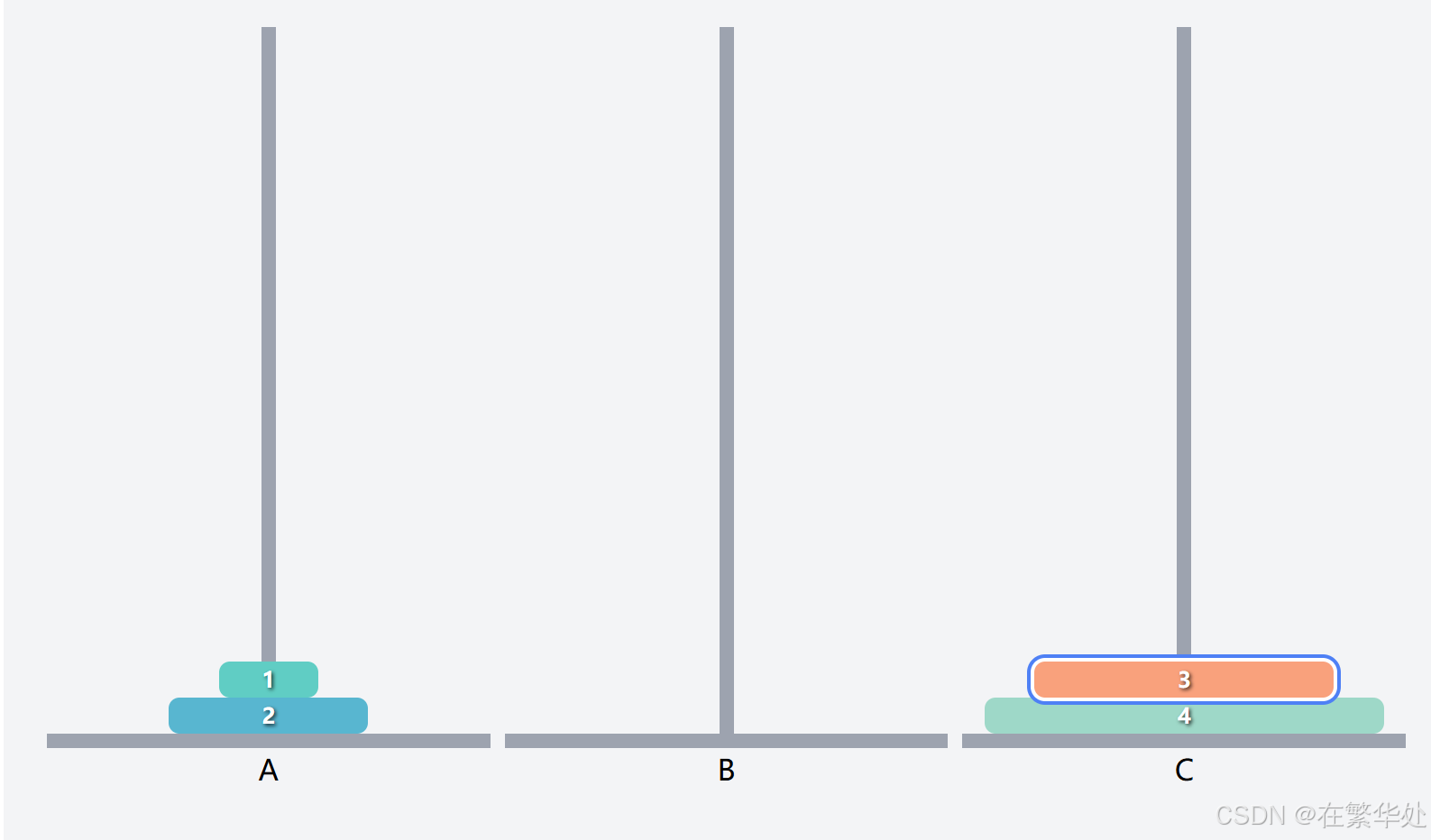
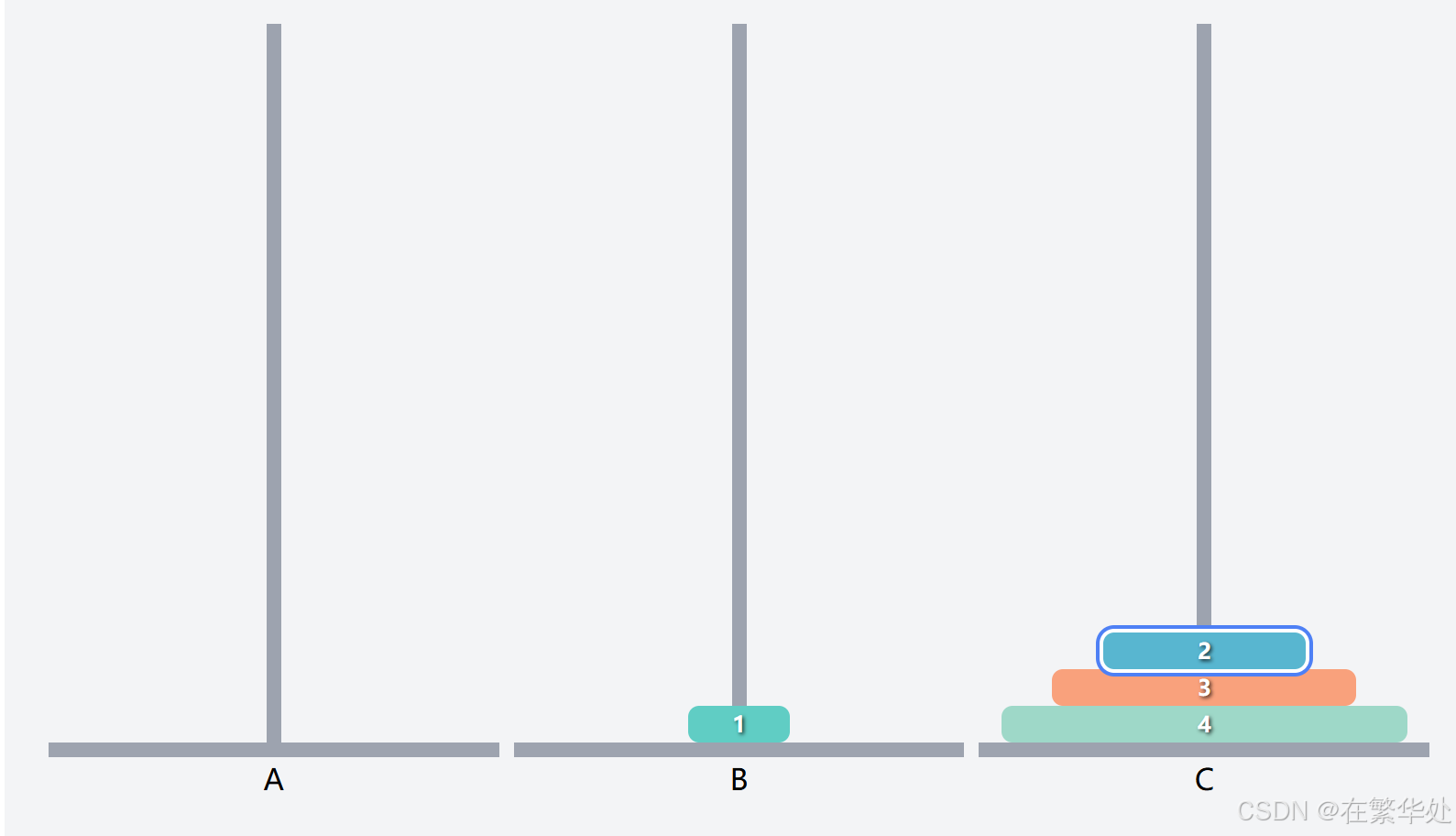
这就是一个新的汉诺塔问题了,假设上两层为一个整体Q2,要想把序号3的盘子起始柱B移到目标柱C,需要先把Q移辅助柱A,再将序号3的盘子移动到目标柱C。(注意起始柱、辅助柱、目标柱的调换)
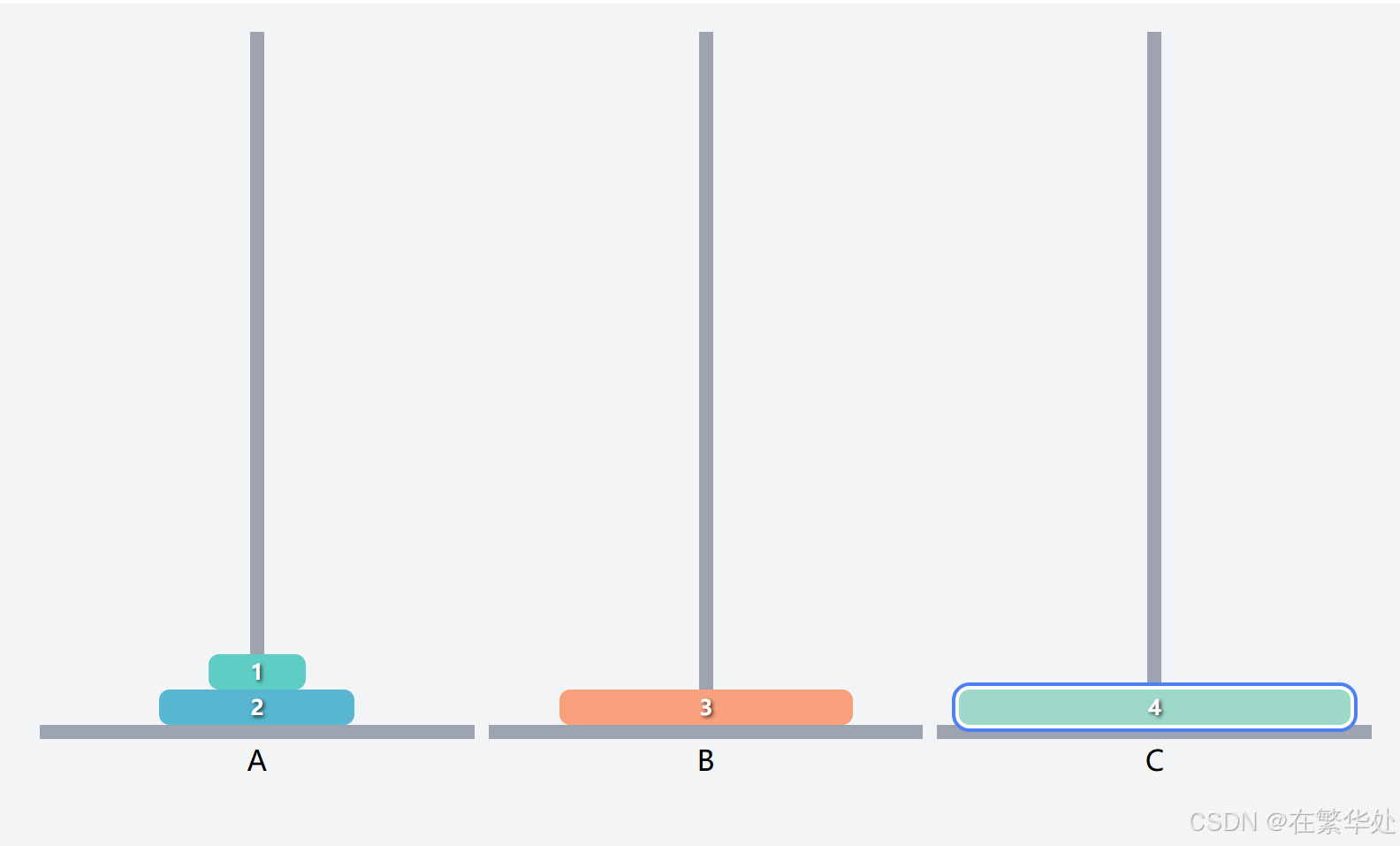
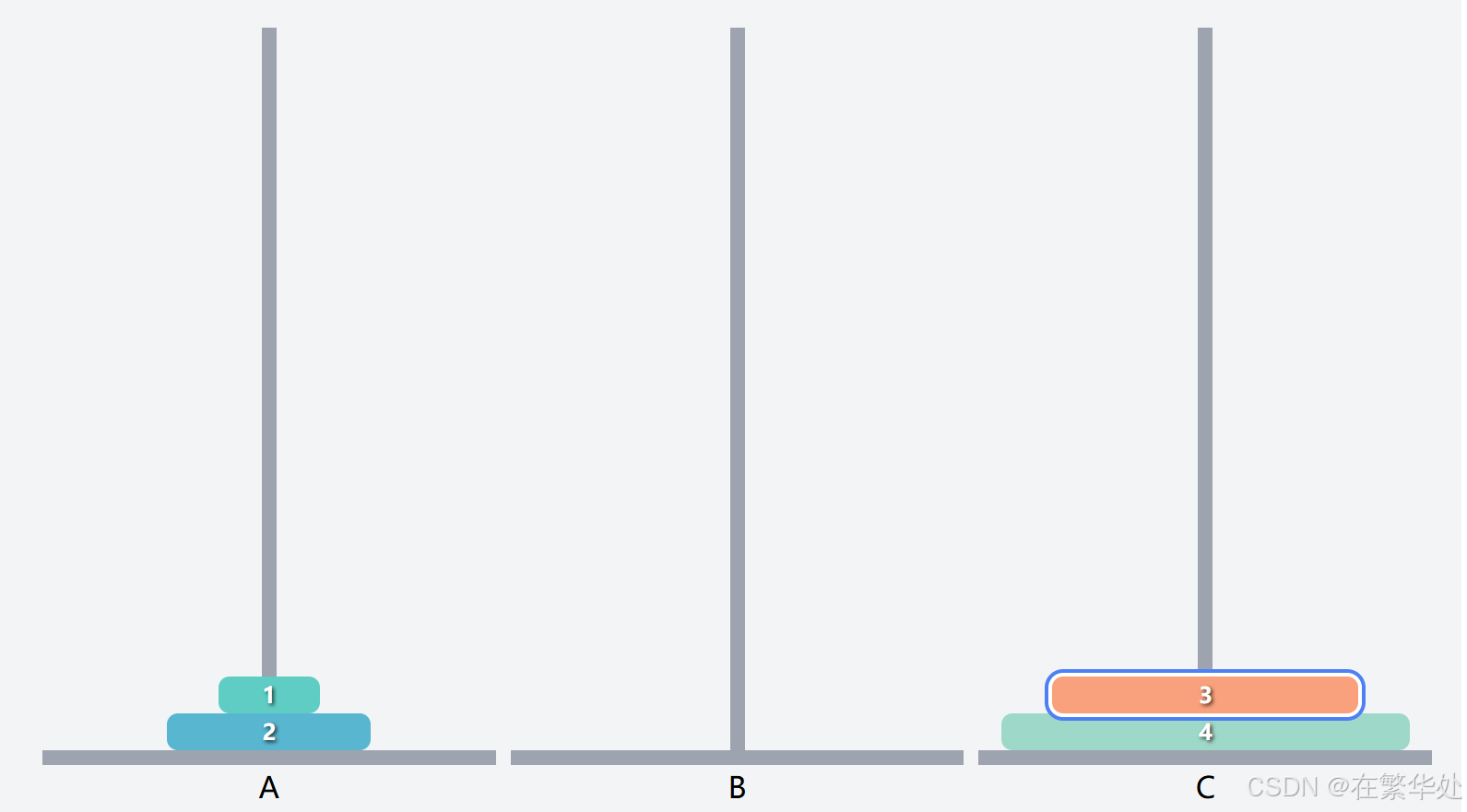
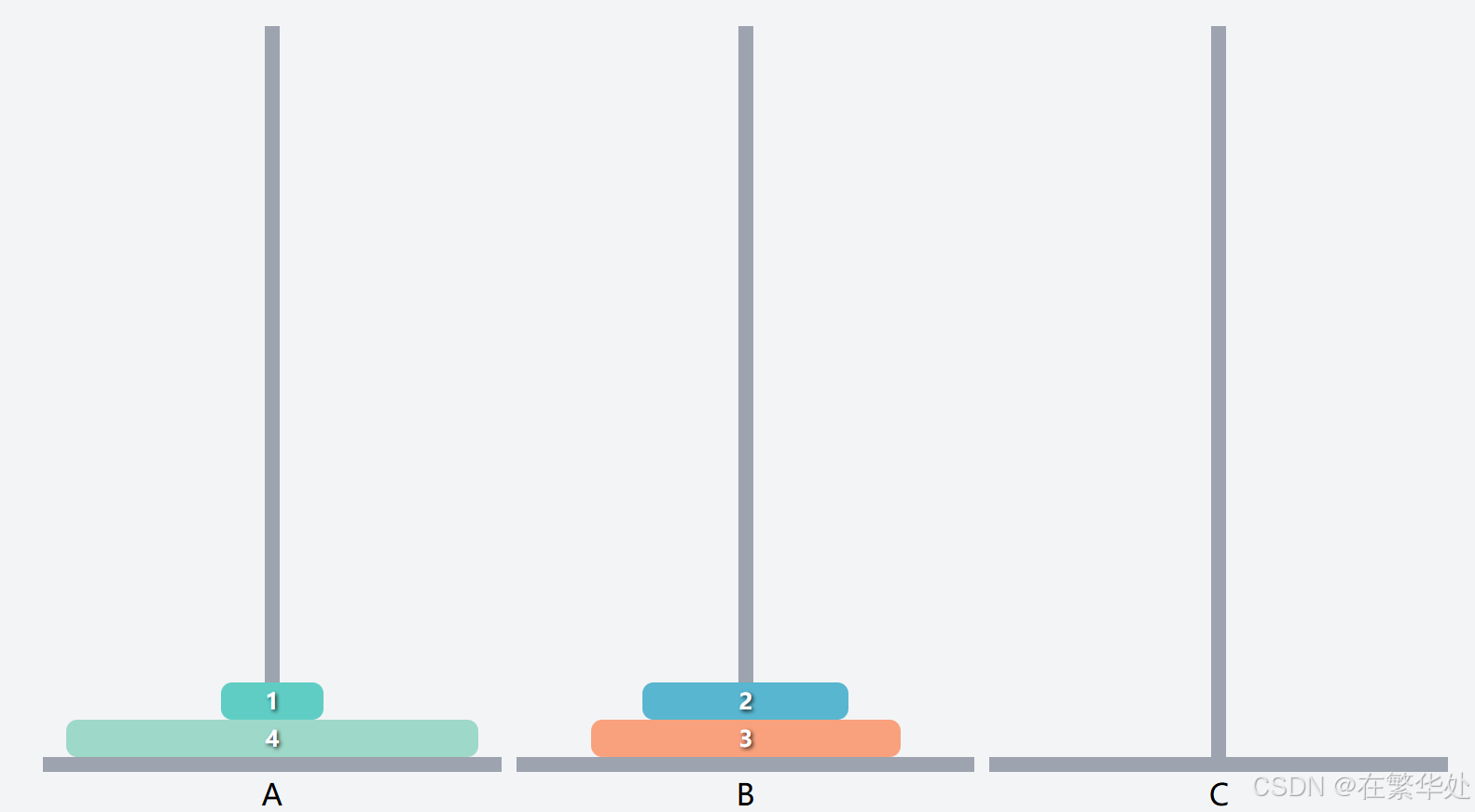
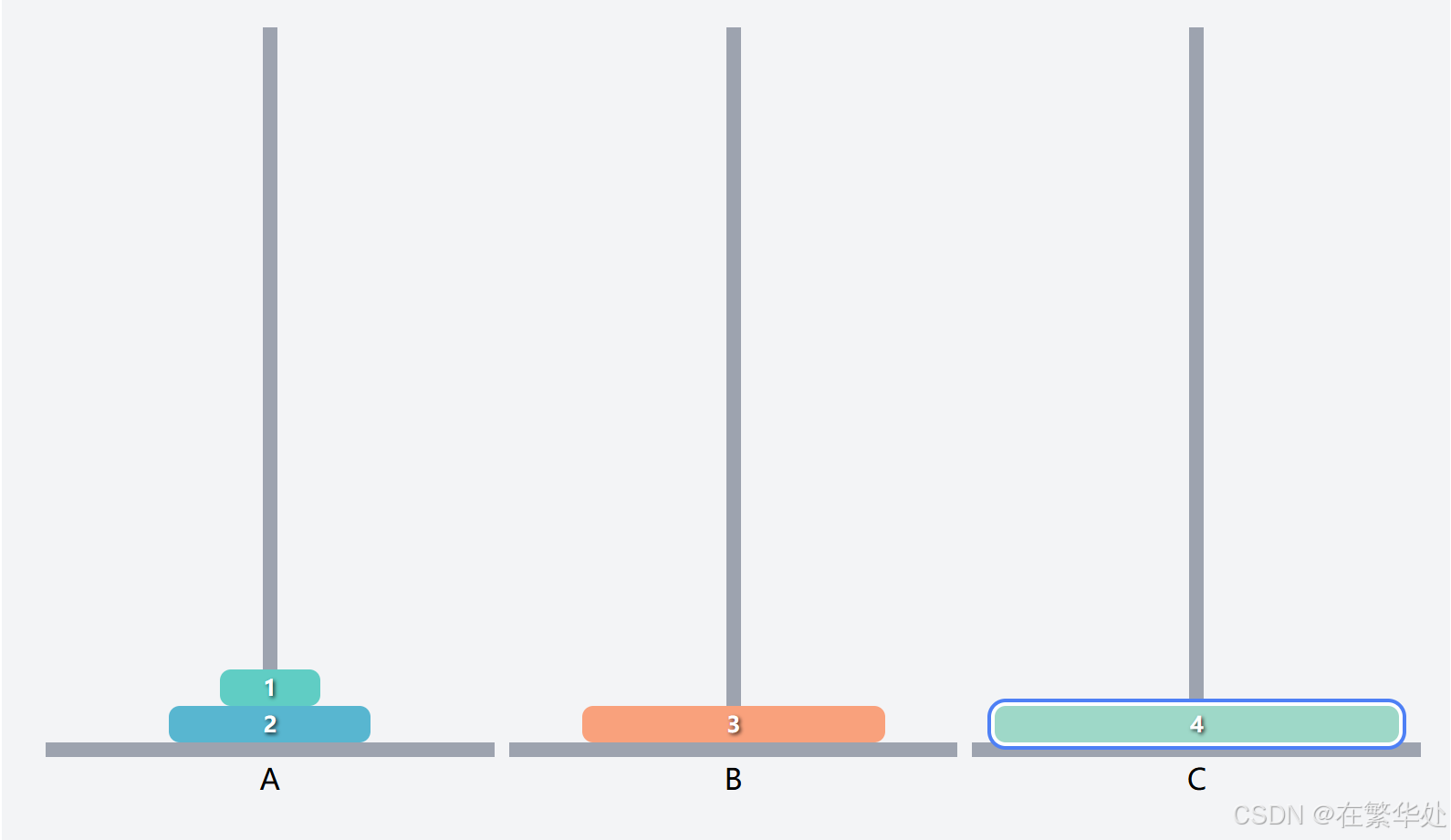
然后是将Q2(上两层)从起始柱A移动到目标柱C,这就需将序号1的盘子先移动到辅助B,再将序号2的盘子直接移动到目标柱C。
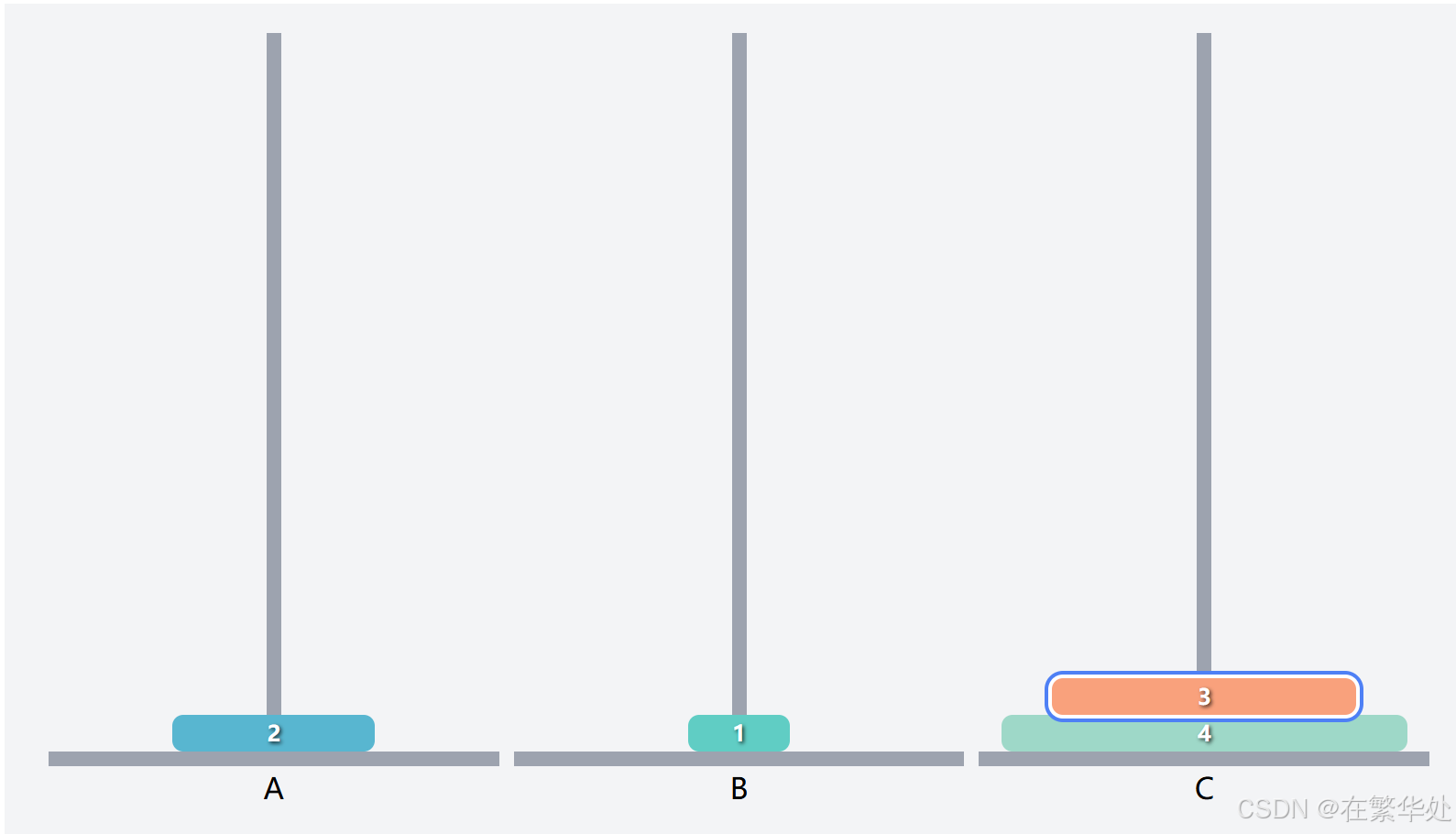
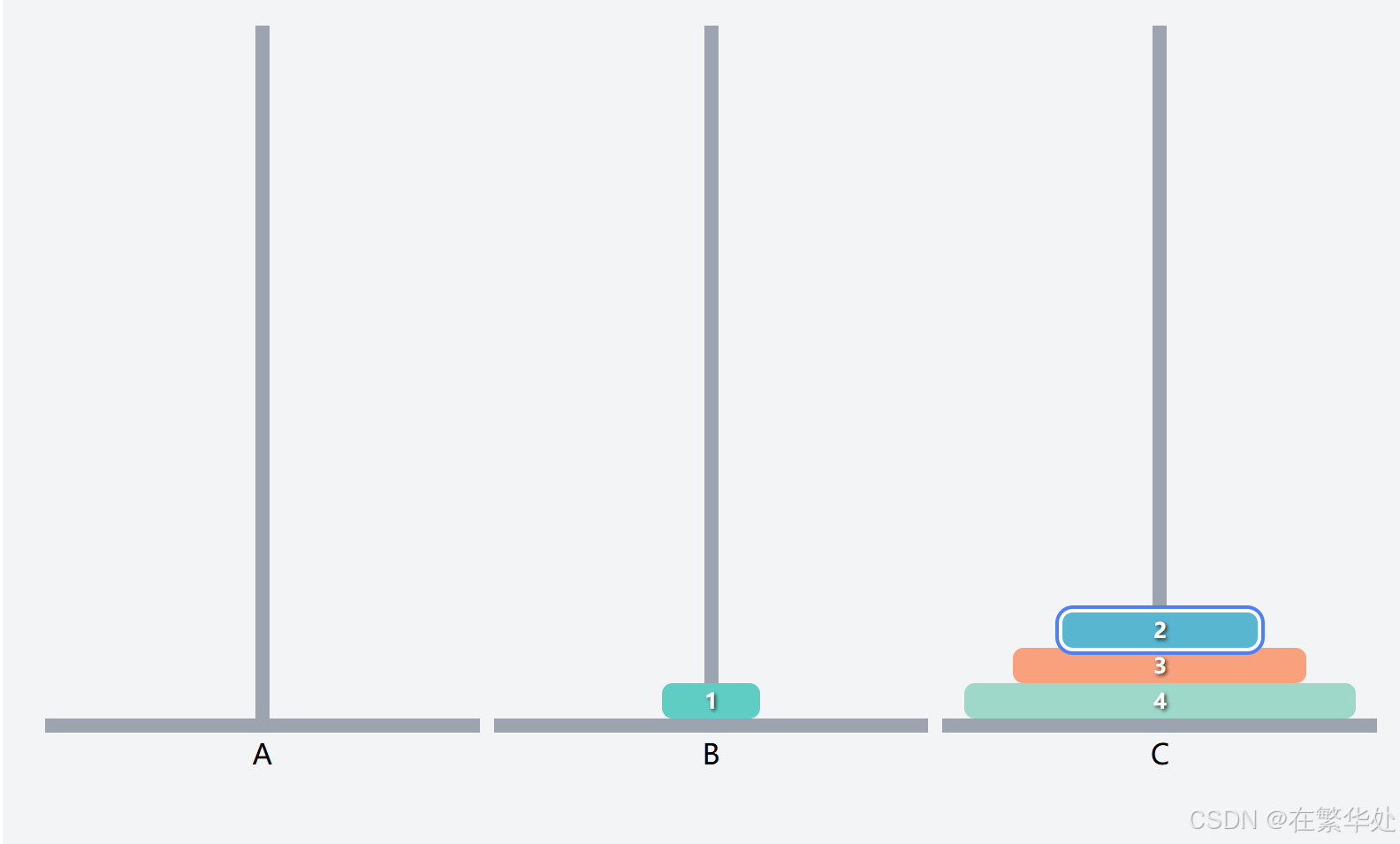
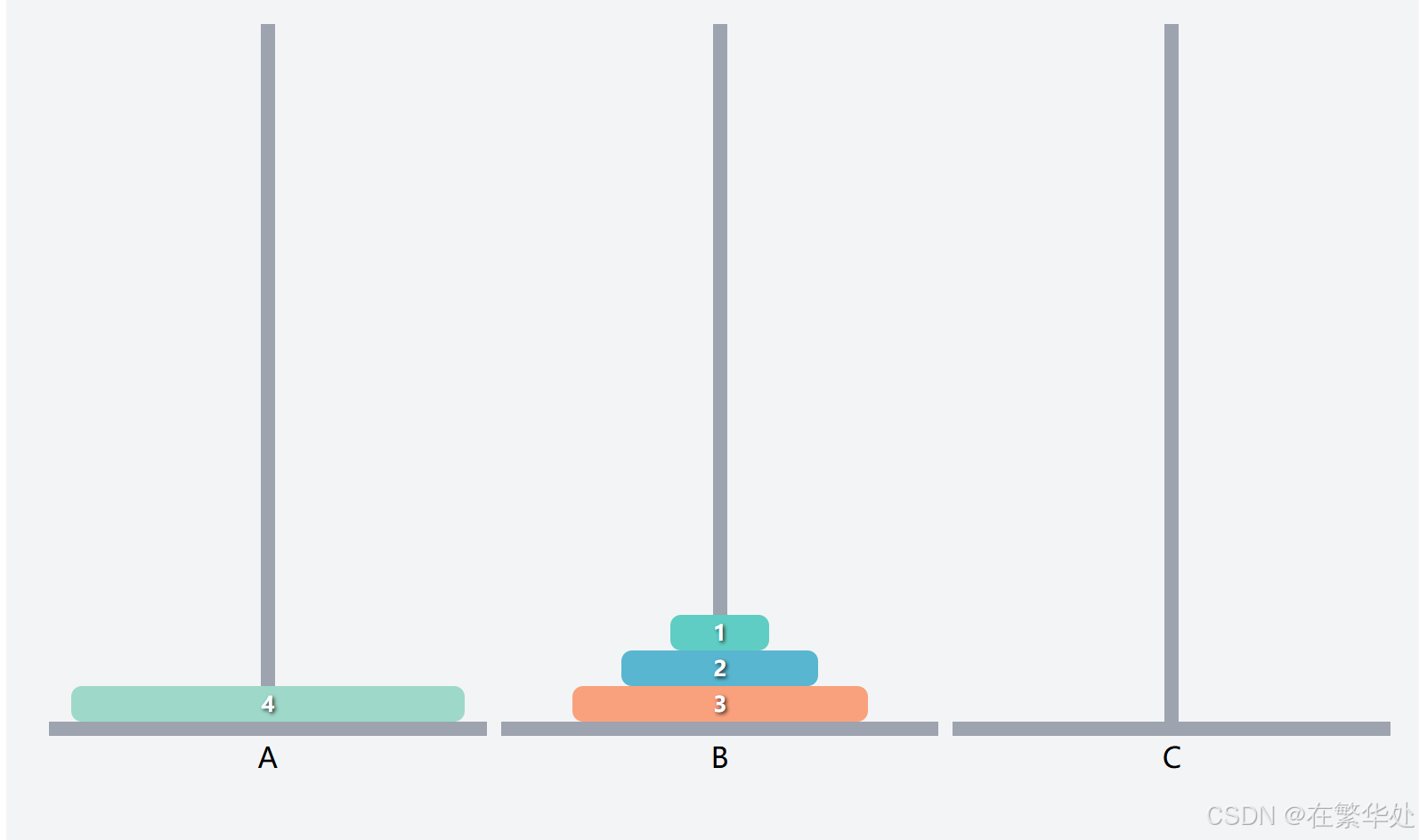
最后是将序号1的盘子直接移动到目标柱C。(强调这句是因为其不符合递归规律,属于条件判断的特例)

通过上述过程,我们不难发现此问题的灵魂在于把前n-1层看为一个整体,将复杂的问题转化为简单的两层问题,继而不断向前推。而我们只需加一个判断条件(n==1),使递归不断执行到最后两层为止。
这就是汉诺塔核心函数的含义:
函数hanoi()括号中的第一个位置表示要移动的数量,第二个位置表示起始柱,第三个位置表示辅助柱,第四个位置表示目标柱
void hanoi(int n, char pos1, char pos2, char pos3)
{
if (n == 1) move(pos1, pos3);
else
{
hanoi(n - 1, pos1, pos3, pos2);
move(pos1, pos3);//将第n层的盘子直接从pos1移动到pos3
hanoi(n - 1, pos2, pos1, pos3);
}
}
else{}中的代码作用即将前n-1层看成一个整体来执行新的汉诺塔问题(调换三种柱子的位置)
以下是汉诺塔问题的完整代码和4层汉诺塔操作步骤:
#include<stdio.h>
/**
* 移动盘子函数
* @param pos1 起始位置
* @param pos3 目标位置
*/
void move(char pos1, char pos3)
{
printf(" %c->%c ", pos1, pos3);
}
/**
* 汉诺塔递归解决函数
* @param n 盘子数量
* @param pos1 起始柱
* @param pos2 辅助柱
* @param pos3 目标柱
*/
void hanoi(int n, char pos1, char pos2, char pos3)
{
if (n == 1)
move(pos1, pos3);
else
{
hanoi(n - 1, pos1, pos3, pos2);
move(pos1, pos3);
hanoi(n - 1, pos2, pos1, pos3);
}
}
/**
* 主函数
*/
int main()
{
int n;
printf("请输入汉诺塔的盘子数: ");
scanf("%d", &n);
printf("移动步骤:\n");
hanoi(n, 'A', 'B', 'C');
printf("\n完成!\n");
return 0;
}



总结:
以上就是我的所有感悟了,感谢你的阅读,希望对你有所帮助。因为我也是刚接触此问题,所以难免有错误和疏漏的地方,欢迎大家的指正和批评。