Matlab创建传递函数，绘制零极点图1

题目：

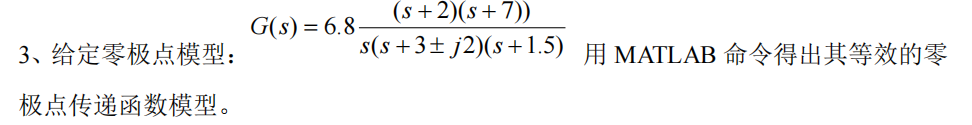
代码：

Matlab 复制代码

clc;clear all; close all;

num=6.8*conv([1,2],[1,7]);%定义分子
%定义分母
temp1=conv([1,0],[1,3+2*j]);
temp2=conv([1,3-2*j],[1,1.5]);
den=conv(temp1,temp2);

sys=tf(num,den);%创建传递函数

[z,p,k]=tf2zp(num,den);%求出零极点
sys_ep=zpk(z,p,k);

figure
pzmap(sys);
title('Pole-Zero Map');

%找到零极点
[z,p,~]=tf2zp(num,den);
%标注极点
for i=1:length(z)
    text(real(z(i)),imag(z(i)),['' num2str(z(i),'%.2f')],'Color','blue');
end
%标注极点
for i=1:length(p)
    text(real(p(i)),imag(p(i)),['' num2str(p(i),'%.2f')],'Color','red');
end

第一部分：环境准备与初始化

Matlab 复制代码

clc;
clear all;
close all;

这是 MATLAB 脚本的标准开场白，作用是清理工作环境，避免之前的工作对当前分析产生干扰。

clc;：清空命令窗口。擦除所有之前的输入命令和输出结果，让屏幕焕然一新，便于观察本次运行的结果。
clear all;：清除工作区。删除工作区中所有已定义的变量。这是一个非常重要的习惯，可以防止你在本次运行中不小心使用了上次遗留下来的旧变量，从而导致难以排查的错误。
close all;：关闭所有图形窗口。如果之前运行过绘图代码，可能会有多个 Figure 窗口打开。此命令会将它们全部关闭，确保本次代码绘制的图形是独立和干净的。

第二部分：构建传递函数的分子和分母

Matlab 复制代码

% 定义分子
num = 6.8 * conv([1,2],[1,7]);

% 定义分母
temp1 = conv([1,0],[1,3+2*j]);
temp2 = conv([1,3-2*j],[1,1.5]);
den = conv(temp1,temp2);

这部分是代码的核心，它通过多项式乘法（卷积）来构造传递函数的分子和分母。

分子 `num` 的构建

conv([1,2],[1,7])：conv 是 "卷积" 函数，在多项式运算中，它等价于多项式乘法 。
- [1, 2] 代表多项式 (s + 2)。
- [1, 7] 代表多项式 (s + 7)。
- 它们的卷积结果是 [1*1, 1*7 + 2*1, 2*7] = [1, 9, 14]，对应于多项式 (s+2)(s+7) = s² + 9s + 14。
num = 6.8 * ...：将上面得到的多项式乘以一个增益 6.8。
- 因此，分子多项式为 num(s) = 6.8 * (s² + 9s + 14)。

分母 `den` 的构建

分母的构建稍微复杂一些，它是三个多项式的乘积，所以分了几步进行。

temp1 = conv([1,0],[1,3+2*j]);
- [1, 0] 代表多项式 s。
- [1, 3+2*j] 代表多项式 (s + 3 + 2j)，其中 j 是 MATLAB 中的虚数单位。
- 乘积结果：temp1(s) = s * (s + 3 + 2j)。
temp2 = conv([1,3-2*j],[1,1.5]);
- [1, 3-2*j] 代表多项式 (s + 3 - 2j)，这是 (s + 3 + 2j) 的共轭复数。
- [1, 1.5] 代表多项式 (s + 1.5)。
- 乘积结果：temp2(s) = (s + 3 - 2j) * (s + 1.5)。
den = conv(temp1, temp2);
- 这是最后一步乘法，将 temp1 和 temp2 代表的多项式相乘。
- 最终分母多项式为 den(s) = s * (s + 3 + 2j) * (s + 3 - 2j) * (s + 1.5)。
- 注意：(s + 3 + 2j) * (s + 3 - 2j) 会产生一个实系数的二次项 (s² + 6s + 13)，这是因为共轭复数相乘会消去虚部。所以整个分母展开后是一个 4 阶的实系数多项式。

第三部分：创建系统模型并转换形式

Matlab 复制代码

sys = tf(num, den); % 创建传递函数

[z, p, k] = tf2zp(num, den); % 求出零极点
sys_ep = zpk(z, p, k);

这部分将上一步得到的多项式系数转化为 MATLAB 可以识别和分析的系统模型对象。

sys = tf(num, den);
- tf 是 "Transfer Function" 的缩写，用于创建一个传递函数模型。
- sys 现在是一个 tf 类型的对象，它内部存储了分子和分母的多项式系数。如果你在命令窗口输入 sys 并回车，MATLAB 会显示：
  Matlab 复制代码
```
sys =
       6.8 s^2 + 61.2 s + 95.2
---------------------------------------
s^4 + 7.5 s^3 + 22 s^2 + 39 s + 19.5
```
[z, p, k] = tf2zp(num, den);
- tf2zp 是 "Transfer Function to Zero-Pole" 的缩写，用于将传递函数从多项式形式 转换为零极点增益形式。
- 输出参数：
  - z (Zeros)：零点向量 。存储了分子多项式的根。对于我们的例子，z = [-7, -2]。
  - p (Poles)：极点向量 。存储了分母多项式的根。对于我们的例子，p = [-3+2j, -3-2j, -1.5, 0]。
  - k (Gain)：增益。系统的直流增益。对于我们的例子，k = 6.8。
sys_ep = zpk(z, p, k);
- zpk 用于创建一个零极点增益形式的系统模型。
- sys_ep 是一个 zpk 类型的对象。如果你在命令窗口输入 sys_ep，MATLAB 会显示：
  Matlab 复制代码
```
sys_ep =
       6.8 (s+7) (s+2)
---------------------------
s (s+1.5) (s^2 + 6s + 13)
```
- 这种形式更直观地展示了系统的零极点分布。

第四部分：绘制零极点图并进行标注

Matlab 复制代码

figure
pzmap(sys);
title('Pole-Zero Map');

% 找到零极点 (这一行有些重复，因为前面已经求过z和p了)
[z, p, ~] = tf2zp(num, den);

% 标注零点
for i = 1:length(z)
    text(real(z(i)), imag(z(i)), [' ' num2str(z(i),'%.2f')], 'Color', 'blue');
end

% 标注极点
for i = 1:length(p)
    text(real(p(i)), imag(p(i)), [' ' num2str(p(i),'%.2f')], 'Color', 'red');
end

这是代码的可视化与结果呈现部分，目的是生成一张清晰的零极点图。

figure：创建一个新的图形窗口，用于绘制接下来的图表。
pzmap(sys);：pzmap 是 "Pole-Zero Map" 的缩写，是绘制零极点图的专用函数。
- 它会在复平面（实轴为 x 轴，虚轴为 y 轴）上绘制出系统的所有零点和极点。
- 零点通常用 蓝色的圆圈 ○ 表示。
- 极点通常用 红色的叉号 × 表示。
title('Pole-Zero Map');：为图形添加一个标题。
[z, p, ~] = tf2zp(num, den);：注意，这一行代码在功能上是重复的。因为在第三部分我们已经通过 [z, p, k] = tf2zp(num, den); 计算出了 z 和 p。这里再次调用，虽然结果一样，但显得多余。可以直接使用之前计算好的 z 和 p。~ 是一个占位符，表示我们不关心第三个输出 k。
for 循环与 text 函数：这部分是代码的点睛之笔 ，它手动为每个零极点添加了数值标签，极大地增强了图形的可读性。
- for i = 1:length(z)：循环遍历所有零点。length(z) 给出了零点的数量。
- text(x, y, 'string', '属性', '值')：在图形的指定坐标 (x, y) 处添加文本 'string'。
- real(z(i)) 和 imag(z(i))：获取第 i 个零点的实部和虚部，并将其作为文本标注的 x 和 y 坐标，确保标签正好放在零极点的位置上。
- num2str(z(i),'%.2f')：将零点的数值（可能是复数）转换为字符串，并用 '%.2f' 格式化，保留两位小数。
- 'Color', 'blue' 或 'red'：将零点标签设为蓝色，极点标签设为红色，与 pzmap 的默认颜色保持一致。

实验结果：

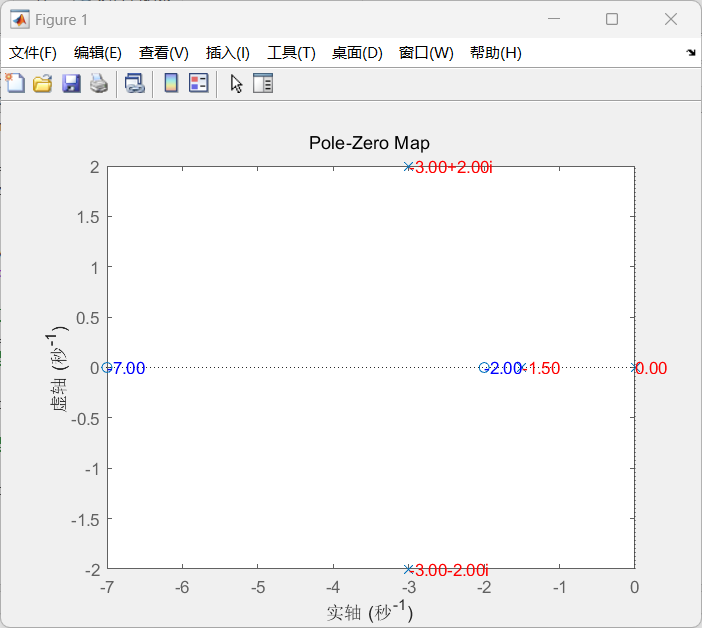
总结

总的来说，这是一段非常典型且实用的 MATLAB 控制工程分析代码。

优点：结构清晰，步骤完整，从模型构建到可视化分析一气呵成。特别是最后的 for 循环标注，展现了对图形定制的深入理解，是一个很好的实践。
可改进之处 ：
1. 代码中有一处重复计算 ：[z, p, ~] = tf2zp(num, den); 可以删除。

修正后的标注部分代码应为：

Matlab 复制代码

% 标注零点
for i = 1:length(z)
    text(real(z(i)), imag(z(i)), [' ' num2str(z(i),'%.2f')], 'Color', 'blue');
end

% 标注极点 (已修正)
for i = 1:length(p)
    text(real(p(i)), imag(p(i)), [' ' num2str(p(i),'%.2f')], 'Color', 'red');
end

Matlab创建传递函数，绘制零极点图1

题目：

代码：

第一部分：环境准备与初始化

第二部分：构建传递函数的分子和分母

分子 num 的构建

分母 den 的构建

第三部分：创建系统模型并转换形式

第四部分：绘制零极点图并进行标注

实验结果：

总结

分子 `num` 的构建

分母 `den` 的构建