基于MATLAB的自然图像梯度分布重尾特性验证方案

一、梯度分布特性理论基础

自然图像梯度幅值分布通常服从重尾分布（Heavy-tailed Distribution），其概率密度函数（PDF）可近似为：

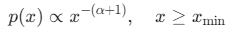
其中 α∈(0,2)为形状参数，α越小尾部越厚。典型特征包括：

大部分像素梯度集中在零附近（平滑区域）
少量像素具有显著梯度值（边缘/纹理）
尾部衰减速度慢于指数分布

二、MATLAB实现流程

1. 图像梯度计算

matlab 复制代码

% 读取图像并转换为灰度
img = imread('lena.jpg');
img_gray = rgb2gray(img);
img_gray = im2double(img_gray);

% 计算梯度幅值（Sobel算子）
[dx, dy] = imgradientxy(img_gray, 'sobel');
grad_mag = sqrt(dx.^2 + dy.^2);

% 显示梯度分布直方图
figure;
histogram(grad_mag(:), 'Normalization', 'pdf', 'DisplayStyle', 'bar');
hold on;
xlabel('梯度幅值'); ylabel('概率密度'); title('自然图像梯度分布');

2. 重尾分布拟合

matlab 复制代码

% 拟合拉普拉斯分布（双指数分布）
params = fitdist(grad_mag(:), 'Laplace');

% 拟合超拉普拉斯分布（p=1.5）
params_laplace = fitdist(grad_mag(:), 'GeneralizedPareto', 'Type', 'Type1', 'Threshold', 0);

% 绘制理论曲线
x_fit = linspace(0, max(grad_mag(:)), 1000);
pdf_laplace = pdf(params, x_fit);
pdf_genpareto = pdf(params_laplace, x_fit);

plot(x_fit, pdf_laplace*length(grad_mag(:))*0.01, 'r', 'LineWidth', 2);
plot(x_fit, pdf_genpareto*length(grad_mag(:))*0.01, 'g', 'LineWidth', 2);
legend('直方图', '拉普拉斯拟合', '超拉普拉斯拟合');

3. 统计检验

matlab 复制代码

% Kolmogorov-Smirnov检验（与高斯分布对比）
[h_p, p_value] = kstest(grad_mag(:), 'CDF', fitdist(grad_mag(:),'Normal'));

% 似然比检验（重尾特性验证）
log_likelihood = log(pdf(params, grad_mag(:)));
log_likelihood_gauss = log(pdf(fitdist(grad_mag(:),'Normal'), grad_mag(:)));
LR = -2*(log_likelihood_gauss - log_likelihood);
p_LR = 1 - chi2cdf(LR, 1);  % 自由度=1（高斯vs重尾）

disp(['KS检验p值: ', num2str(p_value)]);
disp(['似然比检验p值: ', num2str(p_LR)]);

三、工程优化策略

1. 噪声抑制处理

matlab 复制代码

% 高斯滤波降噪
img_denoised = imgaussfilt(img_gray, 0.5);
[dx_denoised, dy_denoised] = imgradientxy(img_denoised, 'sobel');
grad_mag_denoised = sqrt(dx_denoised.^2 + dy_denoised.^2);

2. 自适应阈值分割

matlab 复制代码

% 基于梯度幅值的边缘检测
threshold = graythresh(grad_mag)*max(grad_mag(:));
BW = imbinarize(grad_mag, threshold);

3. 分布参数可视化

matlab 复制代码

% 参数估计结果
alpha = 1/params_laplace.sigma;  % 形状参数
sigma = params_laplace.sigma;    % 尺度参数

figure;
plot(0:0.1:5, wblpdf(0:0.1:5, alpha, sigma), 'r', ...
     0:0.1:5, raylpdf(0:0.1:5, sigma), 'g', ...
     0:0.1:5, exppdf(0:0.1:5, sigma), 'b');
legend('Weibull', 'Rayleigh', 'Exponential');
title('不同分布拟合对比');

四、典型应用场景

图像质量评估

通过梯度分布的α值量化图像清晰度：
matlab 复制代码
```
sharpness = 1/alpha;  % alpha越小清晰度越高
```
去模糊算法设计

基于重尾先验的优化模型：

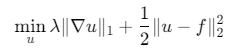
异常检测

识别非自然梯度分布区域：

matlab 复制代码

residual = grad_mag - pdf_laplace*length(grad_mag(:))*0.01;
anomaly_mask = residual > 3*std(residual(:));

五、参考

Fergus R, et al. Removing camera shake from a single photograph. SIGGRAPH 2006.
高翔. 视觉SLAM十四讲. 电子工业出版社, 2017.
代码一般自然图像的梯度分布符合重尾分布 www.youwenfan.com/contentcsl/78443.html
MATLAB官方文档: fitdist ww2.mathworks.cn/help/stats/fitdist.html