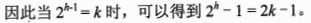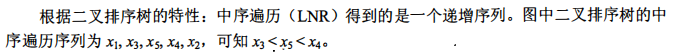目录
核心问题：在数组中寻找缺失的最小正整数，需忽略负数和零，仅关注正整数范围
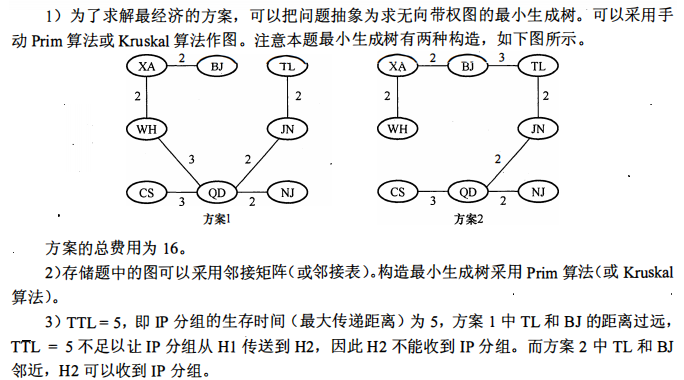
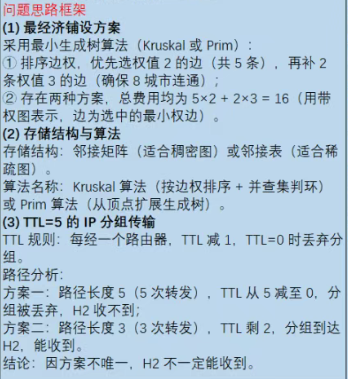
核心问题：求解无向带权图的最小生成树（即连接所有结点且总权值最小的子图）
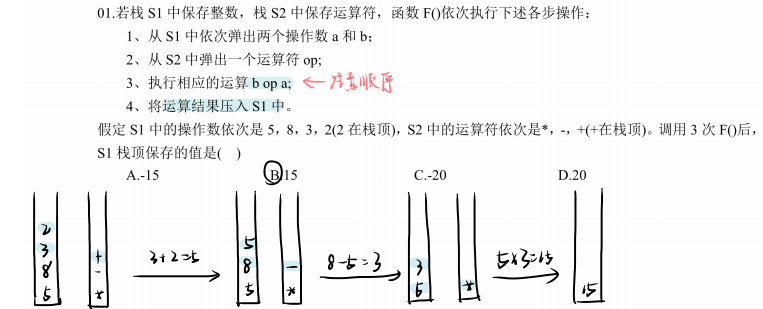
考察栈、后进先出
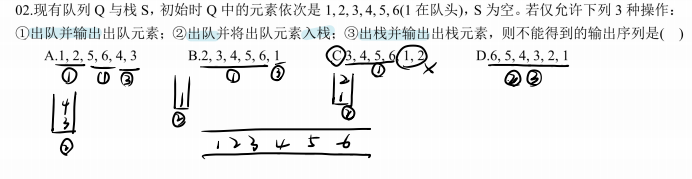
考察队列和栈
A.1，2出队输出；3，4入栈；5，6出队输出，再出栈4,3；可行
B.1入栈；2,3,4,5,6出队输出，再出栈1；可行
C.1,2入栈；3,4,5,6出队输出；无法得到1,2
D.1~5入栈；6出队输出；再出栈1~5
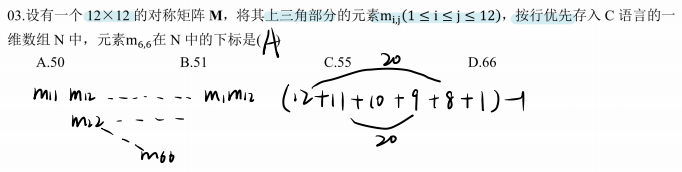
考察对称矩阵上三角存储的下标计算方法；矩阵压缩存储
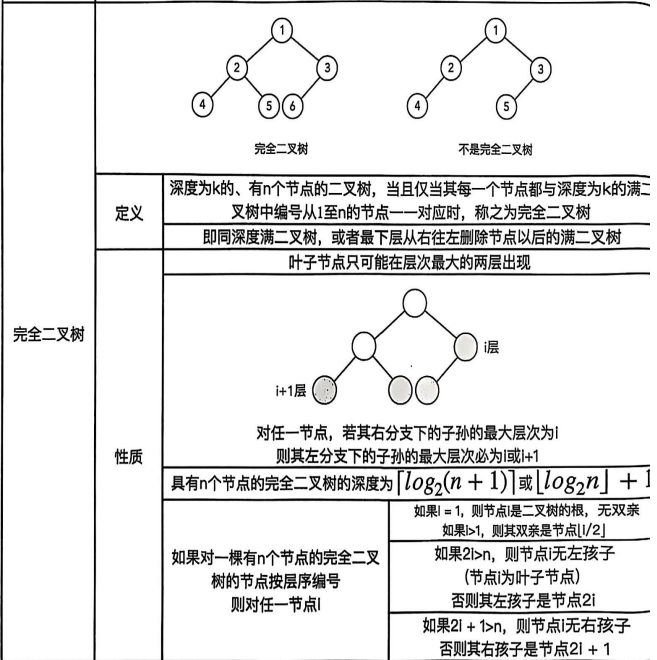
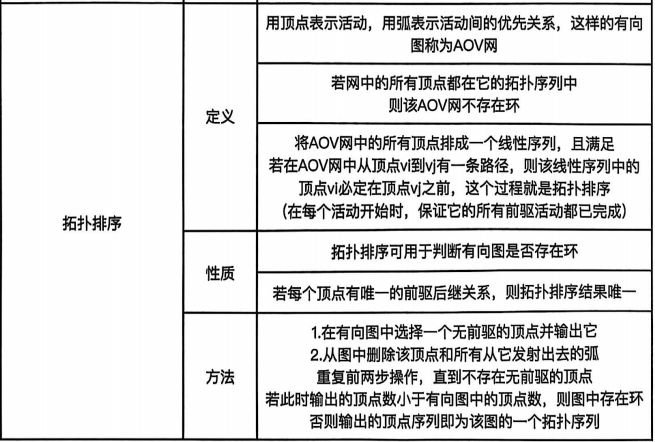
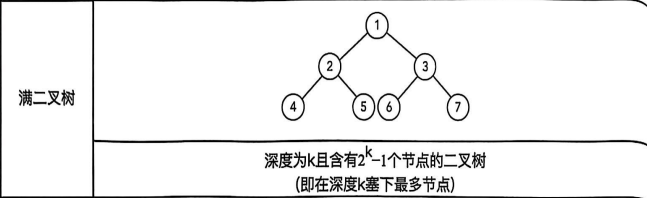
考察完全二叉树的结构特征，叶子结点与非叶子结点
非叶子结点的度均为2，且所有叶结点都位于同一层的完全二叉树就是慢二叉树。对应一棵高度为h的满二叉树（空树h=0），其最后一层全部是叶结点，数量为
，总结点数为
完全二叉树性质：叶结点同层，非叶结点均有2子结点，w为满二叉树
叶结点数
总结点n=
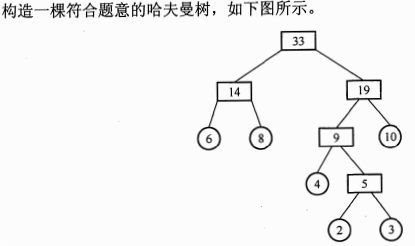
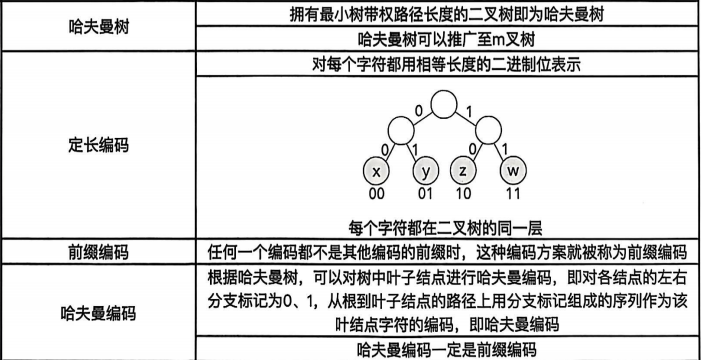
考察哈夫曼树的构造过程和编码规则；前缀编码
哈夫曼编码特性：前缀编码，频率高的字符编码短
2（d）、3（b）、4（f）、6（a）、8（c）、10（e），每次合并最小两节点
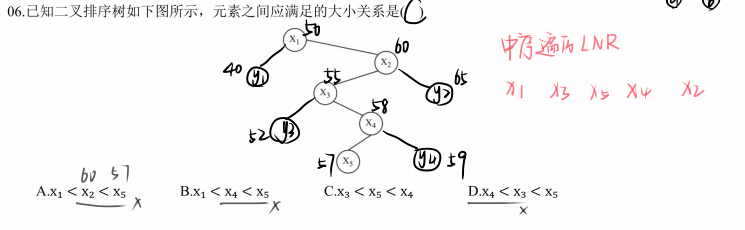
考察二叉排序树（BST）的性质；结点值大小关系
二叉排序树性质：中序遍历为递增序列
中序遍历序列：左子树
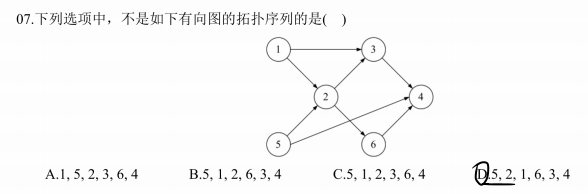
考察拓扑排序；有向图拓扑序列的生成
拓扑排序每次选取入度为0的结点输出
考察B树的结构特性；不同高度下关键字数量下限
3阶B树：非根结点至少有
高度为5的关键字个数：
第1层（根）：1个关键字
第2层：2个结点，各1关键字，共2个
第3层：4个结点，各1个，共4个
第4层：8个结点，各1个，共8个
第5层（叶）：16个结点，各1个，共16个
总和=1+2+4+8+16=31
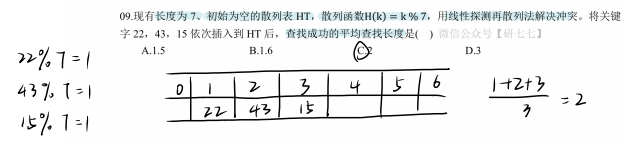
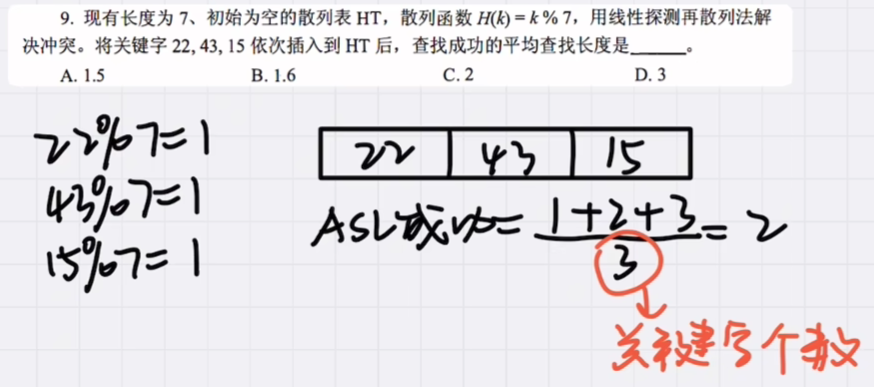
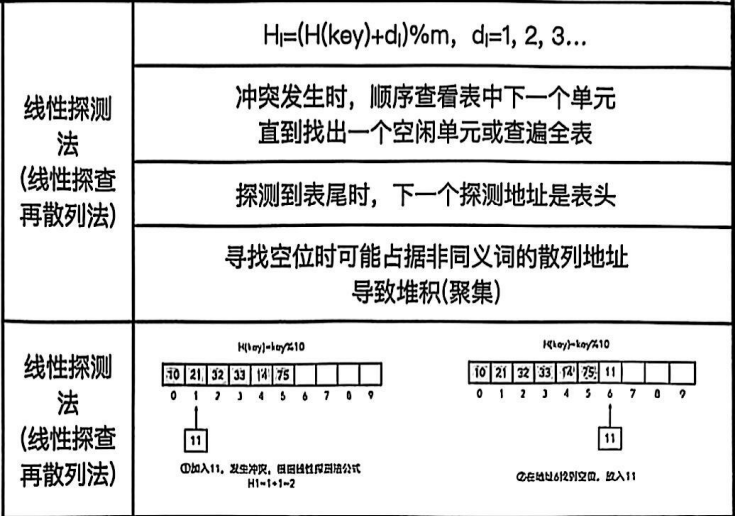
考察散列函数和冲突解决策略；查找长度计算
散列表插入过程：
22%7=1，直接插入HT1，查找长度1
43%7=1（冲突），线性探测HT2，查找长度2
15%7=1（冲突），探测HT2（冲突），HT3，查找长度3
平均查找长度=(1+2+3)/3=2
查找到空单元，才能确定是失败了
成功的时候，对象是关键字，去看每个关键字比较多少次
失败的时候。对象是映射的这个范围的地址，拿这个地址去看一下每个地址如果找不到关键字需要比多少次（当前这个地址到空单元需要多少次）
考察希尔排序的增量选择策略；排序过程中增量变化
希尔排序特征：按增量d分组排序，使序列"间隔有序"
把待排序表相隔几个元素分割成几个子表
对每个子表分别进行直接插入排序
整个表中的元素已基本有序时，再对全体记录进行一次插入排序
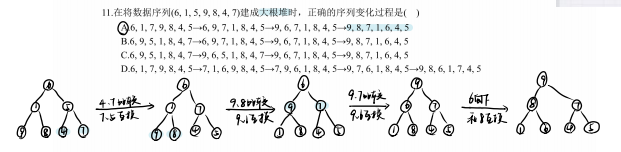
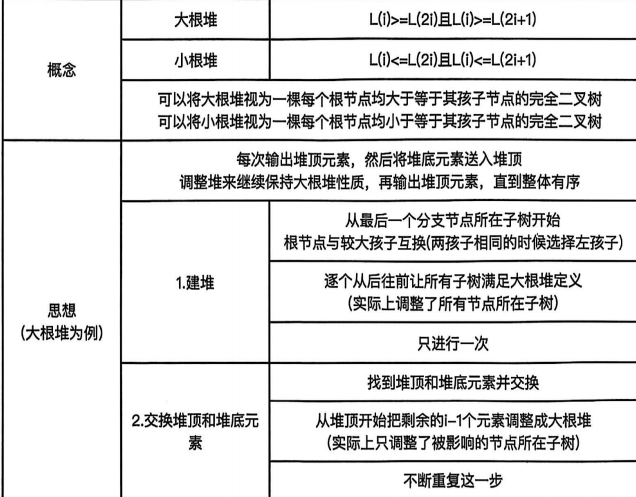
考察堆排序中建堆的过程；大根堆调整步骤和结点交换逻辑大根堆：父
大根堆是完全二叉树
从最后一个非叶子结点（下标3，值为5）：其左孩子（下标6，值4），右孩子（下标7，值7）；因为7>5，交换5和7，序列变为(6,1,7,9,8,4,5)
下一个非叶子结点（下标2，值1）：左孩子（下标4，值9），右孩子（下标5，值8）；因为9>1且9>8，交换1和9，序列变为(6,9,7,1,8,4,5)
调整根结点（下标1，值6）：左孩子（下标2，值9），右孩子（下标3，值7）；因为9>6且9>7，交换6和9，序列变为(9,6,7,1,8,4,5)
再次调整根结点子树（交换后需检查子树是否满足大根堆）：下标2值为6，其左右孩子下标4值1、下标5值8；因为8>6，交换6和8，序列变为(9,8,7,1,6,4,5)
核心问题：在数组中寻找缺失的最小正整数，需忽略负数和零，仅关注正整数范围
思路：
排序法：将数组排序后遍历，从1开始检查每个正整数是否存在
哈希表法：用哈希结合记录出现的正整数，再从1开始查找缺失值
原地置换法：最后通过交换元素，将每个正整数放到对应索引位置，最后遍历数组检查缺失的位置
核心问题：求解无向带权图的最小生成树（即连接所有结点且总权值最小的子图）
最小生成树算法：
Kruskal算法：按边权排序，用并查集避免环，依次选边
Prim算法：从某结点出发，逐步添加相邻最小权边
图的存储结构：
邻接矩阵：适合稠密图，查询边权时间为O(1)
邻接表：适合稀疏图，存储效率高
最小生成树可能不唯一
