5G系统的带宽远大于4G,为了满足不同能力终端的接入NR提出了BWP的概念,即将整个小区带宽划分成不同子带宽,从而满足不同UE的接入。然而基站在发送的时候一般是以小区的中心频点进行上变频和下变频。UE是在自己接入的带宽中心频点进行上下变频且不知道基站的中心频点。这就导致基站和终端的中心载频不一致,从而引入了一个相位偏差。
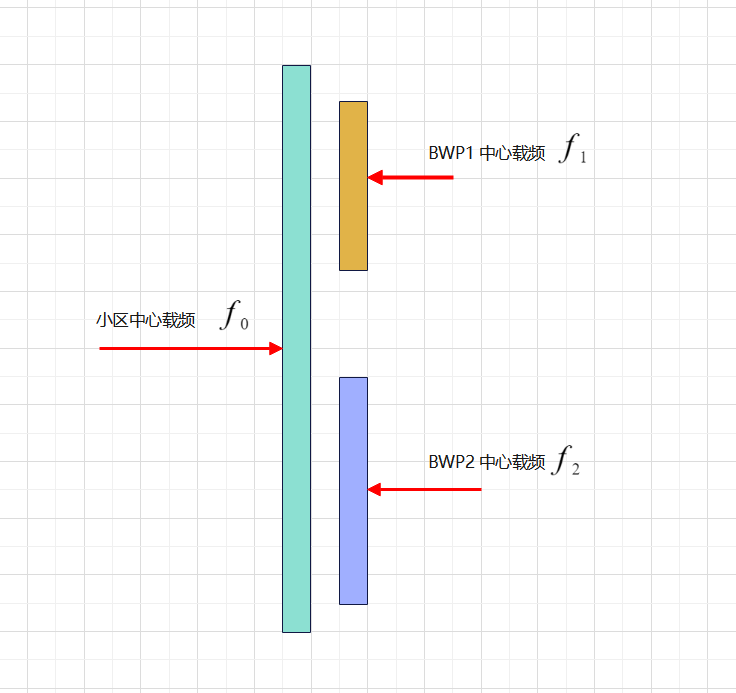
假设OFDM基带信号表示为slp,μ(t)s_{l}^{p,\mu}(t)slp,μ(t),RF已f0f_{0}f0进行上变频,上变频后的信号可表示为slp,u(t)ej2f0ts_{l}^{p,u}(t)e^{j2f_{0}t}slp,u(t)ej2f0t。基站通过天线端口将信号发射出去,终端接收到该信号后进行下变频。假设终端已f1f_{1}f1进行下变频,变频后的基带信号可表示为:
slp,μ(t)ej2(f0−f1)t s_{l}^{p,\mu}(t)e^{j2(f_{0}-f_{1})t} slp,μ(t)ej2(f0−f1)t
3GPP上变频公式如下:
Re{sl(t)⋅ej2πfTXt}⇒Re{sl(p,μ)(t)⋅ej2πf0(t−TcNCP,lμ)} \mathcal{Re}\left\{s_{l}(t)\cdot e^{j2\pi f_{TX}t} \right\}\Rightarrow \mathcal{Re}\left\{s_{l}^{(p,\mu)}(t)\cdot e^{j2\pi f_{0}(t-T_{c}N_{CP,l}^{\mu})} \right\} Re{sl(t)⋅ej2πfTXt}⇒Re{sl(p,μ)(t)⋅ej2πf0(t−TcNCP,lμ)}
Common 参数
sl(p,μ)(t)=∑k=0Ngrid,xsize,μNscRB−1ak,l(p,μ) e j2π(k+k0μ−Ngrid,xsize,μNscRB/2)Δf(t−NCP,lμTc) s_{l}^{(p,\mu)}(t) = \sum_{k=0}^{N_{\text{grid},x}^{\text{size},\mu}N_{\text{sc}}^{\text{RB}}-1} a_{k,l}^{(p,\mu)} \, e^{\, j2\pi \left( k + k_{0}^{\mu} - N_{\text{grid},x}^{\text{size},\mu}N_{\text{sc}}^{\text{RB}}/2 \right) \Delta f \left( t - N_{\text{CP},l}^{\mu}T_{c} \right) } sl(p,μ)(t)=k=0∑Ngrid,xsize,μNscRB−1ak,l(p,μ)ej2π(k+k0μ−Ngrid,xsize,μNscRB/2)Δf(t−NCP,lμTc)
发送波形(窗函数)
wlμ(t)={1,0≤t≤(Nuμ+NCP,lμ)Tc0,otherwise w_{l}^{\mu}(t) = \begin{cases} 1, & 0 \leq t \leq (N_{u}^{\mu} + N_{CP,l}^{\mu}) T_{c} \\ 0, & \text{otherwise} \end{cases} wlμ(t)={1,0,0≤t≤(Nuμ+NCP,lμ)Tcotherwise
tstart,l=∑l′=0l−1(Nuμ+NCP,lμ)Tc t_{\text{start},l} = \sum_{l'=0}^{l-1} (N_{u}^{\mu} + N_{CP,l}^{\mu}) T_{c} tstart,l=l′=0∑l−1(Nuμ+NCP,lμ)Tc
基站相位补偿
sl(p,μ)⋅e−jϕl=∑k=0Ngrid,xsize,μNscRB−1ak,l(p,μ) e j2π(k+k0μ−Ngrid,xsize,μNscRB/2)Δf(t−NCP,lμTc)⋅e−jϕlϕl=2πf0(TcNCP,lμ+tstart,l)phase term that need to be multiplied to OFDM symbol \begin{align*} s_{l}^{(p,\mu)}\cdot \colorbox{yellow}{\\displaystyle e\^{-j\\phi_{l}}}&=\sum_{k=0}^{N_{\text{grid},x}^{\text{size},\mu}N_{\text{sc}}^{\text{RB}}-1} a_{k,l}^{(p,\mu)} \, e^{\, j2\pi \left( k + k_{0}^{\mu} - N_{\text{grid},x}^{\text{size},\mu}N_{\text{sc}}^{\text{RB}}/2 \right) \Delta f \left( t - N_{\text{CP},l}^{\mu}T_{c} \right) }\cdot \colorbox{yellow}{\\displaystyle e\^{-j\\phi_{l}}}\\ \phi_{l}&=2\pi f_{0}(T_{c}N_{CP,l}^{\mu}+t_{start,l})\\ &\colorbox{yellow}{\text{phase term that need to be multiplied to OFDM symbol}} \end{align*} sl(p,μ)⋅e−jϕlϕl=k=0∑Ngrid,xsize,μNscRB−1ak,l(p,μ)ej2π(k+k0μ−Ngrid,xsize,μNscRB/2)Δf(t−NCP,lμTc)⋅e−jϕl=2πf0(TcNCP,lμ+tstart,l)phase term that need to be multiplied to OFDM symbol
gnb Up-conversion aignal waveform
x(p,μ)(t)=Re{(∑lwlμ(t−tstart,l)sl(p,μ)(t−tstart,l)⋅e−j2πf0(tstart,l+NCP,lμTc)⏟gnb phase pre-compensation )⋅ej2πf0(t)}=∑lwlμ(t−tstart)Re{sl(p,μ)(t−tstart,l)⋅e2πf0(t−NCP,lμTc−tstart,l)} \begin{align*} x^{(p,\mu)}(t)&=\mathcal{Re}\left\{ \left (\sum_{l}w_{l}^{\mu}(t-t_{start,l})s_{l}^{(p,\mu)}(t-t_{start,l})\cdot \underbrace{\colorbox{yellow}{\\displaystyle e\^{-j2\\pi f_{0}(t_{start,l}+N_{CP,l}\^{\\mu}T_{c})}}}{\text{gnb phase pre-compensation }} \right) \cdot e^{j2\pi f{0}(t)} \right\}\\ &=\sum_{l}w_{l}^{\mu}(t-t_{start})\mathcal{Re}\left\{s_{l}^{(p,\mu)}(t-t_{start,l})\cdot e^{2\pi f_{0}(t-N_{CP,l}^{\mu} T_{c}-t_{start,l}}) \right\}\\ \end{align*} x(p,μ)(t)=Re⎩ ⎨ ⎧ l∑wlμ(t−tstart,l)sl(p,μ)(t−tstart,l)⋅gnb phase pre-compensation e−j2πf0(tstart,l+NCP,lμTc) ⋅ej2πf0(t)⎭ ⎬ ⎫=l∑wlμ(t−tstart)Re{sl(p,μ)(t−tstart,l)⋅e2πf0(t−NCP,lμTc−tstart,l)}
UE-Down-conversion signal waveform
x^l(p,μ)(t)=xl(p,μ)(t+tstart,l)⋅e−j2πf1(t−tstart,l),0≤t≤(Nuμ+NCP,lμTc)⇓x^l(p,μ)(t)⋅ej2πf1(tstart,l+NCP,lμTc)⏟ue phase compensation=(sl(p,μ)(t)⋅e−2πf0(tstart,l+NCP,lμTc)⏟gnb phase compensation⋅ej2πf0(t−tstart,l))⋅(ej2πf1(tstart,l+NCP,lμTc)⏟ue phase compensation⋅e−j2πf1(t−tstart,l))⇓=sl(p,μ)(t)⋅e2π(f0−f1)(t−tstart,l)⋅e−2π(f0−f1)tstart,l⋅e−2π(f0−f1)NCP,lμTc=sl(p,μ)⋅e2π(f0−f1)t⋅e−2π(f0−f1)NCP,lμTc=sl(p,μ)⋅e2π(f0−f1)(t−NCP,lμ) \begin{align*} \hat{x}{l}^{(p,\mu)}(t)&=x{l}^{(p,\mu)}(t+t_{start,l})\cdot \colorbox{yellow}{\\displaystyle e\^{-j2\\pi f_{1}(t-t_{start,l})}},0\leq t\leq(N_{u}^{\mu}+N_{CP,l}^{\mu}T_{c})\\ &\Downarrow\\ \hat{x}{l}^{(p,\mu)}(t)\cdot \underbrace{\colorbox{yellow}{e\^{j2\\pi f_{1}(t_{start,l}+N_{CP,l}\^{\\mu}T_{c})}}}{\text{ue phase compensation}}&=\left( s_{l}^{(p,\mu)}(t)\cdot \underbrace{\colorbox{yellow}{e\^{-2\\pi f_{0}(t_{start,l}+N_{CP,l}\^{\\mu}T_{c})} }}{\text{gnb phase compensation}}\cdot e^{j2\pi f{0}(t-t_{start,l})} \right)\cdot \left(\underbrace{\colorbox{yellow}{e\^{j2\\pi f_{1}(t_{start,l}+N_{CP,l}\^{\\mu}T_{c})}}}{\text{ue phase compensation}}\cdot \colorbox{yellow}{\\displaystyle e\^{-j2\\pi f_{1}(t-t_{start,l})}}\right)\\ &\Downarrow\\ &=s{l}^{(p,\mu)}(t)\cdot e^{2\pi (f_{0}-f_{1})(t-t_{start,l})}\cdot e^{-2\pi(f_{0}-f_{1})t_{start,l} }\cdot e^{-2\pi (f_{0}-f_{1})N_{CP,l}^{\mu}T_{c}}\\ &=s_{l}^{(p,\mu)}\cdot e^{2\pi (f_{0}-f_{1})t}\cdot e^{-2\pi (f_{0}-f_{1})N_{CP,l}^{\mu}T_{c}}\\ &=s_{l}^{(p,\mu)}\cdot e^{2\pi (f_{0}-f_{1})(t-N_{CP,l}^{\mu})}\\ \end{align*} x^l(p,μ)(t)x^l(p,μ)(t)⋅ue phase compensation ej2πf1(tstart,l+NCP,lμTc)=xl(p,μ)(t+tstart,l)⋅e−j2πf1(t−tstart,l),0≤t≤(Nuμ+NCP,lμTc)⇓= sl(p,μ)(t)⋅gnb phase compensation e−2πf0(tstart,l+NCP,lμTc)⋅ej2πf0(t−tstart,l) ⋅ ue phase compensation ej2πf1(tstart,l+NCP,lμTc)⋅e−j2πf1(t−tstart,l) ⇓=sl(p,μ)(t)⋅e2π(f0−f1)(t−tstart,l)⋅e−2π(f0−f1)tstart,l⋅e−2π(f0−f1)NCP,lμTc=sl(p,μ)⋅e2π(f0−f1)t⋅e−2π(f0−f1)NCP,lμTc=sl(p,μ)⋅e2π(f0−f1)(t−NCP,lμ)
又
sl(p,μ)(t)=∑k=0Ngrid,xsize,μNscRB−1ak,l(p,μ) e j2π(k+k0μ−Ngrid,xsize,μNscRB/2)Δf(t−NCP,lμTc) s_{l}^{(p,\mu)}(t) = \sum_{k=0}^{N_{\text{grid},x}^{\text{size},\mu}N_{\text{sc}}^{\text{RB}}-1} a_{k,l}^{(p,\mu)} \, e^{\, j2\pi \left( k + k_{0}^{\mu} - N_{\text{grid},x}^{\text{size},\mu}N_{\text{sc}}^{\text{RB}}/2 \right) \Delta f \left( t - N_{\text{CP},l}^{\mu}T_{c} \right) } sl(p,μ)(t)=k=0∑Ngrid,xsize,μNscRB−1ak,l(p,μ)ej2π(k+k0μ−Ngrid,xsize,μNscRB/2)Δf(t−NCP,lμTc)
所以:
sl(p,μ)(t)=∑k=0Ngrid,xsize,μNscRB−1ak,l(p,μ) e j2π(k+k0μ−Ngrid,xsize,μNscRB/2)Δf(t−NCP,lμTc)⋅e2π(f0−f1)(t−NCP,lμ)⇓sl(p,μ)(t)=∑k=0Ngrid,xsize,μNscRB−1ak,l(p,μ) e j2π(k+k0μ−Ngrid,xsize,μNscRB/2+f0−f1Δf⏟offset sub carrier)Δf(t−NCP,lμTc) \begin{align*} s_{l}^{(p,\mu)}(t) &= \sum_{k=0}^{N_{\text{grid},x}^{\text{size},\mu}N_{\text{sc}}^{\text{RB}}-1} a_{k,l}^{(p,\mu)} \, e^{\, j2\pi \left( k + k_{0}^{\mu} - N_{\text{grid},x}^{\text{size},\mu}N_{\text{sc}}^{\text{RB}}/2 \right) \Delta f \left( t - N_{\text{CP},l}^{\mu}T_{c} \right) }\cdot e^{2\pi (f_{0}-f_{1})(t-N_{CP,l}^{\mu})}\\ &\Downarrow\\ s_{l}^{(p,\mu)}(t) &= \sum_{k=0}^{N_{\text{grid},x}^{\text{size},\mu}N_{\text{sc}}^{\text{RB}}-1} a_{k,l}^{(p,\mu)} \, e^{\, j2\pi \left( k + k_{0}^{\mu} - N_{\text{grid},x}^{\text{size},\mu}N_{\text{sc}}^{\text{RB}}/2 + \underbrace {\colorbox{yellow}{\\frac{f_{0}-f_{1}}{\\Delta f}}}{\text{offset sub carrier}} \right) \Delta f \left( t - N{\text{CP},l}^{\mu}T_{c} \right) }\\ \end{align*} sl(p,μ)(t)sl(p,μ)(t)=k=0∑Ngrid,xsize,μNscRB−1ak,l(p,μ)ej2π(k+k0μ−Ngrid,xsize,μNscRB/2)Δf(t−NCP,lμTc)⋅e2π(f0−f1)(t−NCP,lμ)⇓=k=0∑Ngrid,xsize,μNscRB−1ak,l(p,μ)ej2π(k+k0μ−Ngrid,xsize,μNscRB/2+offset sub carrier Δff0−f1)Δf(t−NCP,lμTc)
示例


总结:NR 系统中相位补偿在基站和UE分别进行,每个符号的补偿值是固定的,如上示例15KHZ子载波间隔下所有符号都是一样的 :
ej2πf1(tstart,l+NCP,lμTc)⏟ue phase compensatione−2πf0(tstart,l+NCP,lμTc)⏟gnb phase compensationtstart,l=∑l′=0l−1(Nuμ+NCP,lμ)Tc \underbrace{\colorbox{yellow}{e\^{j2\\pi f_{1}(t_{start,l}+N_{CP,l}\^{\\mu}T_{c})}}}{\text{ue phase compensation}}\\ \underbrace{\colorbox{yellow}{e\^{-2\\pi f_{0}(t_{start,l}+N_{CP,l}\^{\\mu}T_{c})} }}{\text{gnb phase compensation}}\\ t_{\text{start},l} = \sum_{l'=0}^{l-1} (N_{u}^{\mu} + N_{CP,l}^{\mu}) T_{c} ue phase compensation ej2πf1(tstart,l+NCP,lμTc)gnb phase compensation e−2πf0(tstart,l+NCP,lμTc)tstart,l=l′=0∑l−1(Nuμ+NCP,lμ)Tc
1\]https://www.3gpp.org/ftp/TSG_RAN/WG1_RL1/TSGR1_AH/NR_AH_1801/Docs/R1-1800296 \[2\] Overview of OFDM Phase Compensation in 5G NR Communication Systems \[3\]3GPP-38.211.5.3,3GPP-38.211.5.4 \[4\] PAPR Reduction Using Iterative Clipping/Filtering and ADMM Approaches for OFDM-Based Mixed-Numerology Systems