学习参考:《labuladong 的算法笔记》
https://labuladong.online/algo/data-structure-basic/graph-basic/#邻接表和邻接矩阵实现图结构
一幅图结构由若干 节点 (Vertex) 和 边 (Edge) 构成,其中:
每个节点有一个唯一 ID。
边可以是有向的(有向图,Directional Graph),也可以是无向的(无向图,Undirected Graph)。
边上可以有权重(加权图,Weighted Graph),也可以没有权重(无权图,Unweighted Graph)。
图论中的基本术语
连通性
无向图的连通性
连通图 (Connected Graph): 如果无向图中任意两个节点之间都存在一条路径,我们称这个图是连通的。
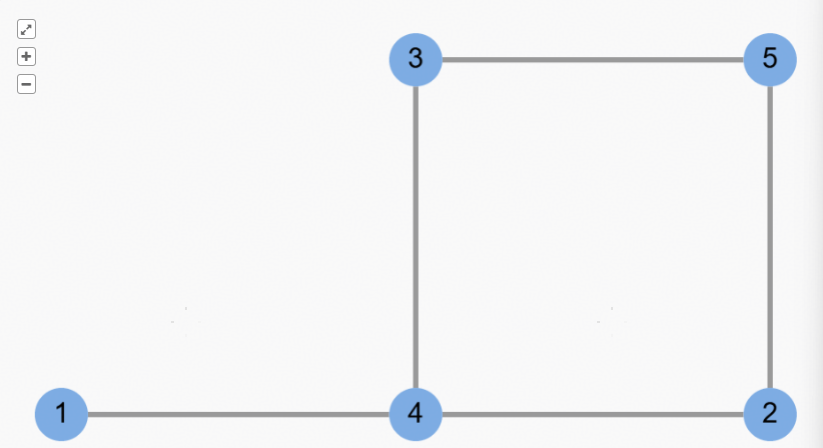
连通分量 (Connected Component):对于非连通的无向图,其中的多个连通子图被称为连通分量,一个图可以有多个连通分量。
比如下面这幅图有两个连通分量:节点 1~5 形成一个连通分量,节点 6,7 形成另一个连通分量。
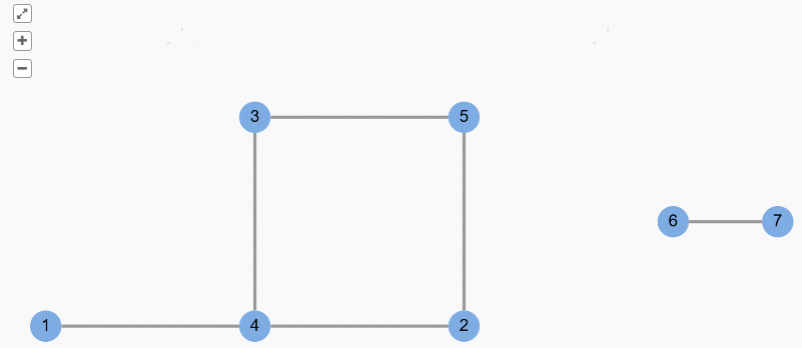
有向图的连通性
有向图的连通性概念稍微复杂一些,因为考虑到边的方向,所以有向图的连通性分为强连通和弱连通。
**强连通图 (Strongly Connected Graph):**如果有向图中任意两个节点之间都存在一条有向路径,我们称这个图是强连通的。
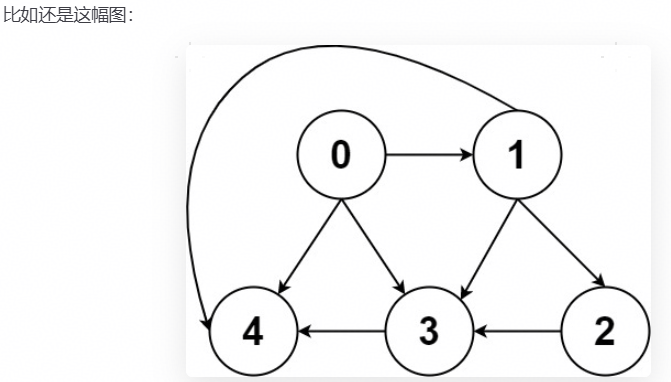
比如下面这幅图是一个强连通图,从任意节点出发都能到达其他所有节点。
**弱连通图 (Weakly Connected Graph):**如果将有向图中的所有有向边都变成无向边后,该图变成连通的,那么原来的有向图就是弱连通的。
比如下面这幅图不是强连通的(无法从节点 4 到达节点 1),但它是弱连通的,因为忽略边的方向后,所有节点之间都是连通的。
强连通分量 (Strongly Connected Component, SCC):有向图中的若干个最大的强连通子图称为强连通分量。
弱连通分量 (Weakly Connected Component, WCC):将有向图的所有有向边变为无向边后,形成的连通分量称为原有向图的弱连通分量。
图结构的通用代码实现
图结构就是 多叉树结构 的延伸。图结构逻辑上由若干节点(Vertex)和边(Edge)构成,我们一般用邻接表、邻接矩阵等方式来存储图。在树结构中,只允许父节点指向子节点,不存在子节点指向父节点的情况,子节点之间也不会互相链接;而图中没有那么多限制,节点之间可以相互指向,形成复杂的网络结构。
邻接表和邻接矩阵实现图结构
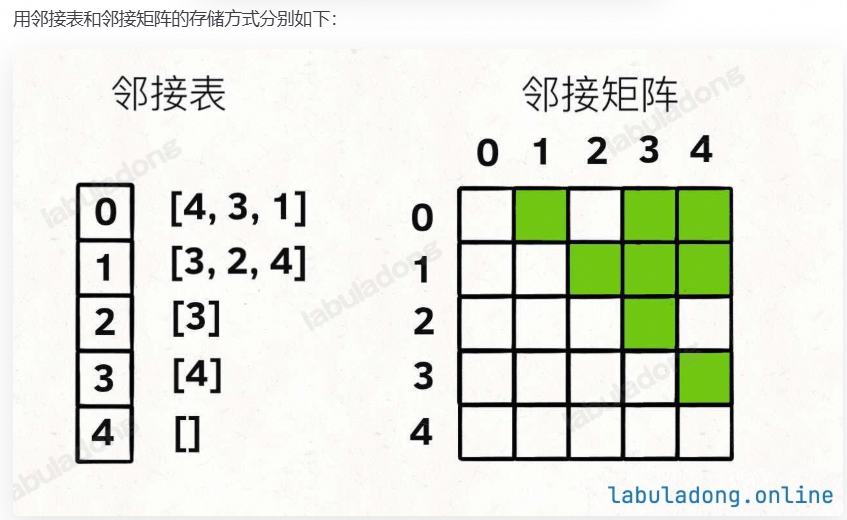
邻接表很直观,我把每个节点 x 的邻居都存到一个列表里,然后把 x 和这个列表映射起来,这样就可以通过一个节点 x 找到它的所有相邻节点。
邻接矩阵则是一个二维布尔数组,我们权且称为 matrix,如果节点 x 和 y 是相连的,那么就把 matrix[x][y] 设为 true(上图中绿色的方格代表 true)。如果想找节点 x 的邻居,去扫一圈 matrix[x][...] 就行了。