目录
前言
在上一篇文章归并排序:递归与非递归全解析中我们讲解了排序中的最后一类排序:归并排序。排序虽然分成四类但有些不属于这些类别的排序在特定场景中还是有很大的应用的。这篇文章主要讲解的是非比较排序 中的计数排序 ,虽然非比较排序中还有基数排序 和桶排序,但这两个排序在实践应用非常少见而且本身就非常复杂,所以就不进行讲解了。
计数排序
一、计数排序的概念及思路
1、计数排序的概念
计数排序 又称为鸽巢原理 ,是对哈希直接定址法 的变形应用。
2、计数排序的思路
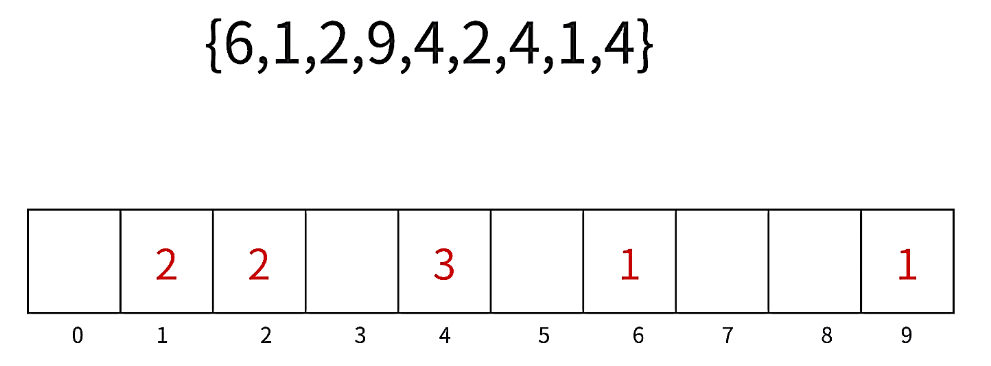
计数排序 顾名思义就是通过计算数组中每个数字出现的次数 ,就如上图所示。
其操作步骤为:
(1)找到原数组中的最大值max,利用最大值来开辟新数组
(2)统计相同元素出现次数
(3)根据统计的结果将序列回收到原来的序列中
需要注意的是:图中没有数字的地方是被初始化的0。
二、计数排序的代码实现
1、绝对映射
cpp
//Sort.h
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <time.h>
//打印数组
void PrintArray(int* arr, int n);
//计数排序
void CountSort(int* arr, int n);
//Sort.c
#include "Sort.h"
//计数排序
void CountSort(int* arr, int n)
{
//找最大值来开辟数组
int max = arr[0];
for (int i = 0; i < n; i++)
{
if (max < arr[i])
{
max = arr[i];
}
}
//计数
int range = max + 1;
int* count = (int*)calloc(range, sizeof(int));
assert(count);
//void* calloc (size_t num, size_t size);
//这里数组开辟空间不用malloc是因为我们要对数组里面所有数据初始化为0,calloc可以实现
for (int i = 0; i < n; i++)
{
count[arr[i]]++; //绝对映射
}
//排序
int j = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
arr[j++] = i; //绝对映射
}
}
}
//Test.c
#include "Sort.h"
void Test()
{
int arr[] = { 6,1,2,9,4,2,4,1,4,6 };
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
CountSort(arr, sizeof(arr) / sizeof(arr[0]));
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
int main()
{
Test();
return 0;
}
2、相对映射
但是我们想一个问题,如果此时有一个数组里面数据为{100, 101, 109, 105, 101, 105},这样的话按照上面的操作步骤我们是不是就需要创建一个大小为 sizeof(int)*110 的数组,但是我们发现最小的数都已经是100了,这就会导致一个问题:
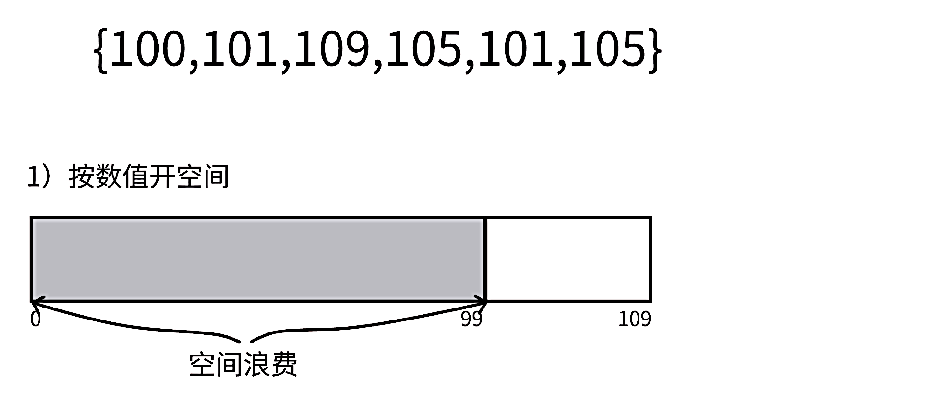
按照数组来开辟空间, 这就叫做绝对映射 。也就是说原数组中的数据 是直接与新数组的下标一一对应 的,但对于这种数组来说就会极大的浪费空间。
所以我们通过范围来开辟空间 ,则就叫做相对映射:
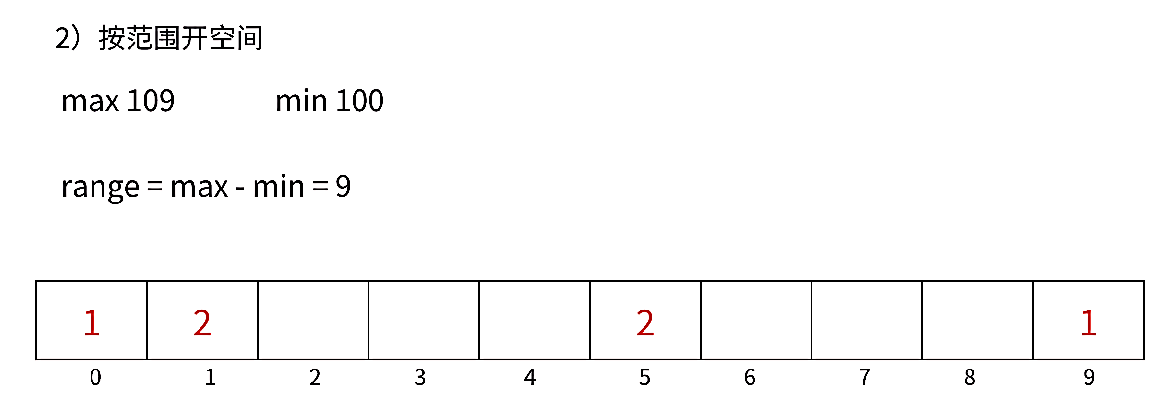
这样就可以巧妙的规避了由于最小值过大导致数组空间浪费的情况,但是当我们计数完后排序时,需要把对应下标再加上最小值 才是数组中的实际大小的值 ,也就是说此时新数组的下标并不是与原数组的数据一一对应,而是一种相对的关系。
cpp
//Sort.c
//计数排序
void CountSort(int* arr, int n)
{
//找出数组中的最大值和最小值
int min = arr[0];
int max = arr[0];
for (int i = 0; i < n; i++)
{
if (min > arr[i])
{
min = arr[i];
}
if (max < arr[i])
{
max = arr[i];
}
}
//计数
int range = max - min + 1;
int* count = (int*)calloc(range, sizeof(int));
assert(count);
//void* calloc (size_t num, size_t size);
//这里数组开辟空间不用malloc是因为我们要对数组里面所有数据初始化为0,calloc可以实现
for (int i = 0; i < n; i++)
{
count[arr[i] - min]++; //相对映射
}
//排序
int j = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
arr[j++] = i + min; //相对映射
}
}
}
//Test.c
void Test()
{
int arr[] = { 100, 101, 109, 105, 101, 105 };
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
CountSort(arr, sizeof(arr) / sizeof(arr[0]));
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
int main()
{
Test();
return 0;
}
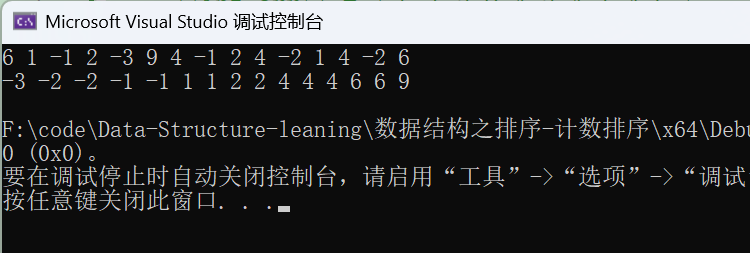
并且由于是相对的关系 ,相对映射的代码是可以实现数组中有负数情况的排序 的,但是对于绝对映射 来说这就是不可行 的,因为没有数组下标为负数的情况。
cpp
//Test.c
void Test()
{
int arr[] = { 6,1,-1,2,-3,9,4,-1,2,4,-2,1,4,-2,6 };
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
CountSort(arr, sizeof(arr) / sizeof(arr[0]));
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
int main()
{
Test();
return 0;
}
三、计数排序的复杂度
1、时间复杂度
由上面的代码我们就能知道计数排序的循环次数为 :2N + count*range ,所以计数排序的时间复杂度为:O(N + range)
2、空间复杂度
由于计数排序需要开辟空间大小为sizeof(int)*range 的数组,所以计数排序的空间复杂度为:O(range)
四、计数排序的优缺点
计数排序的优势区间:
(1)由于上面我们说到了计数排序的时间复杂度 为O(N + range) ,这个复杂度的大小其实是远比我们之前所学的所有排序都要小的,这就使得这个排序在特定场景的排序效果是非常好 的。我们可以利用之前一篇文章深入解析插入排序与希尔排序所讲的检测排序效率的代码观察一下计数排序的效率有多高:
cpp
//Test.c
#include <time.h>
void Test2()
{
srand(time(0));
const int N = 10000000;
int* a1 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand() + i;
}
int begin1 = clock();
CountSort(a1, N);
int end1 = clock();
printf("CountSort:%d\n", end1 - begin1);
free(a1);
a1 = NULL;
}
int main()
{
Test2();
return 0;
}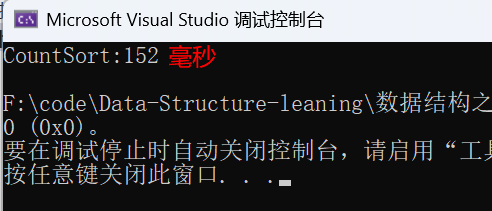
我们会发现在数据量为一千万的情况下计数排序所消耗的时间都只有一百多毫秒,而在前面不管是希尔排序还是快速排序,在这个数据量的情况下所消耗的时间都是接近一秒的,这就足以见得计数排序的效率之高。
计数排序的劣势区间:
(1)如果计数排序真的像上面那样效率高,为什么没有像希尔排序或者快速排序那样常用呢?这就需要说到它的劣势:首先是计数排序只能对整数进行排序 。这个劣势其实就会导致计数排序的使用场景非常有限。
(2)其次是只有数据范围集中的情况计数排序效率才高 ,当数据非常分散的时候比如:{ -1, 100, 101, 109, 105, 101, 105},这就会导致开辟的数组空间非常大但数据量少 的情况,也就和上面所讲的绝对映射一样导致大量空间浪费的问题。
排序算法复杂度及稳定性分析
稳定性: 假定在待排序的记录序列中,存在多个 具有相同的关键字 的记录。若经过排序,这些记录的相对次序保持不变 ,即在原序列 中,r[ i ] = r[ j ],且 r[ i ] 在 r[ j ] 之前,而在排序后 的序列中,r[ i ] 仍在 r[ j ] 之前,则称这种排序算法 是稳定的;否则称为不稳定的。
当我们把这几个排序讲解完后可以把算法复杂度 进行一次小结,并且对这些排序的稳定性进行分析:
|----------------------------------------------------------------------------------------------------------|------------|-------------|---------|
| 排序方法 | 时间复杂度 | 空间复杂度 | 稳定性 |
| 直接插入排序 | O(N^2) | O(1) | 稳定 |
| 希尔排序 | O(N^1.3) | O(1) | 不稳定 |
| 直接选择排序 | O(N^2) | O(1) | 不稳定 |
| 堆排序 | O(N*logN) | O(1) | 不稳定 |
| 冒泡排序 | O(N^2) | O(1) | 稳定 |
| 快速排序 | O(N*logN) | O(logN) | 不稳定 |
| 归并排序 | O(N*logN) | O(N) | 稳定 |
这里着重讲解一下黑体字的部分,其他的再对应排序的讲解中已经涉及到了,这里就不过多赘述了。
首先是快速排序 的空间复杂度为什么为:O(logN) 这里我们要先清楚递归在栈区开辟空间时的一个要点:当递归返回时,下一个递归所需栈空间是可以利用上一个递归所开辟的栈空间,也就是说递归开辟的栈空间是可以重复利用的 。
而我们在学习快排 时知道这个排序是类似二叉树的前序遍历 ,递归的深度为:logN 。而每一层的递归 就是共用同一个栈空间 ,所以快排额外开辟的栈空间数量为 logN ,也就是说快排的空间复杂度为:O(logN)
再说一下归并排序 的空间复杂度为什么为:O(N) 由于归并排序不同于这些排序,需要借助额外开辟的第三方数组进行存值 ,所以单是开辟新数组归并排序的空间复杂度就已经是O(N)。 又因为归并排序类似二叉树的后序遍历 ,其实就和快速排序一样需要额外开辟栈空间的数量为 logN ,但是 N 的阶级是高于 logN 的,空间复杂度 是可以忽略logN ,所以归并排序的空间复杂度为:O(N)
最后讲一下直接选择排序 为什么是不稳定 的:
按照直接选择排序的逻辑我们会想当然以为是稳定的,因为每次我们是选出最小的数与前面的数进行交换,如果几个数相同我们也只会选第一个数进行交换,这样感觉不会影响相同数之间的顺序,但之所以要拿出来单独讲解就是因为有些特例:比如一个数组{6, 6, 1}
当我们第一次遍历数组找最小值则是1,这样1就要和数组开头的6进行交换,此时就会出现相同数顺序改变的情况:{1, 6, 6}。其实跨越进行交换 都可能出现不稳定的情况。
结束语
到此我们的初阶数据结构就彻底完结了,下一篇文章我们就会正式步入C++语言的学习,感谢大家一路的支持,在C++中我会更加细致讲解知识点。不管是学习还是复习知识点的朋友,就是为了更好让大家看得懂,听得明白。希望我的文章能对大家学习数据结构有所帮助!