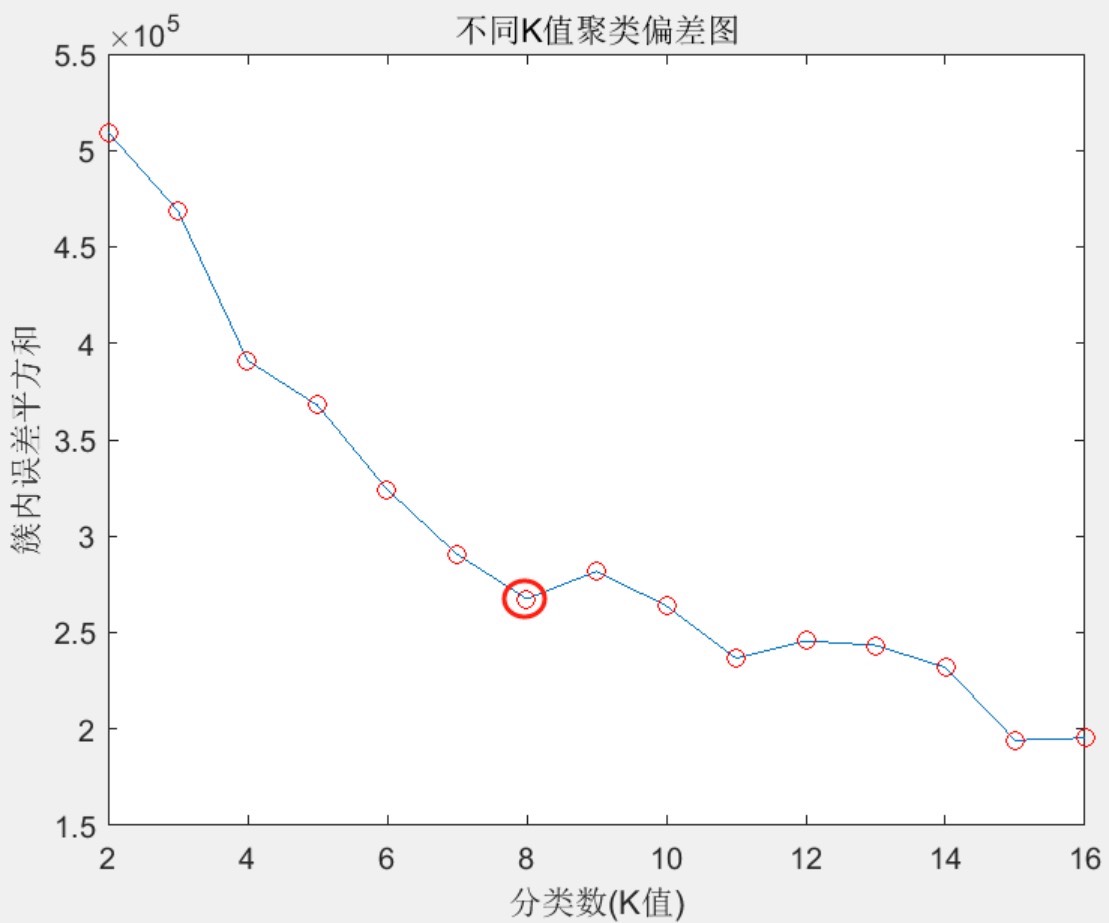
基于手肘法的kmeans聚类数的精确识别matlab 1.程序内置风电功率和光伏发电功率的拉丁超立方抽样算法,形成了数据集。 2.明确了数据更改方式,增加了详尽的修改方法注释,方便上手改成自己的数据。 3.可以得到不同聚类场景的概率以及聚类中心数据,程序注释清楚,方便研究使用。 4.采用两种方式进行分析,第一种是全年365天实测风力数据,第二种是拉丁超立方抽样方式。
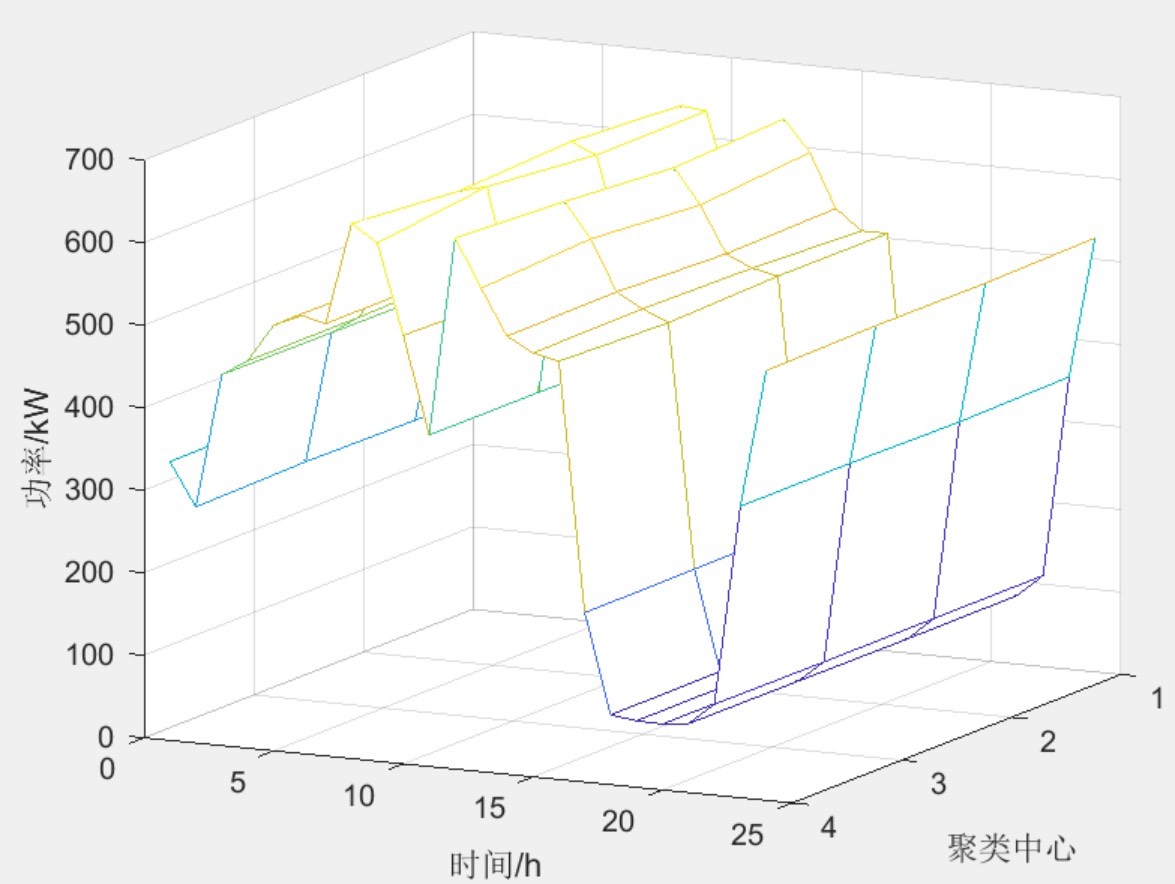
在能源领域的数据分析中,准确识别聚类数对于理解风电功率和光伏发电功率的数据模式至关重要。今天咱们就来唠唠基于手肘法的kmeans聚类数在Matlab里是怎么实现精确识别的,还会涉及风电和光伏功率相关数据处理。
数据生成:拉丁超立方抽样算法
程序里内置了风电功率和光伏发电功率的拉丁超立方抽样算法,以此来形成数据集。这算法有啥好呢?它能在给定的参数范围内,更均匀地抽取样本点,比传统随机抽样得到的样本更能代表总体分布。
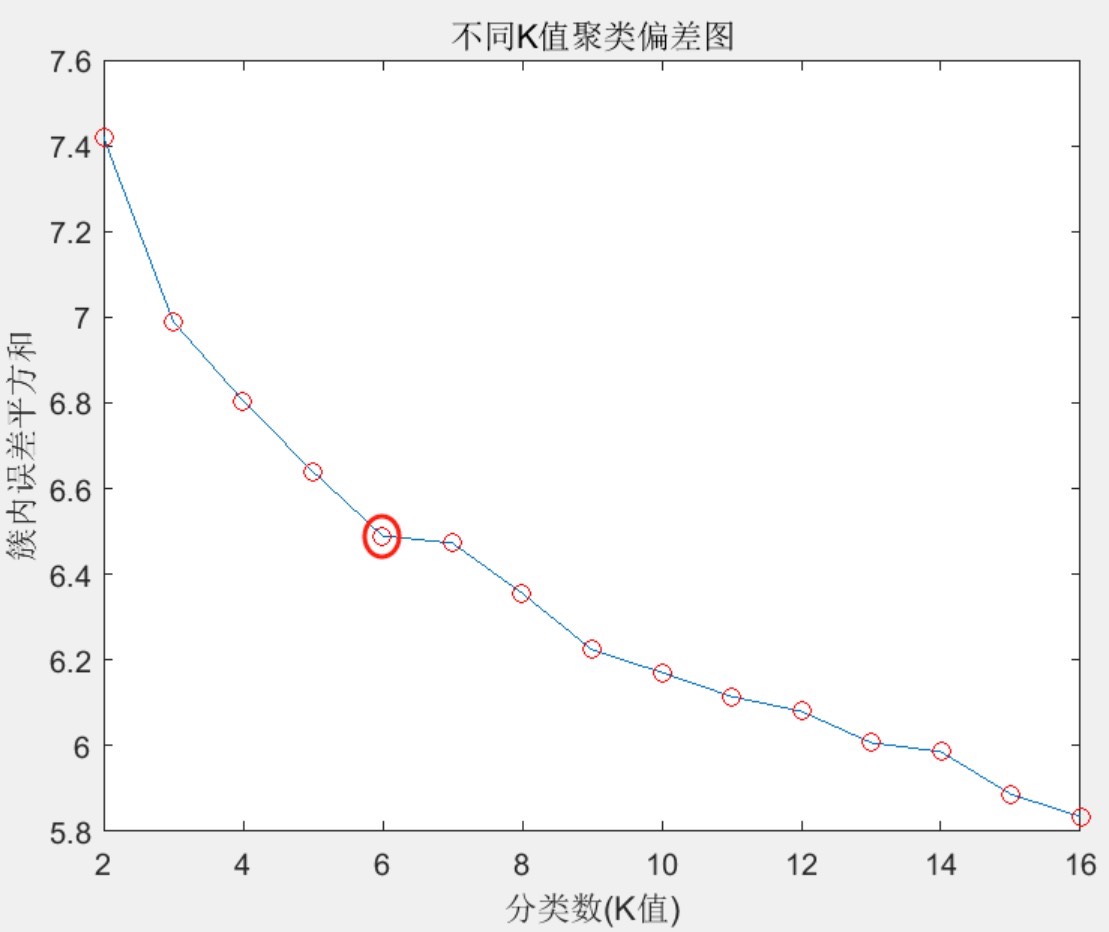
下面是一个简单示意的拉丁超立方抽样代码(这里只是示意关键部分,并非完整可运行代码):
matlab
% 假设我们要生成风电功率数据的拉丁超立方样本
n = 100; % 样本数量
min_power = 0; % 风电功率最小值
max_power = 1000; % 风电功率最大值
% 生成拉丁超立方样本
lhs_sample = lhsdesign(n,1,'criterion','center');
wind_power = min_power + (max_power - min_power) * lhs_sample;这里,lhsdesign函数生成了拉丁超立方抽样的样本结构,然后通过线性变换将样本映射到我们设定的风电功率范围 [minpower, maxpower] 内。
数据更改与注释
明确了数据更改方式,而且增加了详尽的修改方法注释,这对于咱们想要改成自己的数据来说,可太友好了。比如说,如果你的实际风电功率数据范围跟代码里预设的不一样,按照注释里说的,改改 minpower**和 max power 这俩参数就行。
matlab
% 如果你自己的数据风电功率范围是50 - 800
% 就把这两行改一下
min_power = 50;
max_power = 800; 这样简单一改,就能适配你的实际数据范围了。
分析方式与结果
两种分析方式
咱们采用了两种方式进行分析。第一种是全年365天实测风力数据,直接拿实际测量的数据来分析,这能最真实地反映风力发电的实际情况。第二种是拉丁超立方抽样方式,前面也提到过它能均匀抽样形成数据集。
可获得的结果
通过程序,我们可以得到不同聚类场景的概率以及聚类中心数据。程序注释清楚,对于研究来说可太方便了。比如说,在计算聚类中心数据的时候,代码是这么写的(同样为示意关键部分):
matlab
% 使用kmeans算法进行聚类
k = 3; % 假设聚类数为3
[idx,C] = kmeans(wind_power,k);
% idx是每个数据点所属的聚类索引
% C就是聚类中心数据这里通过 kmeans 函数,将风电功率数据按照设定的聚类数 k 进行聚类,返回的数据 idx 能让我们知道每个数据点属于哪个聚类,而 C 就是各个聚类的中心数据。通过分析这些聚类中心数据,我们能了解不同模式下的风电功率特征。而不同聚类场景的概率,也能帮助我们评估每种聚类模式在整体数据中的占比情况,为进一步研究风电功率的分布规律提供依据。
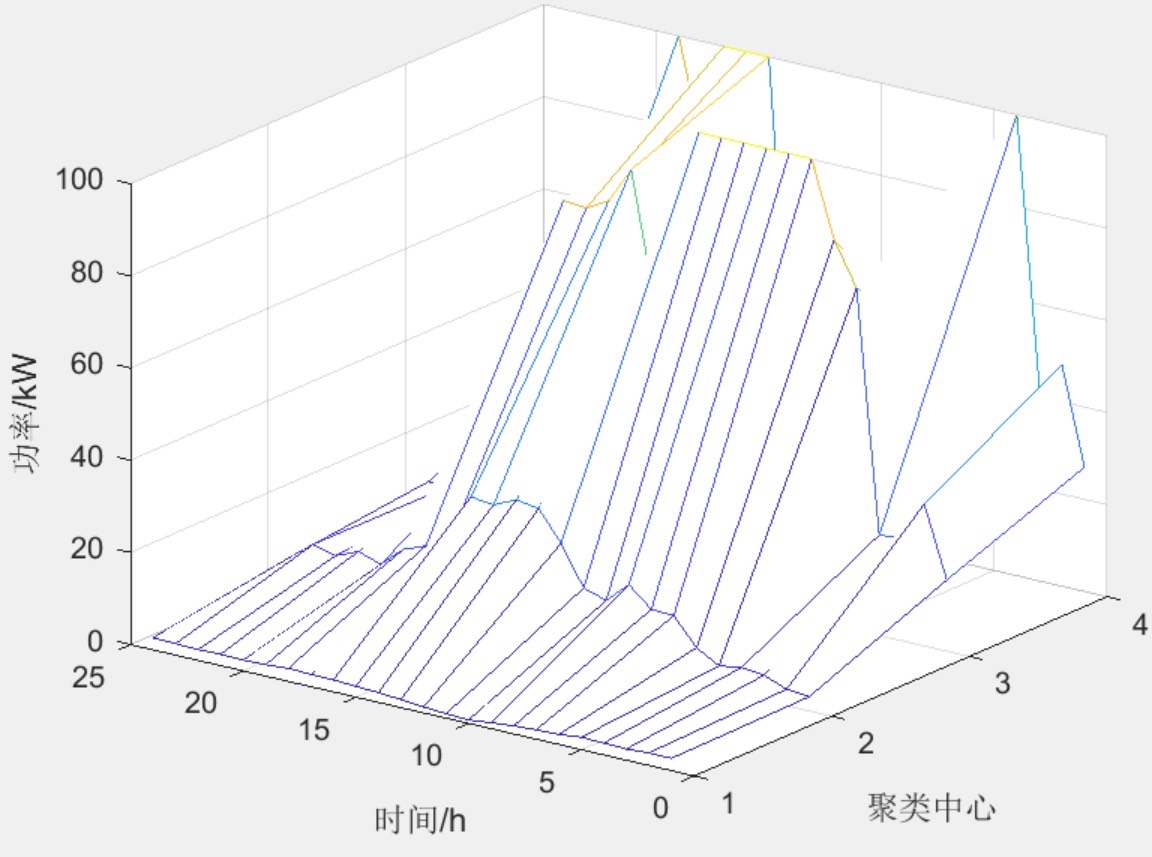
总之,基于手肘法的kmeans聚类数精确识别在Matlab中的这个程序,无论是数据生成、数据更改,还是分析方式和结果呈现,都设计得很贴心,为风电和光伏发电功率的研究提供了有力的工具。