可以看穿事物“本质“的LDA

前言

假设你是一个机器人开发者，某天你倒了两杯饮料一杯绿茶一杯可乐。这时候你要教你的机器人如何快速的品尝出哪一杯是绿茶，哪一杯是可乐。

你该怎么做呢？

也许你会求教你的好朋友饮料专家A，A会列举一大堆数据告诉机器人。比如可乐的含糖量是多少、绿茶中的含糖量多少，咖啡因、香精等等各种含量。这时候你的机器人可能已经开始冒烟死机了，为什么呢？参数太多了它记不住。
这时候你的吃货朋友B在旁边笑着说：你们干嘛这么折磨它，直接告诉它可乐有气泡，绿茶没有气泡不就好了吗？结果呢，机器人直接就指出了正确的答案。

在这里，"有气泡"和"无气泡"就是二者区分的最好特征，那么对于为什么"含咖啡因量"、"甜度"这些不是好的特征呢？

在机器学习中，我们经常也会面临这些问题，我们有高维的数据，但是呢数据又很稀疏，不仅计算复杂度高，往往还会过拟合。找到重要特征，对数据进行降维就成了数据预处理中的关键一步。这时候就需要我们今天的主角LDA出场了。

什么是LDA

LDA（Linear Discriminant Analysis, 线性判别分析） 是一种经典的有监督的降维和分类方法。由统计学家Ronald A. Fisher 于 1936 年提出，一开始用于解决二分类问题，也叫Fisher判别分析。其核心目标是：在降低数据维度的同时，可以最大化类间距离，最小化类内距离。

最大化类间距离：就是让不同类别的事物离中心越远越好，比如可乐和绿茶在有无气泡上就划分的很明显。
最小化类内距离 ：同一类别的事物在某个特征投影上，或者说在某个指标上，大家的位置相对集中，比如可乐和可乐，二者的咖啡因含量相差很少。

LDA的目标，就是找到一条直线，使得二者的比值达到最大。也就是max(类间距离/类内距离）.这个值越大，说明不同类之间分的越大，同类之间靠得越近，效果也最好。

LDA数学模型

虽然很多人（包括我）一看到数学就头疼，但LDA逻辑很简单，我们只看最关键的几步。

数学符号定义

假设我们有NNN个样本，这些样本一共被分为CCC个类别。那么

第iii类的样本集合为Xi\mathcal{X}_iXi, 大小为 NiN_iNi，则∑i=1CNi=N\sum{i=1}^C N_i = N∑i=1CNi=N
第iii 类的样本均值为：μi=1Ni∑x∈Xix{\mu_i} = \frac{1}{N_i} \sum_{\mathbf{x} \in \mathcal{X}_i} \mathbf{x}μi=Ni1∑x∈Xix
全局的均值为：μ=1N∑i=1C∑x∈Xix=1N∑i=1CNiμi{\mu} = \frac{1}{N} \sum_{i=1}^C \sum_{\mathbf{x} \in \mathcal{X}i} \mathbf{x} = \frac{1}{N} \sum_{i=1}^C N_i{\mu}_iμ=N1∑i=1C∑x∈Xix=N1∑i=1CNiμi
设投影方向单位向量 w∈Rd\mathbf{w} \in \mathbb{R}^dw∈Rd，任一样本x\mathbf{x}x投影后的标量为 y=w⊤xy=\mathbf{w}^⊤\mathbf{x}y=w⊤x

类内散度

类内散度，也就是我们上面说的类内距离，它衡量的是：每个样本离自己所属类别的中心有多远，然后相加求和。

第iii类的类内方差为: σi2=∑x∈Xi(w⊤x−w⊤μi)2=w⊤(∑x∈Xi(x−μi)(x−μi)⊤)w\sigma_i^2 = \sum_{\mathbf{x} \in \mathcal{X}i} (\mathbf{w}^\top \mathbf{x} - \mathbf{w}^\top{\mu}i)^2 = \mathbf{w}^\top \left( \sum{\mathbf{x} \in \mathcal{X}_i} (\mathbf{x} - {\mu}_i)(\mathbf{x} - {\mu}_i)^\top \right) \mathbf{w}σi2=∑x∈Xi(w⊤x−w⊤μi)2=w⊤(∑x∈Xi(x−μi)(x−μi)⊤)w
定义第iii类的类内散度矩阵为: Si=∑x∈Xi(x−μi)(x−μi)⊤S_i = \sum_{\mathbf{x} \in \mathcal{X}_i} (\mathbf{x} - {\mu}_i)(\mathbf{x} -{\mu}_i)^\topSi=∑x∈Xi(x−μi)(x−μi)⊤
则总的类内散度是: SW=∑i=1CSi=∑i=1C∑x∈Xi(x−μi)(x−μi)⊤S_W = \sum_{i=1}^C S_i = \sum_{i=1}^C \sum_{\mathbf{x} \in \mathcal{X}_i} (\mathbf{x} - {\mu}_i)(\mathbf{x} - {\mu}_i)^\topSW=∑i=1CSi=∑i=1C∑x∈Xi(x−μi)(x−μi)⊤
投影后的总类内散度为: JW=w⊤SWwJ_W = \mathbf{w}^\top S_W \mathbf{w}JW=w⊤SWw。

类间散度

类间散度，即上述的类间距离。衡量的是各类中心在投影中的分离程度。

第iii类中心投影为: w⊤μi\mathbf{w}^\top{\mu}_iw⊤μi
全局均值投影为: w⊤μ\mathbf{w}^\top{\mu}w⊤μ
类间散度定义为:JB=∑i=1CNi(w⊤μi−w⊤μ)2=w⊤(∑i=1CNi(μi−μ)(μi−μ)⊤)wJ_B = \sum_{i=1}^C N_i (\mathbf{w}^\top{\mu}i - \mathbf{w}^\top{\mu})^2 = \mathbf{w}^\top \left( \sum_{i=1}^C N_i ({\mu}_i - {\mu})({\mu}_i - {\mu})^\top \right) \mathbf{w}JB=∑i=1CNi(w⊤μi−w⊤μ)2=w⊤(∑i=1CNi(μi−μ)(μi−μ)⊤)w
因此，类间散度矩阵为: SB=∑i=1CNi(μi−μ)(μi−μ)⊤S_B = \sum_{i=1}^C N_i ({\mu}_i - {\mu})({\mu}_i - {\mu})^\topSB=∑i=1CNi(μi−μ)(μi−μ)⊤
投影后的类间散度为: JB=w⊤SBwJ_B = \mathbf{w}^\top S_B \mathbf{w}JB=w⊤SBw

优化目标

LDA 寻找投影方向 w\mathbf{w}w使得
max⁡wJBJW=w⊤SBww⊤SWw\max_{\mathbf{w}} \frac{J_B}{J_W} = \frac{\mathbf{w}^\top S_B \mathbf{w}}{\mathbf{w}^\top S_W \mathbf{w}}maxwJWJB=w⊤SWww⊤SBw

这个比值越大越好。

单维解（一维LDA)

对上述优化目标中的比值求导并令梯度等于零，可得最优解w\mathbf{w}w满足： SBw=λSWwS_B \mathbf{w} = \lambda S_W \mathbf{w}SBw=λSWw

即可求解广义特征值问题（前提SWS_WSW可逆）
SW−1SBw=λwS_W^{-1} S_B \mathbf{w} = \lambda \mathbf{w}SW−1SBw=λw

最大值对应的最大特征值λmax⁡\lambda_{\max}λmax，对应的特征向量即为最优投影方向w∗\mathbf{w}^*w∗。

多维解（多类LDA)

有CCC个类别时，最多可获得C−1C-1C−1个有效判别方向。这是因为SBS_BSB的秩最多为C−1C - 1C−1，因为所有类中心相对于全局均值只有C−1C - 1C−1个独立方向。

求解广义特征值问题: SBW=SWWΛS_B \mathbf{W} = S_W \mathbf{W} \mathbf{\Lambda}SBW=SWWΛ或SW−1SBW=WΛS_W^{-1} S_B \mathbf{W} = \mathbf{W}\mathbf{\Lambda}SW−1SBW=WΛ 其中

W=[w1,w2,...,wC−1]∈Rd×(C−1)\mathbf{W} = [\mathbf{w}_1, \mathbf{w}2, \dots, \mathbf{w}{C-1}] \in \mathbb{R}^{d \times (C-1)}W=[w1,w2,...,wC−1]∈Rd×(C−1)
Λ\mathbf{\Lambda}Λ为对角矩阵，包含前C−1C-1C−1个最大特征值

最终，将原始数据X∈RN×d\mathbf{X} \in \mathbb{R}^{N \times d}X∈RN×d投影到低维空间: Y=XW∈RN×(C−1)\mathbf{Y} = \mathbf{X} \mathbf{W} \in \mathbb{R}^{N \times (C-1)}Y=XW∈RN×(C−1)，该子空间能最大程度保留类别可分性。

LDA算法步骤

计算每个类别的均值μi{\mu}_iμi和全局均值μ{\mu}μ；
计算类内散度矩阵SW\mathbf{S}_WSW；
计算类间散度矩阵SB\mathbf{S}_BSB；
求解广义特征值问题SW−1SBw=λw\mathbf{S}_W^{-1} \mathbf{S}_B \mathbf{w} = \lambda \mathbf{w}SW−1SBw=λw
选取前kkk个最大特征值对应的特征向量，构成投影矩阵W\mathbf{W}W；
对原始数据进行投影Xnew=XW\mathbf{X}_{\text{new}} = \mathbf{X} \mathbf{W}Xnew=XW。

LDA局限性

对数据有要求：它需要"规规矩矩"的数据，假设每个类别的数据都服从高斯分布，并且假设所有类别的协方差矩阵也是相同的。
线性边界：它是线性分类器，只能处理线性可分的问题，对于螺旋形、环形分布的数据就不行了。
需要标签：有监督类算法，需要标签数据。
对异常值敏感。

Python代码实现

我们使用sklearn中的经典鸢尾花数据集为例，它有4个特征，3个类别。

加载库与数据

python 复制代码

from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

iris = datasets.load_iris()
data_x = iris.data
data_y = iris.target

使用LDA降至2维

python 复制代码

lda = LinearDiscriminantAnalysis(n_components=2)
lda_data_x = lda.fit_transform(data_x, data_y)

画图

python 复制代码

plt.figure(figsize=(8, 6))
colors = ['red', 'green', 'blue']
for i, color, name in zip([0, 1, 2], colors, iris.target_names):
    plt.scatter(
      lda_data_x[y == i, 0], 
      lda_data_x[y == i, 1],
      c=color, label=name, alpha=0.8
      )

plt.xlabel('判别方向 1 (LD1)')
plt.ylabel('判别方向 2 (LD2)')
plt.title('LDA 降维后的鸢尾花数据')
plt.legend()
plt.grid(True)
plt.show()

结果如下：

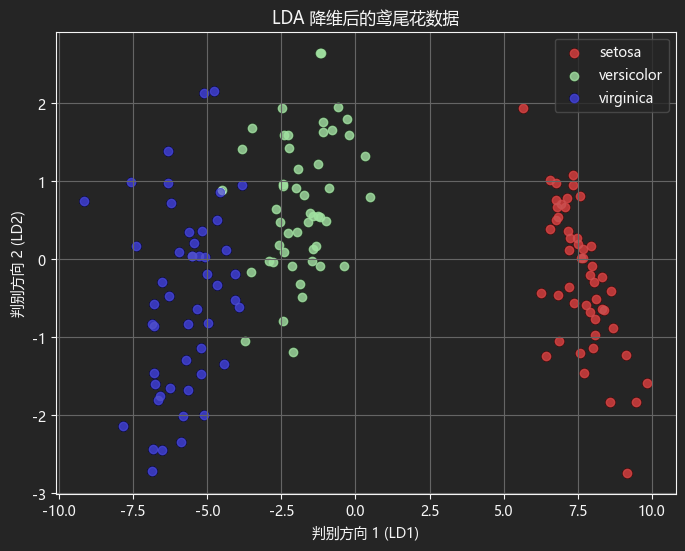
从图中可以看出，这三种类别的数据在判别方向1上几乎完全分开，特别是红色的setosa数据，说明 LDA 成功找到了最佳判别方向。

结语

关于LDA, 我们已经从原理、数学、代码全方位地聊了一遍，最后我们总结一下：

LDA是连接统计学与机器学习的经典桥梁，但它又不仅仅是一个算法，更是一种思维方式 ，它告诉我们在面对一个复杂问题时，不要迷失在海量的信息和特征中，要学会抓住主要矛盾，找到那个最能区分问题本质的"黄金视角"。尽管现代深度学习已能自动学习判别性特征，但 LDA 因其简洁、可解释、高效的特点，仍在许多领域发挥着不可替代的作用。

掌握LDA，不仅是学习一个算法，更是理解有监督表示学习的起点。