前言
贝塞尔曲线是个老生常谈的话题了,尤其是三阶贝塞尔算是用的最广泛、说的最烂的一个了。但是理论归理论,都说得天花乱坠,至今却没有一个能真正解决问题的方案。本次就"根据指定数量的数据点,如何画出一个完美的贝塞尔"的问题做个了解吧。
什么是贝塞尔
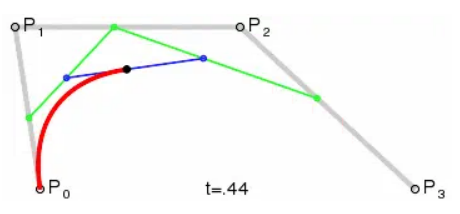
至于这个问题不再做重复解释,放个图镇镇楼。
实战需求
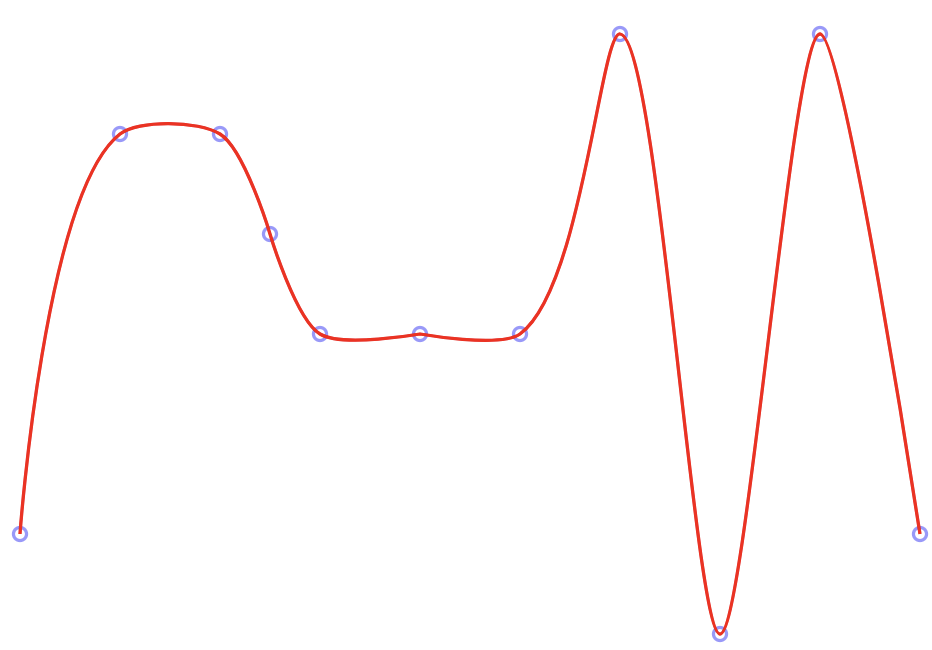
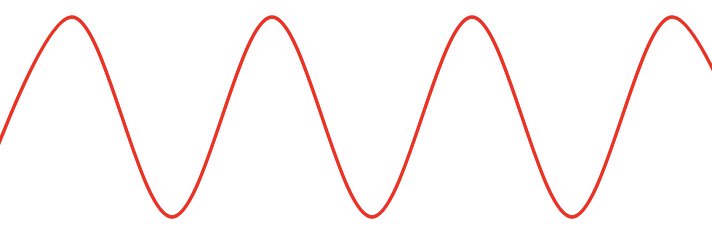
已知有n个根据x排序好的List<Point>数据,用曲线将它们平滑的连起来,并且每个点都是曲线的顶点或者曲线经过的点。如下,ui设计2分钟就搞好的效果图:
现状
看着这个图,第一个感觉自然是有手就行,xx搜一下,嘿嘿网上还挺多。
第一个版本(二阶贝塞尔):
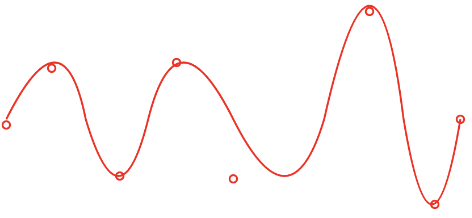
虽然有波形效果,但顶点大部分都对不上......
第二个版本(三阶贝塞尔1):
 (偷懒版)
(偷懒版)
大部分刚从网上得到的和二阶的问题一样,都是顶点很难对得上的问题
第三个版本(三阶贝塞尔2):
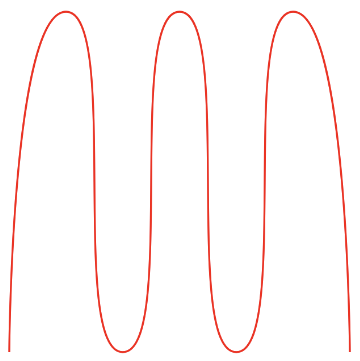
有些方案为了对上顶点,每个画的都很圆润,这样容错就更高了,但很明显太丑了。
第n个版本:
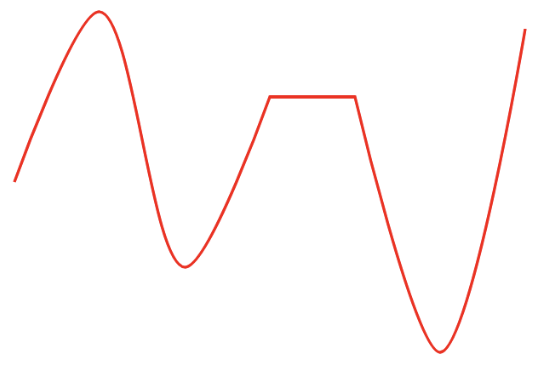
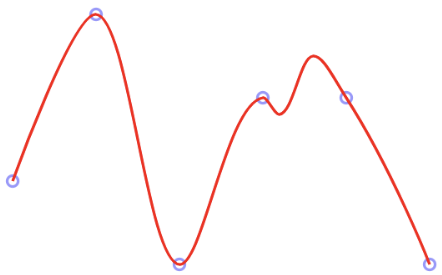
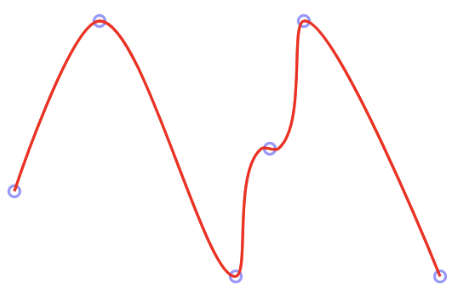
用了n个版本后发现,大部分普通数据还是能对上的,但是一遇到几个点共线、差距过大或者非常接近的情况总会出现各种意想不到的结果。
反思
**关于二阶贝塞尔:**由于起点和终点都是比较平的曲线,所以当顶点的只能是控制点画出的那个位置,然而它的终点选的不对会导致下一个贝塞尔很难圆回去,下一个又会影响下下一个,并且根据起点、终点和顶点目前没有什么好的公式来推导出控制点(目前只推出控制点一定在三个点的角平分线上),所以要想画一个完全符合要求的线基本上不太可能(如果有数学大神做出来记得@我膜拜一下)。
**关于三阶贝塞尔:**上面几个贝塞尔查看代码可以发现,基本上都是没有任何关联的凑数,一遇见特殊情况就很难解决。
归纳
首先,要想画出的线顶点对齐到坐标上,那终点肯定得是顶点(参考二阶贝塞尔的问题,很难通过通用公式来得到贝塞尔里面的顶点),也就是说我们得一半一半的画。
然后就是问题了:控制点该怎么找?下一段该怎么画?
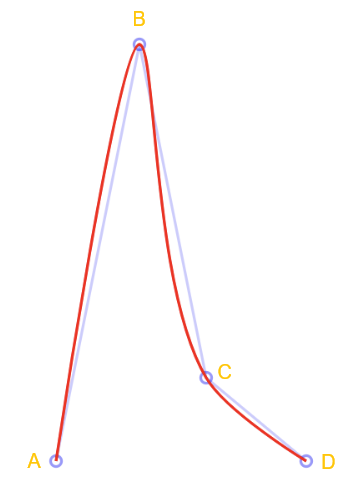
如下图,4个点画的贝塞尔曲线,对于点B和C,为什么B比C尖? 这个很好判断,因为∠ABC比∠BCD小。那又有问题了,**画贝塞尔时如何控制尖的程度呢?**我们先随便画几个不同弧度大小的控制点:
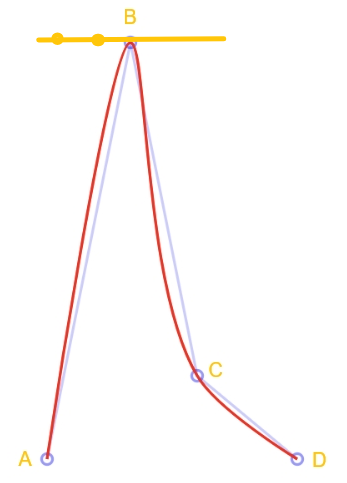
很明显,同一条线下控制点的远近决定了角度大小,这样我们就得到"同一直线下角度越小控制点越近 "。那这条线又该取条呢?
根据上面的示意图,基本上都应该有个底了"B的切线就是控制点所在的线 ",但是B的切线如何得到?
这......
反正博主是算不出来
但是......
还是老话:"我们又不是数学家,我们不是来解数学题的 ",我们只需要找到一个近似切线的线不就行了。在∠ABC中,有哪根线能很容易得到一个近似的切线?
那就是当之无愧的"角平分线 "了,因为角平分线的垂直线无论在什么情况下都近似等于B的切线。
切线找到了,控制点的范围也锁定了,但直线毕竟是无穷长的,该选哪个点为控制点呢?
这个应该很容易想到,无论图大小长短,都和AB、BC长度有关,那默认控制点就以AB长度为最大值,当然由于AB可能很长,以A点到控制线的垂直点为基础控制点的最大值更好。
至此我们就完整归纳出一个适配所有场景的画贝塞尔曲线的方式:以∠ABC的角平分线的垂直线为控制点所在直线,点A到直线的点为控制点基本最大点,根据∠ABC的大小占180°的百分比来确定控制点坐标。
代码
思路有了,代码自然是少不了,当然实际的代码也做了一些边界的处理。至于iOS、Web、PC端也可自行参考,现在ai也方便,其他端自行翻译吧。
Kotlin
object BezierUtil {
/**
* 使用静态缓存来减少大量的内部对象
*/
private val temp1 = PointF(0f, 0f)
private val temp2 = PointF(0f, 0f)
private val tempControl1 = PointF(0f, 0f)
private val tempControl2 = PointF(0f, 0f)
/**
* 根据[points]画贝塞尔曲线
* @param points 坐标点,请自行排序好
* @param isClosed 曲线是否需要闭合(贝塞尔方式闭合)
* @param radianCoefficient 每个点弧度的系数,值越大弧度圆润,值越小弧度越尖,建议0-1
* 示例:1f每个顶点弧度都很圆润(正六边形可以画出个正圆),0f画出来的就是直连没有弧度
* 注意:过大可能会出现轻微偏差导致看上去有多个顶点,超出1可能无法正确算出来
* @param reset 是否清除path,true:rest并重新开始;false:不重置接着使用lintTo(接力方式)
*/
@MainThread
fun createBezierPathThroughPoints(points: List<PointF>, path: Path, isClosed: Boolean, radianCoefficient: Float = 0.8f, reset: Boolean = true) {
/**
* 内角角度(180(π)度的比例)
*/
fun calculateAngleRatio(a: PointF, b: PointF, c: PointF): Float {
if (a == b || a == c || b == c) return 1f
// 创建向量
val ba = temp1.apply { set(a.x - b.x, a.y - b.y) }
val bc = temp2.apply { set(c.x - b.x, c.y - b.y) }
// 根据点积和向量模长计算余弦值(避免除零错误),并限制余弦值范围(防止浮点数误差导致反余弦异常)
val clampedCos = ((ba.x * bc.x + ba.y * bc.y) / (ba.length() * bc.length())).coerceIn(-1.0f, 1.0f)
return acos(clampedCos) / PI.toFloat()
}
fun getControl1(lastC: PointF, p: PointF, p1: PointF, ratio: Float): PointF {
// 计算向量lastC/p
val vectorAB = temp1.apply { set(p.x - lastC.x, p.y - lastC.y) }
val distAB = vectorAB.length()
// p/p1重合
if (distAB == 0f) return p
// 计算p/p1的距离
val bc = temp2.apply { set(p1.x - p.x, p1.y - p.y) }.length() * ratio
// lastC/p方向的单位向量计算坐标
return tempControl1.apply { set(p.x + vectorAB.x / distAB * bc, p.y + vectorAB.y / distAB * bc) }
}
fun getControl2(p: PointF, p1: PointF, p2: PointF, ratio: Float): PointF {
if (p == p1 || p == p2 || p1 == p2) return p1//重合就返回默认
// 计算向量
val ba = temp1.apply { set(p.x - p1.x, p.y - p1.y) }
val lenBA = ba.length()
val bc = temp2.apply { set(p2.x - p1.x, p2.y - p1.y) }
val lenBC = bc.length()
// 根据单位向量计算角平分线方向向量
val bisectorX = ba.x / lenBA + bc.x / lenBC
val bisectorY = ba.y / lenBA + bc.y / lenBC
if (bisectorX == 0f && bisectorY == 0f) return p1// 180度角
// 计算角平分线的垂直向量并归一化
val perp = temp2.apply {
x = -bisectorY// 逆时针旋转90度
y = bisectorX
}
if (perp.x == 0f && perp.y == 0f) return p1
val lenPerp = perp.length()
val perpUnit = temp2.apply { set(perp.x / lenPerp, perp.y / lenPerp) }
// 根据点积符号确定t的方向
val t = if (ba.x * perpUnit.x + ba.y * perpUnit.y > 0) ratio * lenBA else -ratio * lenBA
return tempControl2.apply { set(p1.x + t * perpUnit.x, p1.y + t * perpUnit.y) }
}
fun moveOrLine(x: Float, y: Float) = if (reset) path.moveTo(x, y) else path.lineTo(x, y)
if (reset) {
path.reset()
}
when (points.size) {
0 -> return
1 -> return moveOrLine(points[0].x, points[0].y)
2 -> return moveOrLine(points[0].x, points[0].y).also { path.lineTo(points[1].x, points[1].y) }
}
moveOrLine(points[0].x, points[0].y)
val rc = radianCoefficient.coerceIn(0f, 20f) * 0.5f
if (isClosed) {
var preRatio = calculateAngleRatio(points[points.lastIndex], points[0], points[1])
var preC2 = getControl2(points[points.lastIndex], points[0], points[1], preRatio * rc)
points.forEachIndexed { index, p ->
val p1 = points[(index + 1) % points.size]
val p2 = points[(index + 2) % points.size]
val angleRatio = calculateAngleRatio(p, p1, p2)
val control1 = getControl1(preC2, p, p1, preRatio * rc)
val control2 = getControl2(p, p1, p2, angleRatio * rc)
preC2 = control2
preRatio = angleRatio
path.cubicTo(control1.x, control1.y, control2.x, control2.y, p1.x, p1.y)
}
path.close()
} else {
var preRatio = 1f
var preC2 = points.first()
for (index in 0 until points.lastIndex) {
val p = points[index]
val p1 = points[index + 1]
val p2 = points.getOrNull(index + 2) ?: p1
val angleRatio = calculateAngleRatio(p, p1, p2)
val control1 = getControl1(preC2, p, p1, preRatio * rc)
val control2 = getControl2(p, p1, p2, angleRatio * rc)
preC2 = control2
preRatio = angleRatio
path.cubicTo(control1.x, control1.y, control2.x, control2.y, p1.x, p1.y)
}
}
}
}对于实时大量绘制的,频繁使用PointF可能挺浪费,自己写一个简单的Util循环回收就行了(注意:是实时大量绘制,几秒画一次的就别折腾复用了)
Kotlin
object Temps {
private val temps = arrayListOf<PointF>()
private val uses = arrayListOf<PointF>()
@MainThread
fun newTempPointF(x: Float, y: Float) = (temps.removeLastOrNull() ?: PointF()).apply {
set(x, y)
uses.add(this)
}
/**
* 请使用[useTempPointFs]
*/
@MainThread
fun endUse() {
temps.addAll(uses)
uses.clear()
"未知情况,缓存增长过大".throwIfDebug { temps.size > 500 }
}
}
/**
* 在回调域内调用[Temps.newTempPointF]获取临时对象,结束会自动回收
* 注意:切勿保存到回调外
*/
@MainThread
inline fun useTempPointFs(call: Temps.() -> Unit) {
call.invoke(Temps)
Temps.endUse()
}附效果图: