目录
一、积分上限函数与牛顿-莱布尼兹公式
(1)积分上限函数求导=积分符号内部的函数
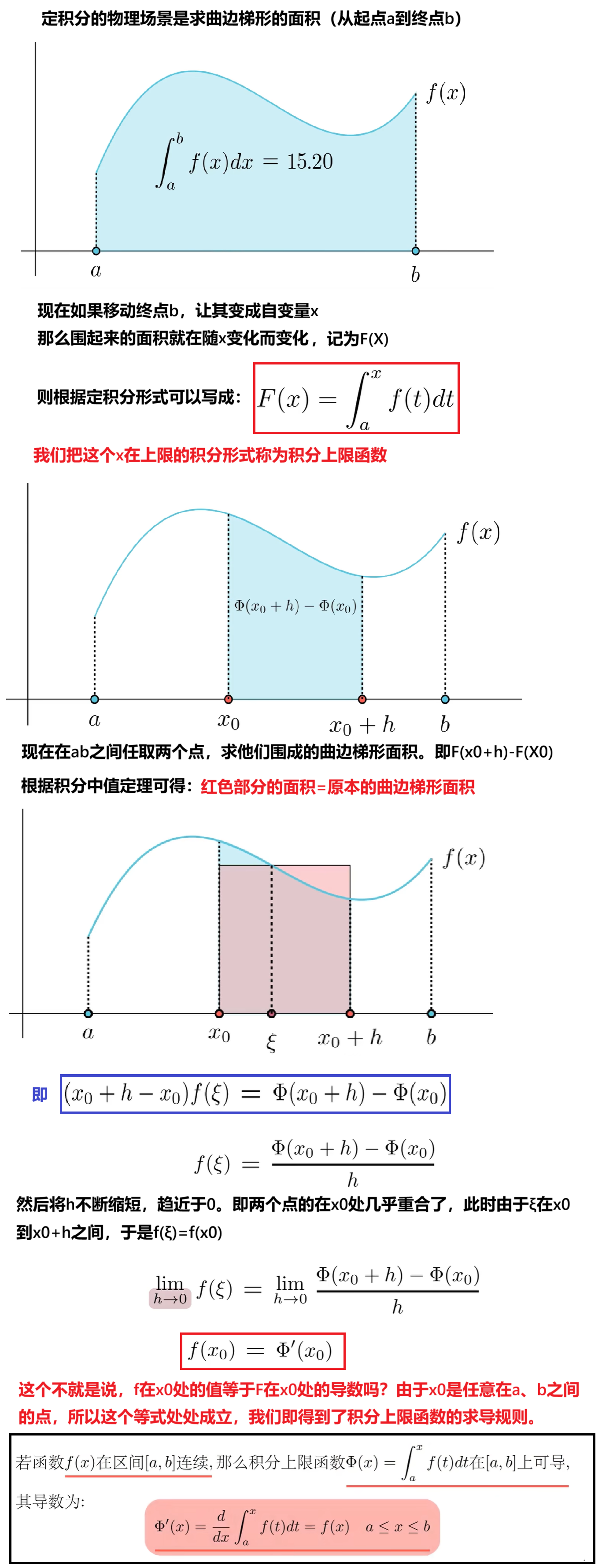
注意:这里我们说要求f(x)在区间zb内必须是连续的,才能有积分上限函数求导=f(x)的原函数成立。
(2)牛顿-莱布尼兹公式
根据上方的积分第一基本公式,可知:一个连续函数的一个原函数是对应的积分上限函数。而回忆刚刚证明积分上限函数中,F(x)的几何意义是不是就是围成曲边梯形的面积啊?

那么以后我们想求一个定积分时,按照定义是应当写成积分上限函数的形式,然后根据积分第一基本公式得到原函数相减的结果。但是积分上限函数是f(x)的一个原函数,而多个原函数之间只相差一个常数,这意味着我们只需要任意找到一个原函数求端点处的差值即可,并不需要找到那个所谓的积分上限函数。(在高等数学中我们也无法用任何函数成功构造该积分上限函数)
于是这个过程可以直接简化为:直接求出其原函数,然后将原函数在两个端点处的值相减即得到积分结果。
二、复数的原函数与不定积分
(1)参数方程法的缺点
回忆一下,我们前面文章中说一个复函数的积分求解方法:再判断该函数是否可以解析,如果不可解析(不可解析时积分结果与路径有关)则老老实实按照题目给定的路径,先化为两个曲线积分,然后对两个曲线积分用参数方程转换为单变量定积分问题。如果可以解析(路径无关)则化简路径,仍然转换为单变量定积分问题。

但是无论如何都无法避免使用参数方程形式下的单变量定积分问题,而这个被积函数往往十分复杂,不易于求解。
你可能说,我们还学了柯西积分定理,在一个闭合回路中,如何被积函数可解析,则结果等于0,这样更加简单。但是实际中不可能遇到的路径C都是闭合的,且被积函数也可能不解析。只要有任意一条不满足,都必须回过头使用原始的参数方程法。
(2)复数中莱布尼兹公式的使用条件
幸运的是,在复变函数中,我们有一个与实变函数非常相似的原函数概念。

**这个结论是革命性的!** 它意味着:
(1)积分与路径无关:只要起点和终点固定,无论路径 C如何弯曲、绕行,只要它完全包含在解析区域 D内,积分值都相同。
(2)计算极大简化:我们完全不需要再关心路径的具体形状,也无需进行复杂的参数化积分。计算复积分被简化为两步:
第一步:找到 f(z)的一个原函数 F(z)(这通常可以借鉴实变函数中的积分技巧)。
第二步:计算 F(z)在积分路径终点和起点的函数值之差。
值得注意的是:复函数的莱布尼兹公式同样需要满足可解析这个条件!
这是因为莱布尼兹公式本身是没有路径这个概念的,他原本是用在一元函数定积分的化简中,而一元函数的路径必定是x轴上的一条确定路径的线段。而在复数中,z=x+iy天然多出了路径的概念。所以想要让复数满足莱布尼兹公式,首先需要满足路径无关条件,即满足C-R方程。
然后关于这里要求单连通区域,其实就是路径无关的一个条件。根据格林公式中的理解:路径无关不能包含空洞在内,即不能是多连通区域。但是这只是最严格的要求,一般我们只需要保证局部单连通即可。
即路径无关=解析+单连通。
(3)总结
(1)对于可解析、闭合路径的复数求积分,直接用柯西积分定理得到0的结果
(2)对于可解析、但路径不闭合的复数求积分,既可以选择常规的参数方程化为一元函数定积分问题;还能直接使用牛顿-莱布尼兹公式求出原函数。
(3)对于既不解析,又路径不闭合的复数求积分,只能使用常规方法,先化为参数方程,再求一元函数定积分。
三、柯西积分公式
前面我们所有的讨论都是说:一条曲线路径在没有洞的情况下,可以使用复数领域的牛莱公式、或者柯西积分定理来求具体的结果。如果遇到了洞,就对洞画圈,将外圈积分转换为一个很小的绕洞积分。
但是绕洞积分仍然是一个表达式,而非具体的值。柯西积分公式就给出了该值具体应当是多少,将缺少的拼图补上了。

我们把这个等式成为柯西积分公式,它将一个包含奇点的逆时针闭合曲线积分(尽管这个被积函数看起来很奇怪,是f(z)/z-z0的形式),转换成了某个点的函数值相关结果。即这个函数的积分结果是2πi*f(z0)。