目录
前面我们学习了柯西积分公式,我们知道他的本质是一种特殊函数在有空洞(奇点)的情况下的求解方式,因为一条闭合曲线对一个解析函数进行回路积分得到的值为0,但是现在这个回路中包含了奇点,格林公式与柯西积分定理就失效了。于是我们将该特殊函数的闭合曲线积分与f(x)在奇点z0处的函数值建立了联系,从而基本解决了复数域中包含奇点的曲线积分问题。
一、高阶导数公式与柯西积分公式的联系
这里先提炼处柯西积分公式的意义:在研究一个函数f(z)时,如果我们想要研究某个具体的点z0处的函数值、及其n阶导数,都可以用柯西积分公式构造出一个特殊的闭合曲线积分形式,即用该曲线积分与该点的函数值完全等价。所以研究一个点处的函数值、变化率等情况变成了研究一个曲线积分。
即我们本来在研究一个点处的函数特性,现在升维成了研究一个曲线积分的特性。
(1)柯西积分公式:研究任意点的值转换成闭合曲线积分的值

虽然柯西积分公式最开始是为了解决闭合曲线内包含奇点的情况,但最后证明发现其普遍意义,即这个z0可以是f(z)函数上的任意一点,它表示了:函数f(z)在解析域上任意一点的取值,可以由从该点扩散开的闭合曲线积分得到。
注意,这里的z0必须是该被积函数的奇点,而不能是f(z)本身的奇点。看似z0具有任意性,但只要你选择了使用柯西积分公式,那么这个奇点就由被积函数决定且固定了。
换句话说,z0是你想观测的解析域内的任意点,于是你构造理了一个工具
去观测他;而如果你的工具确定了,那么你就只能观测这个特定的z0点,因为每一个工具都是不通用的,只能用来观测一个z0点。
正是因为解析域内任意一点的值完全可以由包围他的曲线积分得到,于是我们产生了一个自然的想法:能不能对这其进行求导看看他们之间的联系?也就是看看f(z)在z0点处的导数,是否也能由边界上的曲线积分来定义呢?
(2)解析函数的高阶导数:对曲线积分进行n次求导

这个公式的意义极为深刻:
他表示在解析域内的任何一点的函数值f(z0)都可以转换成围绕他的曲线积分的值。且在z0点处的任意阶导数值,竟然也与该曲线积分的任意阶导数完全一致!
那么以后在求一个函数f(z)在任意z点的值及其导数我们都可以转换成围绕他的任意正向闭合曲线的曲线积分值**(这个曲线积分的被积函数必须满足f(z)/z-z0的形式)。**
二、从高阶导到泰勒展开
(1)泰勒展开式的证明
泰勒级数的思想是用一个无穷级数在某一点逼近、拟合一个特定函数。如果这个拟合效果很好,则拟合函数与原函数之间的差值会逐渐减小直至0,即余项趋近于0。那么我们就说这个函数可以被泰勒展开。(也称为解析)。
 (2)收敛半径的求解
(2)收敛半径的求解
我们已经推导、证明了复数域的泰勒展开在形式上完全与实数域相同。

即z在一个以z0为圆心,半径为R的圆内,才能满足上述的几何级数展开范围。所以并不是我们规定了泰勒展开的区域一定是个圆域,而是只有是圆域才是能满足上述几何级数使用范围的最大区域。

那么以后在求一个泰勒级数的收敛半径时,我们有两种方式选择:
(1)找出函数 f(z)的所有奇点,计算它们到展开点 z0的距离,取最小值即为 R。
(2)用比值审敛法或者根值审敛法求幂级数的收敛半径。
三、洛朗级数
(1)洛朗级数是泰勒级数的解析域扩展形式
刚刚在研究泰勒级数展开时,我们推导出了f(z)的解析域必定是一个圆盘(即z的范围),而万一真的有一个环状区域呢?
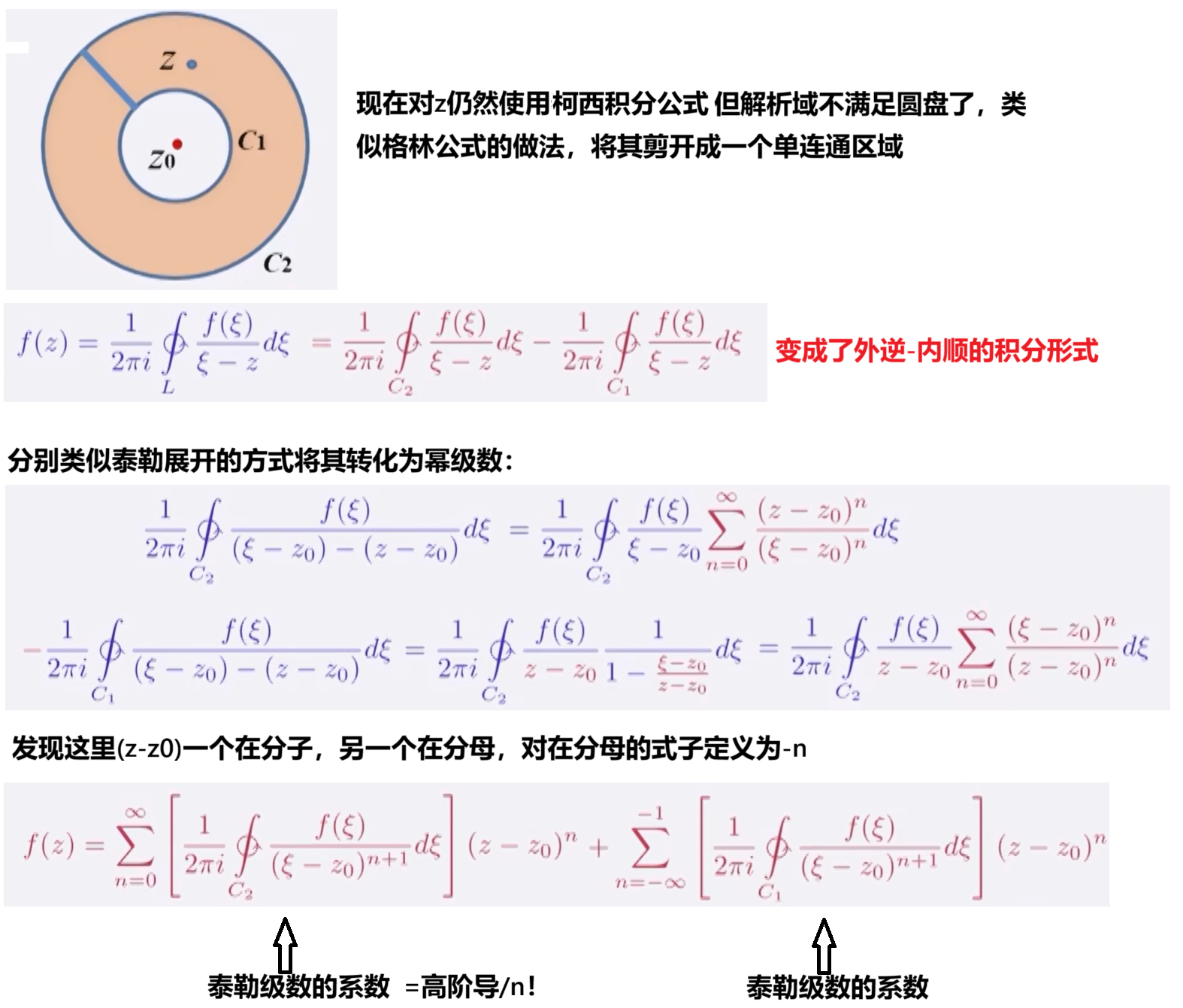
(2)收敛域的求解
类似泰勒级数求收敛半径的做法,可以从幂级数的定义出发,用比值审敛法、根值审敛法直接诶求解。
不过更加简单的仍然是,通过奇点的位置判断。内环半径是离内环收缩过程中碰到的第一个奇点,而外环半径是外环膨胀的过程中碰到的第一个奇点。