目录
一、傅里叶级数
你是否曾想过,任何一个复杂的周期函数(比如心跳曲线,音乐等)都能被拆解成一系列简单正余弦信号的叠加。在19世纪初,法国的数学家傅里叶提出了这样一个石破天惊的想法,现在傅里叶级数已经是现代信号处理、图像分析等领域的基石。
(1)为什么所有周期函数都能转换成傅里叶级数?
比方说,你现在要将这样一个周期脉冲信号用一些函数去进行拟合。而你的乐高中只有无数多个光滑的、周期性起伏的正余弦波形。虽然他们只有这一种基础形状,但是有着不同的大小(振幅)和起伏的速度(频率)。
从下图可以看出来:我们用的乐高越多,就越和原曲线拟合。那么我们有理由推断:任何一个周期函数,无论它多么的奇形怪状、崎岖不平,都能用无数个正余弦波积木给拟合出来。
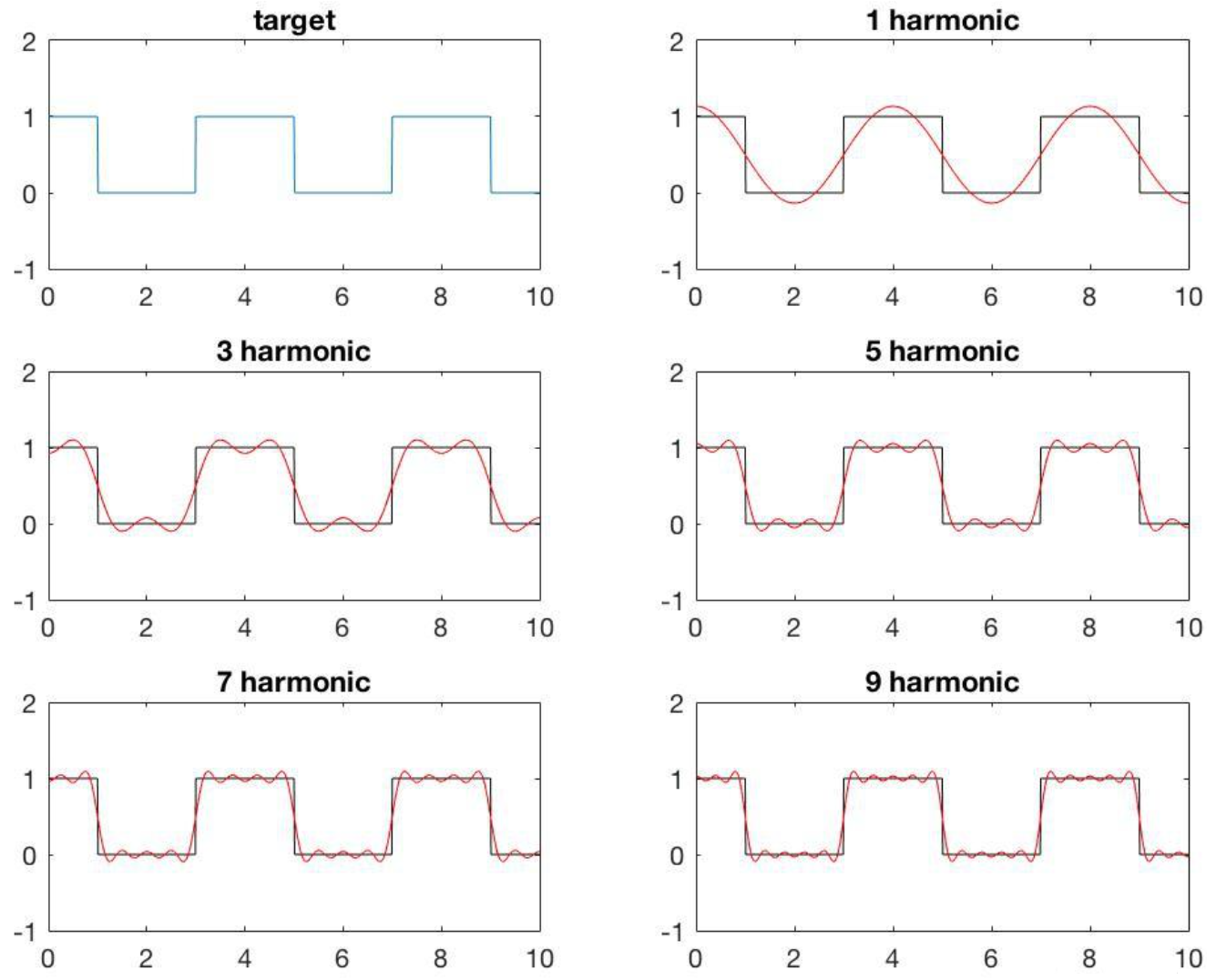
这听起来有些不可思议,但正余弦函数天然的周期性让他们的组合可以适配各种周期函数。同时振幅、频率的改变还让他们能适应各种曲折陡峭的山峰。
然而在数学上,傅里叶级数只有对于满足"狄利克雷条件"的周期函数才能正常转换(简单说,就是在一个周期内,函数本身不能有无限个间断点或趋于无穷大)。值得庆幸的是,我们在工程实践中遇到绝大多数周期信号都满足这个条件。这里的狄利克雷条件更多的是数学家们为了严格证明的存在,并不影响我们工程上的理解。
(2)傅里叶级数的一般形式
由于我们正是将无穷多个正余弦波形组装到一起才拟合出了原本想要的周期函数,我们把每一项都用通项的形式表示。然后将每一项的部分因子提出,写成较为简单的三角函数,对于这个提出的部分称为an、bn。
于是我们将任意一种周期函数化为了三角函数叠加的形式,但是关于如何求解每一项的系数an、bn、a0具体的值,我们在下一节讲述。
(3)三角函数的正交性(筛选性)
如果两个不同频率的正弦波(或余弦波)在一个周期内相乘再积分的结果为零,我们就说它们正交。经过数学家的严格证明,发现任何一个正余弦函数和其余任何函数都呈现正交性,即给定任意三角函数,任何两个不相同的项乘积并在一个周期内求积分等于0;任何两个完全相同的项乘积并在一个周期内求积分等于T/2。

我们利用这样的性质可以制作一个专有筛子:对an用cosnx作为筛子;对bn用sinnx作为筛子,由于只可能出现两种情况:f(x)中含有cosnx、f(x)中不含有cosnx。当不含有的时候积分结果为0;当含有的时候我们对其相乘然后在一周期内求积分得到的结果是系数*T/2。
这个筛选过程非常精准,但筛子本身有一个'固有损耗':任何成分通过它都会被缩放为原来的
T/2倍。因此,为了从筛选结果中还原出该成分真实的'浓度'(即系数aₙ或bₙ),我们需要进行'归一化'操作,即将积分结果乘以2/T。这样,我们就能得到准确的配方了。
当然,还有另外一种理解方式:把原周期函数想象成一个含有不同浓度的饮料,该饮料由cosnx、sinnx的不同种类原料勾兑而成,每一种原料的含量不同。现在你已知了最终的饮料f(x),对每一种原料用特殊的筛子筛选(一种筛子只能筛出一种原料及其浓度),于是你就可以精准的知道该饮料中含有什么原料。
而由于筛子有一定损失(筛选比例是固定值T/2),所以筛选得到的结果想要得到真正的浓度,需要给他归一化,对每个结果乘上2/T即可得知饮料中是否含有某种原料,及其浓度。
于是给出通项求法:

当然,这里也可以把a0理解成在该周期函数不波动时候的静态分量、直流分量,所以令n=0就表示该函数的频率为0不波动。
二、傅里叶积分与傅里叶积分变换
在前面,我们用傅里叶级数对有周期性的函数进行了拟合,并且使用的正余弦乐高积木越多,拟合程度也就越好。并且还用筛子的比喻直观体现了如何求解每一项的系数an、bn。
但是现实世界中的大量信号,就是非周期的(比如一个脉冲信号、一段语音、一幅图像)。那么对于这些一生只绽放一次的花朵,是否还能用傅里叶的思想来拟合呢?
答案是肯定的,傅里叶积分将傅里叶级数的思想从周期函数推广到非周期函数的强大工具。其核心思想是:将非周期函数看作是周期为无穷大的周期函数。
为了实现这一点,傅里叶积分还会引入复指数的概念,因为复指数能极大程度的简化三角函数的运算,并且还能承载三角函数本身的周期性,所以一个复指数只会对应一个实数域的三角函数,即复指数起到的根本作用就是简化计算。然而我们一般不会将其结果再转换回实数三角函数域中,因为比较复杂,所以我们以后会将复数纳入常规方法中,但始终要记得复指数本质对应了实数的三角函数,我们物理世界所关心的幅度、相位可以从复数中提取出实数信息。
(1)傅里叶级数的复指数形式

(2)系数统一化、形式统一化
由于上面的式子看起来很丑,不方便记忆与分析,我们现在将系数统一。

由此,我们就将实数域中的傅里叶级数形式完美的转化成了复数域下的级数,且在复数域下,形式是高度统一的,无论是系数,还是形式都完美统一 (而实数三角函数的形式下,系数有个2倍关系,还有sin、cos的差异,十分杂乱)。
(3)傅里叶变换、傅里叶逆变换

对于这样一个完整的过程,我们称为傅里叶逆变换;而中间部分我们单拎出来令其为F(w),因为它关τ积分后,只剩下w这一个变量,中间部分我们称为傅里叶变换。
而从表达式中可以看出,傅里叶变换将原本只关于τ的函数变成了只关于w角速度的函数, 然而工程中常常把w替换为2πf,即傅里叶变换完成了从时域到频域的转换。(时间函数->频率函数)。
而反过来傅里叶逆变换就是将原本只关于w或者f的函数回归到只关于时间t的函数,即傅里叶逆变换完成了从频域到时域的转换。(频率函数->时间函数)
最后可以看到在时域频域转换时会多出一个系数1/2π,每个教材上关于系数的划分都不同,有的将其划分到傅里叶变换中,有的将其划分到逆变换中,而还有的将其开方,一边一半。我们不需要在意他到底是怎么定义的,只要关心一点:系数只改变幅值,而不影响周期。
三、傅里叶积分公式、变换的三角表示形式
上面我们给出了傅里叶积分公式、傅里叶积分变换的一般表达式,它是一个复指数形式的。但是如果f(t)有奇偶性的话,则能极大程度的化简一般式,变为傅里叶余弦积分形式、傅里叶正弦积分形式。
(1)傅里叶积分公式的三角形式

即由于外层对w积分时,只把w看做变量,而其他都看做常数,由定积分的偶倍奇零可知:一般形式的傅里叶积分公式展开后只剩下余弦项(实部项),而正弦项(虚部项)由于是关于w的奇函数,积分结果为0。
后面我们讨论的余弦积分公式、正弦积分公式都是在一般三角形式上推导得到的。
(2)傅里叶正弦积分公式
刚刚我们讨论了外层积分对w奇偶性的作用,还未曾讨论内层函数对f(τ)的奇偶性作用。
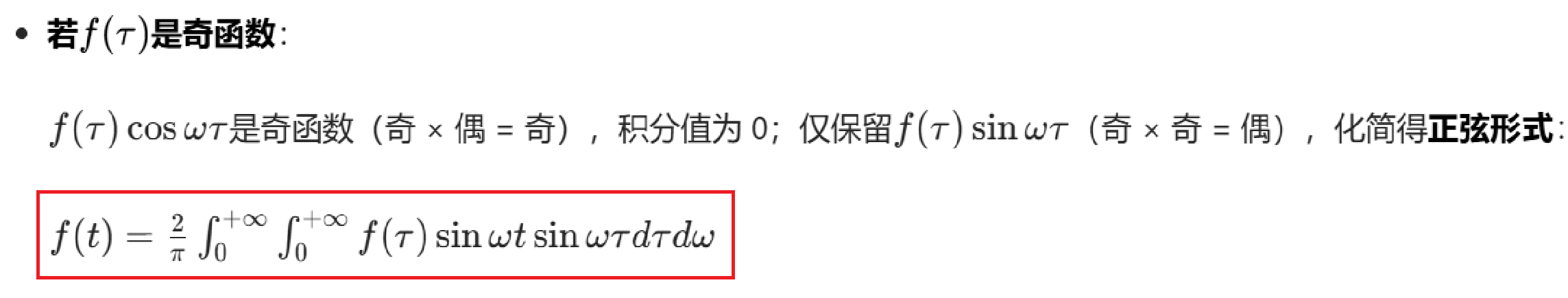
(2)傅里叶余弦积分公式
同理可得:

关于傅里叶积分公式的正余弦形式,通常能帮我们快速做题。但其实我们并不需要记得多么清楚,只需要明白他是从一般三角形式利用奇偶性化简、转换得到的即可,我们需要熟练掌握转换方法,而不是死记硬背。
总结一下:如果积分符号里面是复指数形式,则必定要使用欧拉公式;如果积分符号里面没有任何复指数,才能直接积分,而不选择用欧拉公式。当然如果是含有复数,但却不是复指数形式,则二者皆可。不过我们还是推荐欧拉公式,只有极少数情况复数可以直接当做系数提出去。