| 转换类型 | 步骤描述 |
|---|---|
| 树转化为二叉树 | 1. 连接兄弟节点 :将树中每个节点的所有子节点用指针连接起来,形成一个子节点链。 2. 保留第一个子节点 :对于每个节点,只保留其与第一个子节点的指针,并删除与其他子节点的指针。 3. 调整指针:将每个节点的第一个子节点作为二叉树中的左子节点,将同一节点的下一个兄弟节点作为二叉树中的右子节点。 |
| 森林转换为二叉树 | 1. 转换每棵树 :将森林中的每棵树分别转换为二叉树(使用树转化为二叉树的方法)。 2. 连接二叉树:将第一棵二叉树的根作为最终二叉树的根,然后将第二棵二叉树的根作为第一棵二叉树根的右子节点,第三棵二叉树的根作为第二棵二叉树根的右子节点,依此类推,直到所有二叉树连接完毕。 |
| 二叉树转换为树 | 1. 识别根节点 :将二叉树的根作为树的根。 2. 处理左子节点 :将二叉树的左子节点转换为树的子节点(递归处理左子树)。 3. 处理右子节点 :将二叉树的右子节点转换为树的兄弟节点(递归处理右子树)。 注意:此转换仅适用于原本由树转换而来的二叉树,否则可能无法形成有效的树结构。 |
| 二叉树转换为森林 | 1. 断开右链 :从二叉树的根开始,沿右子节点链依次断开指针,每个右子节点对应森林中的一棵树。 2. 转换每棵二叉树 :将断开后的每个二叉树(包括根和左子树)转换为树(使用二叉树转换为树的方法)。 3. 形成森林:这些树组成了森林。 |
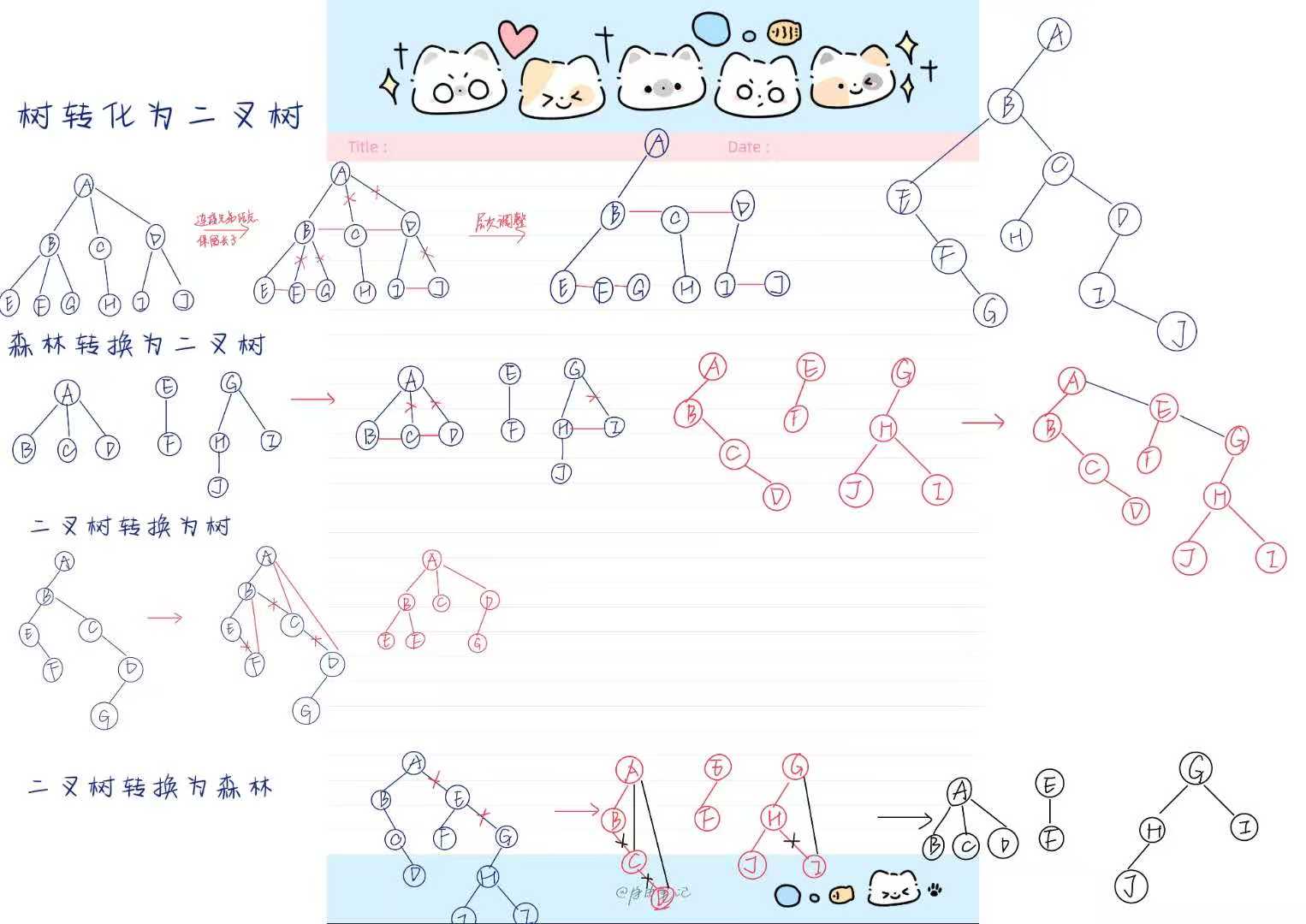
-
树转化为二叉树:核心是"左孩子右兄弟",即左指针指向第一个子节点,右指针指向下一个兄弟节点。
-
森林转换为二叉树:森林是多棵树的集合,转换时先将每棵树转换为二叉树,然后通过右指针连接。
-
二叉树转换为树:逆过程,将左指针恢复为子节点,右指针恢复为兄弟节点。
-
二叉树转换为森林:通过断开右指针链,将一棵二叉树分解为多棵二叉树,再分别转换为树。
| 类别 | 核心知识点与步骤 | 关键性质与考点 | 真题常见问法 |
|---|---|---|---|
| 树 → 二叉树 | 核心:"左孩子,右兄弟" 1. 连线 :在所有兄弟节点 之间加一条线。 2. 删线 :对于每个节点,只保留它与第一个孩子 的连线,删除它与其他孩子之间的线。 3. 旋转:以树的根节点为轴心,将整棵树顺时针旋转约45度,使层次分明。 | 对应关系 : • 二叉树的左分支 → 树中的长子 。 • 二叉树的右分支 → 树中的兄弟 。 • 根节点必然没有右孩子 (因为树的根没有兄弟)。 考点 : • 转换后的二叉树形态。 • 原树中某节点在二叉树中的位置(例如,问某个堂兄弟在二叉树中变成了什么关系)。 | "将一棵树T转换为二叉树BT,则BT的根节点......" "下列关于树与二叉树的转换中,正确的是......" |
| 森林 → 二叉树 | 核心:先单转,后连根 1. 单转 :将森林中的每一棵树分别转换为二叉树。 2. 连根 :从第一棵二叉树开始,将后一棵二叉树的根节点 作为前一棵二叉树根节点的右孩子,用线连接起来。 | 对应关系 : • 二叉树根节点的右子树 → 森林中除第一棵树外剩下的树 。 • 后续转换规则与"树→二叉树"一致。 考点 : • 森林中树的棵数 = 二叉树根节点及其右链上的节点总数。 • 给定森林,求转换后二叉树的中序序列。 | "由3棵树组成的森林,其转换得到的二叉树中,根节点......" "设森林F对应二叉树B,若B的根节点有右孩子,则F包含......" |
| 二叉树 → 树 | 核心:逆"左孩子,右兄弟" 1. 连线 :若某节点i有左孩子,则将该左孩子以及该左孩子右链上的所有节点 都与节点i连线。 2. 删线 :删除原二叉树中所有节点与其右孩子 的连线。 3. 整理:层次化排列,形成树结构。 | 前提 :该二叉树必须是由一棵树 转换而来(即根节点无右子树)。 考点 : • 判断一棵二叉树能否还原为一棵树(根节点不能有右孩子)。 • 还原后树中节点的父子、兄弟关系。 | "将二叉树T转换为一棵树后,节点A是节点B的......" |
| 二叉树 → 森林 | 核心:断右链,再单转 1. 断根右链 :从二叉树的根节点开始,断开其与右孩子的连线 ,然后递归地断开其右子树中每个节点的右链。 2. 单转 :将得到的每一棵独立的二叉树 分别转换为树。 3. 这些树即构成了原来的森林。 | 对应关系 : • 二叉树根节点的右孩子 → 森林中第二棵树的根 。 • 断开右链后,每一棵独立的二叉树对应森林中的一棵树。 考点 : • 给定二叉树,求森林由几棵树构成(数根节点右链上的节点数+1)。 • 二叉树的前序、中序遍历与森林的遍历关系。 | "将二叉树B转换为森林F,则F中包含多少棵树?" "设二叉树B是由森林F转换而来,若对B进行中序遍历,相当于对F进行......" |
遍历对应关系(极高频考点)
森林的先序遍历 ↔ 其对应二叉树的先序遍历。
- 原因:两者访问顺序都是"根 -> 子树 -> 兄弟树",结构一致。
森林的中序遍历 ↔ 其对应二叉树的中序遍历。
- 原因:森林的中序遍历定义为"遍历第一棵树的子树 -> 访问第一棵树的根 -> 遍历剩余的森林",这恰好对应二叉树中的"左子树 -> 根 -> 右子树"。
注意:树没有中序遍历,但森林有。
节点关系与数量关系
叶子节点数 :在"树 -> 二叉树"的转换中,原树的叶子节点在二叉树中一定没有左孩子(因为叶子没有孩子,自然没有长子)。
树的度:树中某节点的度,等于其在对应二叉树中该节点的左孩子及其右链上的节点总数。
森林的树个数 :等于对应二叉树中根节点加上其右链上的节点总数。
解题技巧与易错点
核心是理解"左孩子,右兄弟":所有转换和性质都源于此。在做题时,可以在草稿上快速画出简单的转换图来辅助推理。
区分"树"和"森林":题目中明确是"一棵树"还是"森林"至关重要,这决定了转换后的二叉树根节点是否有右子树。
警惕"堂兄弟"关系:在原树中是堂兄弟的两个节点,在转换后的二叉树中可能一个在另一个的子树中,关系变得不直观,这是选择题的常见陷阱。
遍历序列的应用:当题目给出遍历序列时,先利用"森林的先/中序与其二叉树的先/中序相同"这一性质,在二叉树结构上进行分析,通常会大大简化问题。
- 遍历:按照某种次序把所有结点都访问一遍。
- 层次遍历:基于树的层次特性确定的次序规则
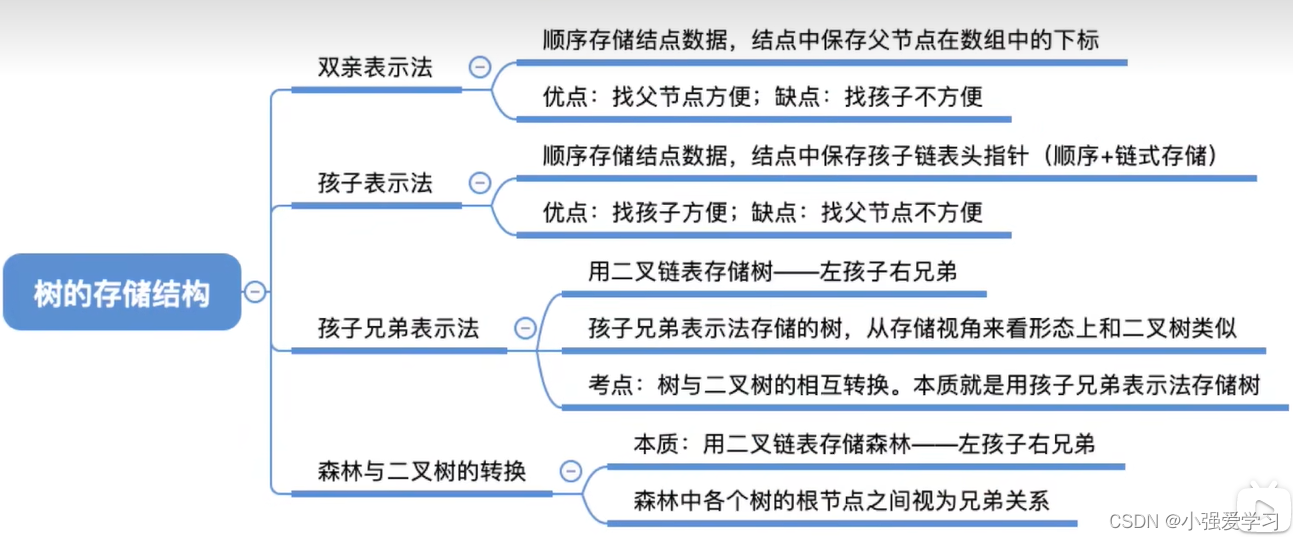
树和森林的遍历
树的先根遍历
若树非空,先访问根结点,再依次对每棵子树进行先根遍历;(与对应二叉树的先序遍历序列相同)
树的先根遍历序列与这棵树相应二叉树的先序序列相同。
树的后根遍历
若树非空,先依次对每棵子树进行后根遍历,最后再访问根结点。(深度优先遍历)
树的后根遍历序列与这棵树相应二叉树的中序序列相同。
层序遍历(队列实现)
- 若树非空,则根结点入队;
- 若队列非空,队头元素出队并访问,同时将该元素的孩子依次入队;
- 重复以上操作直至队尾为空;
森林的遍历
- 先序遍历:等同于依次对各个树进行先根遍历;也可以先转换成与之对应的二叉树,对二叉树进行先序遍历;
- 中序遍历:等同于依次对各个树进行后根遍历;也可以先转换成与之对应的二叉树,对二叉树进行中序遍历;
二叉树的遍历
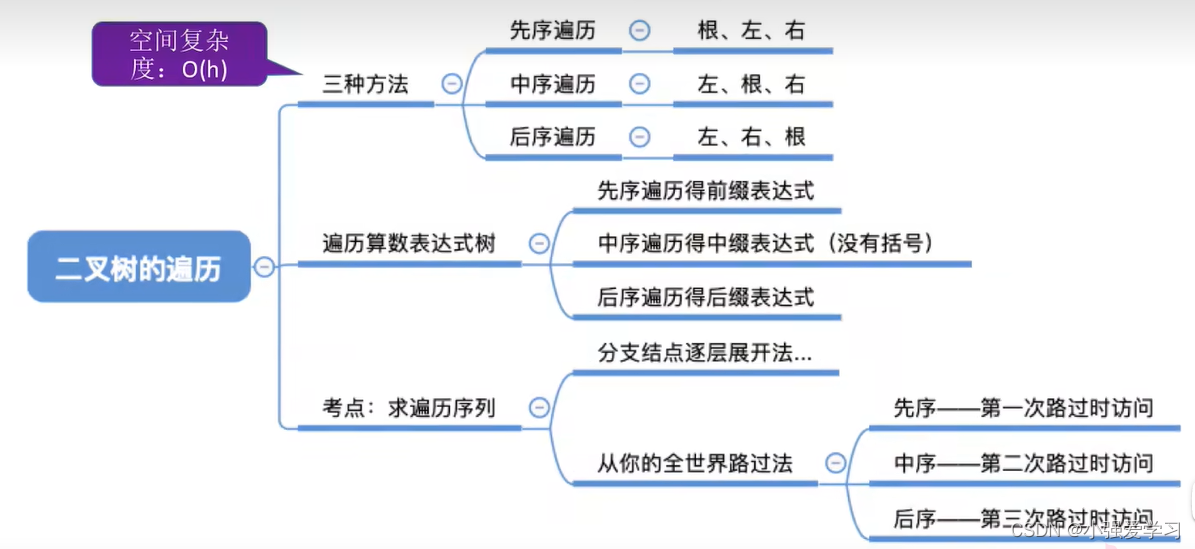


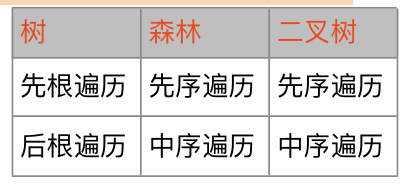
- 树的后根遍历相对于树来说是后序遍历,相当于其对应的二叉树来说是中序遍历
- 森林的中序遍历实际上是对森林后序遍历,其结果等价于对应二叉树的中序遍历

-
为什么"先序"全都等价?
-
树与二叉树:树的先根遍历(访问根,然后依次先根遍历每个子树),应用"左孩子右兄弟"规则转换后,正好对应二叉树先序遍历(访问根,然后遍历左子树(原长子),最后遍历右子树(原兄弟))。
-
森林与二叉树:森林的先序遍历(访问第一棵树的根,先序遍历第一棵树的子树森林,先序遍历剩余森林),转换后同样对应二叉树的先序遍历。
-
-
为什么"树的后根"等于"二叉树的中序"?
- 这是最容易混淆的点。树的后根遍历 是"先依次后根遍历每棵子树,最后访问根"。在转换后的二叉树中,这个"访问根"的动作,恰好发生在"遍历完左子树(原所有子树)之后,遍历右子树(原兄弟树)之前",这正是二叉树中序遍历的定义。