对python的再认识-基于数据结构进行-a003-列表-排序

Python 列表排序

本文聚焦 Python 列表的排序操作，包含 sort() 与 sorted() 的对比、自定义排序、多级排序、排序稳定性及性能分析。

我也将给出个人思维导图

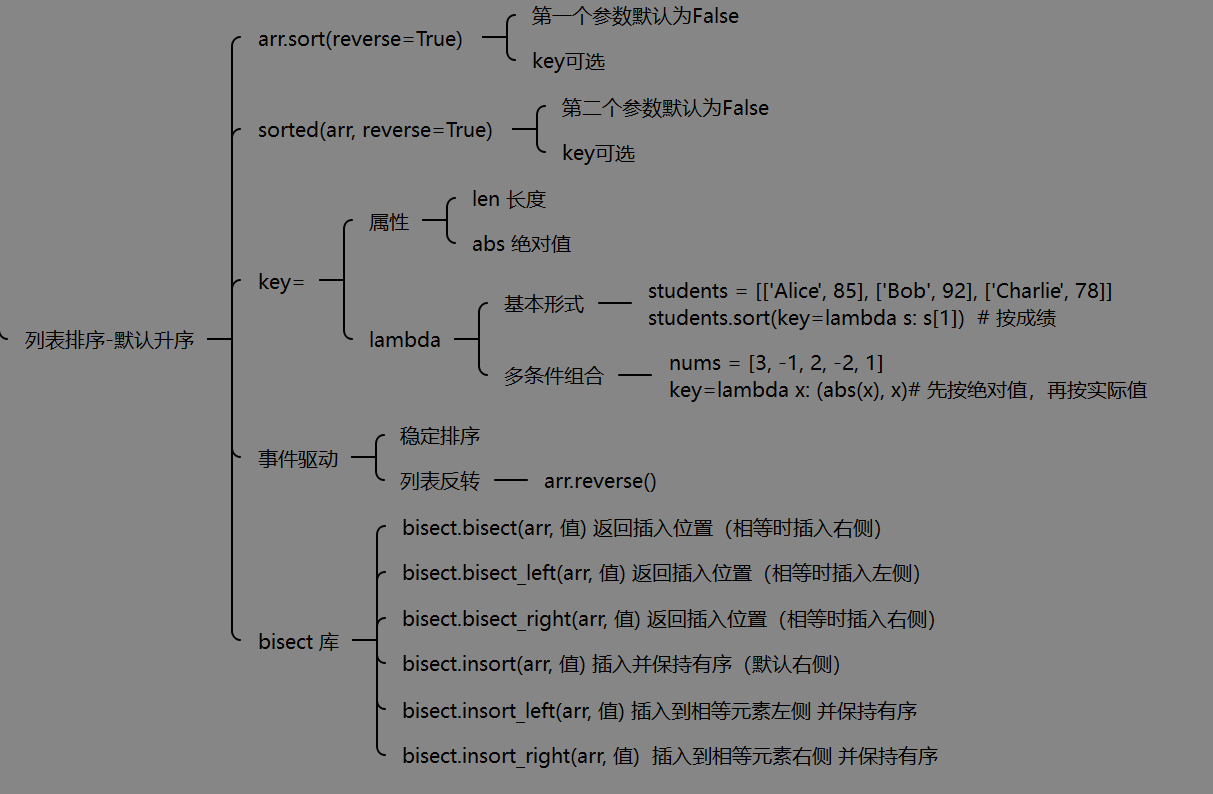
一、基础用法

1.1 sort() vs sorted()

方法	类型	返回值	是否修改原列表
list.sort()	方法	None	是（原地排序）
sorted(list)	内置函数	新列表	否

nums = [3, 1, 4, 1, 5, 9]

# sort() - 原地排序
nums.sort()
print(nums)  # [1, 1, 3, 4, 5, 9]
# sort() 返回 None
result = nums.sort()
print(result)  # None

# sorted() - 返回新列表
nums = [3, 1, 4, 1, 5, 9]
sorted_nums = sorted(nums)
print(sorted_nums)  # [1, 1, 3, 4, 5, 9]
print(nums)         # [3, 1, 4, 1, 5, 9] - 原列表不变

注意 ：sort() 返回 None 是有意设计，强制开发者区分原地操作和返回新值。

1.2 反向排序

nums = [3, 1, 4, 1, 5, 9]

# 方法 1：reverse 参数
nums.sort(reverse=True)
# [9, 5, 4, 3, 1, 1]

# 方法 2：sorted + reverse
nums = [3, 1, 4, 1, 5, 9]
desc = sorted(nums, reverse=True)
# [9, 5, 4, 3, 1, 1]

# 方法 3：先排序再反转（不推荐，多一次操作）
nums = [3, 1, 4, 1, 5, 9]
nums.sort()
nums.reverse()
# [9, 5, 4, 3, 1, 1]

1.3 字符串列表排序与字典序

字典序（Lexicographic Order）：从左到右逐字符比较，Unicode 码点小的排在前面。

# 基础字典序排序
words = ['banana', 'apple', 'cherry']
words.sort()
# ['apple', 'banana', 'cherry']

# 大小写敏感（ASCII: 'A'=65, 'a'=97）
words = ['banana', 'Apple', 'cherry']
words.sort()
# ['Apple', 'banana', 'cherry'] - 大写字母排在前面

# 数字 < 大写 < 小写
chars = ['9', 'A', 'a', 'Z', 'z']
chars.sort()
# ['9', 'A', 'Z', 'a', 'z']
# ASCII: '9'=57, 'A'=65, 'Z'=90, 'a'=97, 'z'=122

# 前缀相同，短的排在前面
words = ['a', 'aa', 'aaa']
words.sort()
# ['a', 'aa', 'aaa']

# 不区分大小写
words = ['banana', 'Apple', 'cherry']
words.sort(key=str.lower)
# ['Apple', 'banana', 'cherry']

# 按最后一个字符排序
words = ['abc', 'def', 'xyz']
words.sort(key=lambda s: s[-1])
# ['abc', 'def', 'xyz']  # c < f < z

注意 ：不同类型元素的列表无法排序，会抛出 TypeError。

---

二、自定义排序

2.1 key 参数

key 指定一个函数，用于提取比较键：

# 按字符串长度排序
words = ['python', 'java', 'c', 'javascript']
words.sort(key=len)
# ['c', 'java', 'python', 'javascript']

# 按绝对值排序
nums = [3, -5, 2, -1, 4]
nums.sort(key=abs)
# [-1, 2, 3, 4, -5]

# 按字符串中数字部分排序
items = ['item123', 'item45', 'item6']
items.sort(key=lambda s: int(s[4:]))
# ['item6', 'item45', 'item123']

# 按倒数第二字符排序
words = ['abc', 'xyz', 'def']
words.sort(key=lambda s: s[-2])
# ['abc', 'def', 'xyz']

2.2 使用 lambda 函数

# 按嵌套列表的某个元素排序
students = [['Alice', 85], ['Bob', 92], ['Charlie', 78]]
students.sort(key=lambda s: s[1])  # 按成绩
# [['Charlie', 78], ['Alice', 85], ['Bob', 92]]

# 复杂排序逻辑
files = ['report.pdf', 'data.csv', 'notes.txt']
files.sort(key=lambda s: s.split('.')[-1])  # 按扩展名
# ['data.csv', 'notes.txt', 'report.pdf']

# 按数值部分排序（忽略前缀）
items = ['ver1.10', 'ver1.2', 'ver1.1']
items.sort(key=lambda s: [int(x) for x in s[3:].split('.')])
# ['ver1.1', 'ver1.2', 'ver1.10']

2.3 多条件组合

# 先按长度，再按字母序
words = ['aa', 'b', 'aaa', 'ab', 'a']
words.sort(key=lambda s: (len(s), s))
# ['a', 'b', 'aa', 'ab', 'aaa']

# 先按绝对值，再按实际值
nums = [3, -1, 2, -2, 1]
nums.sort(key=lambda x: (abs(x), x))
# [-1, 1, -2, 2, 3]

---

三、多级排序

3.1 利用稳定性多次排序

Python 排序是稳定的，相等元素保持原顺序。利用这一点可实现多级排序：

# 学生：姓名、年龄、成绩
students = [
    ['Alice', 20, 85],
    ['Bob', 22, 85],
    ['Charlie', 20, 92],
    ['David', 22, 78]
]

# 先按二级排序键（年龄）
students.sort(key=lambda s: s[1])
# 再按一级排序键（成绩）
students.sort(key=lambda s: s[2], reverse=True)
# 结果：
# [['Charlie', 20, 92]]      # 成绩最高
# [['Alice', 20, 85]]        # 成绩相同，年龄小的在前（稳定性）
# [['Bob', 22, 85]]          # 成绩相同，年龄大的在后
# [['David', 22, 78]]        # 成绩最低

3.2 使用元组键（推荐）

students = [
    ['Alice', 20, 85],
    ['Bob', 22, 85],
    ['Charlie', 20, 92],
]

# 按成绩降序、年龄升序
students.sort(key=lambda s: (-s[2], s[1]))
# [['Charlie', 20, 92], ['Alice', 20, 85], ['Bob', 22, 85]]

# 按成绩升序、年龄升序、姓名升序
students.sort(key=lambda s: (s[2], s[1], s[0]))

优势：一次排序完成，更高效清晰。

3.3 三级及以上排序

# 记录：部门、职位级别、入职时间、姓名
records = [
    ['IT', 3, 2020, 'Alice'],
    ['HR', 2, 2019, 'Bob'],
    ['IT', 3, 2021, 'Charlie'],
    ['IT', 2, 2020, 'David'],
]

# 按部门 → 级别（降序）→ 入职时间
records.sort(key=lambda r: (r[0], -r[1], r[2]))
# [['HR', 2, 2019, 'Bob'],
#  ['IT', 2, 2020, 'David'],
#  ['IT', 3, 2020, 'Alice'],
#  ['IT', 3, 2021, 'Charlie']]

---

四、排序稳定性

4.1 稳定排序的含义

稳定排序：相等元素的相对顺序在排序后保持不变。

# 示例：按分数排序，同分保持原顺序
students = [
    ['Alice', 85],
    ['Bob', 92],
    ['Charlie', 85],
]

students.sort(key=lambda s: s[1])
# [['Alice', 85], ['Charlie', 85], ['Bob', 92]]
# Alice 原本在 Charlie 前面，排序后依然在前

4.2 实际应用场景

# 任务：优先级、创建顺序
tasks = [
    ['Task C', 'high', 2],
    ['Task A', 'low', 1],
    ['Task B', 'high', 1],
]

# 先按创建时间排序
tasks.sort(key=lambda t: t[2])
# [['Task A', 'low', 1],
#  ['Task B', 'high', 1],
#  ['Task C', 'high', 2]]

# 再按优先级排序（利用稳定性）
tasks.sort(key=lambda t: t[1], reverse=True)
# [['Task B', 'high', 1],  # 同优先级，Task B 原本在前
#  ['Task C', 'high', 2],
#  ['Task A', 'low', 1]]

---

五、特殊场景

5.1 列表反转

nums = [1, 2, 3, 4, 5]

# reverse() - 原地反转
nums.reverse()
# [5, 4, 3, 2, 1]

# 切片反转 - 创建新列表
nums = [1, 2, 3, 4, 5]
reversed_nums = nums[::-1]
# [5, 4, 3, 2, 1]
print(nums)  # [1, 2, 3, 4, 5] - 原列表不变

5.2 bisect 库：有序列表插入

bisect 是 Python 标准库，用于在已排序列表中高效查找和插入。

import bisect

nums = [1, 3, 5, 7, 9]

# bisect_left：返回插入位置（相等时插入左侧）
pos = bisect.bisect_left(nums, 5)
print(pos)  # 2（索引 2，5 的位置）

# bisect_right：返回插入位置（相等时插入右侧）
pos = bisect.bisect_right(nums, 5)
print(pos)  # 3（索引 3，5 之后）

# bisect：别名，等同于 bisect_right（更常用）
pos = bisect.bisect(nums, 5)
print(pos)  # 3

插入操作：

nums = [1, 3, 5, 7, 9]

# insort：插入并保持有序（默认右侧）
bisect.insort(nums, 4)
# [1, 3, 4, 5, 7, 9]

# insort_left：插入到相等元素左侧
bisect.insort_left(nums, 5)
# [1, 3, 4, 5, 5, 7, 9]

# insort_right：插入到相等元素右侧
bisect.insort_right(nums, 5)
# [1, 3, 4, 5, 5, 5, 7, 9]

函数	作用	相等元素位置
bisect	查找插入位置	右侧
bisect_left	查找插入位置	左侧
bisect_right	查找插入位置	右侧
insort	插入并保持有序	右侧
insort_left	插入并保持有序	左侧
insort_right	插入并保持有序	右侧

注意 ：bisect 是 bisect_right 的别名，insort 是 insort_right 的别名，两者更常用。
时间复杂度：查找 O(log n)，插入 O(n)（需要移动元素）

---

六、性能分析

6.1 算法：Timsort

Python 使用 Timsort 算法（结合归并排序和插入排序）：

特性	说明
时间复杂度	O(n log n) 最坏/平均
空间复杂度	O(n) 额外空间
稳定性	稳定排序
适应性	对部分有序数据效率高（接近 O(n)）

6.2 性能对比

import timeit

TEST_SORT = "nums = list(range(1000000, 0, -1)); nums.sort()"
TEST_SORTED = "sorted(list(range(1000000, 0, -1)))"
TEST_REVERSE = "nums = list(range(1000000)); nums.reverse()"

操作	时间复杂度	空间复杂度	说明
list.sort()	O(n log n)	O(1)	原地排序
sorted(list)	O(n log n)	O(n)	创建副本，占用更多内存
list.reverse()	O(n)	O(1)	原地反转
切片 [::-1]	O(n)	O(n)	创建新列表
bisect.insort()	O(n)	O(1)	插入（查找 O(log n)）
bisect.bisect()	O(log n)	O(1)	仅查找位置

6.3 性能建议

场景	推荐方法	原因
原列表可修改	list.sort()	节省内存
需保留原列表	sorted(list)	不破坏原数据
已排序列表插入元素	bisect.insort()	O(n) vs O(n log n)
只需要反向	list.reverse()	O(n) 原地操作

---

七、最佳实践

7.1 选择排序方法

# 场景 1：需要修改原列表
nums = [3, 1, 2]
nums.sort()  # 推荐

# 场景 2：需要保留原列表
nums = [3, 1, 2]
sorted_nums = sorted(nums)  # 推荐

# 场景 3：链式操作
nums = [3, 1, 2]
result = sorted(nums)[:3]  # sorted 支持链式

# 场景 4：只检查排序，不实际排序
nums = [1, 2, 3]
all(nums[i] <= nums[i+1] for i in range(len(nums)-1))  # True

7.2 常见错误

# 错误 1：忽略 sort() 的返回值
nums = [3, 1, 2]
sorted_nums = nums.sort()  # sorted_nums 是 None！
# 正确
nums.sort()
sorted_nums = nums

# 错误 2：修改排序后再排序
nums = [3, 1, 2]
nums.sort().reverse()  # AttributeError: 'NoneType'
# 正确
nums.sort(reverse=True)

# 错误 3：对不兼容类型排序
mixed = [1, 'a', 2]
mixed.sort()  # TypeError

7.3 代码风格建议

原则	好的写法	不好的写法
原地排序	nums.sort()	nums = sorted(nums)
保留原值	sorted_nums = sorted(nums)	nums_copy = nums[:]; nums_copy.sort()
多级排序	sort(key=lambda x: (-x[0], x[1]))	两次 sort 调用
反转	nums.reverse()	nums = nums[::-1]（当不需要保留原值）

---

八、总结

方面	要点
sort()	原地排序，返回 None，修改原列表
sorted()	返回新列表，原列表不变，支持链式操作
key 参数	指定比较键，支持 lambda 自定义逻辑
稳定性	Python 排序稳定，可用于多级排序
算法	Timsort，O(n log n)，稳定且高效
最佳实践	原地用 sort()，保留原值用 sorted()