【LeetCode刷题】二叉树的直径

给你一棵二叉树的根节点，返回该树的直径。

二叉树的直径是指树中任意两个节点之间最长路径的长度。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的长度由它们之间边数表示。

示例 1：

复制代码

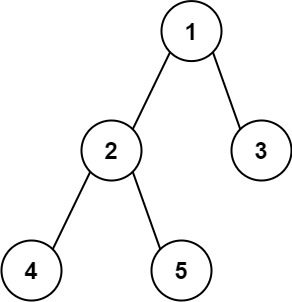
输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

复制代码

输入：root = [1,2]
输出：1

提示：

树中节点数目在范围 [1, ] 内
-100 <= Node.val <= 100

解题思路

二叉树的直径是任意两个节点之间的最长路径长度（边数） ，这条路径可能经过根节点，也可能不经过。对于每个节点，其能贡献的最长路径是左子树深度 + 右子树深度（路径经过该节点），我们需要遍历所有节点，找到这个值的最大值。

递归逻辑

深度计算 ：定义辅助函数_depth(node)，计算节点node的深度（从该节点到叶子节点的最长边数）。
- 空节点深度为 0；
- 非空节点的深度 = 左右子节点深度的最大值 + 1（当前节点到子节点的一条边）。
直径更新 ：在计算深度时，每个节点的左右深度之和就是 "经过该节点的最长路径长度"，用全局变量max_diameter维护所有节点的该值的最大值。
结果返回 ：最终max_diameter就是二叉树的直径。

示例验证（输入`root = [1,2,3,4,5]`）

节点 4/5 是叶子，深度为 0；
节点 2 的左深度 = 0+1=1，右深度 = 0+1=1，左右深度之和 = 2（路径 4-2-5，长度 2）；
节点 3 是叶子，深度为 0；
节点 1 的左深度 = 1+1=2（2 到 1 的边），右深度 = 0+1=1（3 到 1 的边），左右深度之和 = 3（路径 4-2-1-3，长度 3）；
最终max_diameter=3，与示例输出一致。

算法复杂度

时间复杂度：O(n)（遍历所有节点一次，每个节点仅计算深度一次）；
空间复杂度：O(h)（h为树的高度，递归栈的深度由树高决定；最坏情况树为链状，h=n）。

Python代码

python 复制代码

from typing import Optional, List, Deque
from collections import deque


# 二叉树节点定义
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        # 初始化最大直径为0
        self.max_diameter = 0
        # 递归计算深度，同时更新最大直径
        self._depth(root)
        return self.max_diameter

    def _depth(self, node: Optional[TreeNode]) -> int:
        """辅助函数：计算节点的深度（边数），并更新最大直径"""
        if not node:
            return 0
        # 递归计算左右子树的深度
        left_depth = self._depth(node.left)
        right_depth = self._depth(node.right)
        # 核心：当前节点的左右深度之和 = 经过该节点的最长路径长度（边数）
        self.max_diameter = max(self.max_diameter, left_depth + right_depth)
        # 返回当前节点的深度：子树最大深度 + 1（当前节点到子节点的一条边）
        return max(left_depth, right_depth) + 1


# ---------------------- 辅助函数 ----------------------
def build_tree(nums: List[Optional[int]]) -> Optional[TreeNode]:
    """层序构建二叉树（适配LeetCode数组表示法）"""
    if not nums or nums[0] is None:
        return None
    root = TreeNode(nums[0])
    q: Deque[TreeNode] = deque([root])
    idx = 1
    while q and idx < len(nums):
        cur = q.popleft()
        if nums[idx] is not None:
            cur.left = TreeNode(nums[idx])
            q.append(cur.left)
        idx += 1
        if idx < len(nums) and nums[idx] is not None:
            cur.right = TreeNode(nums[idx])
            q.append(cur.right)
        idx += 1
    return root


# ---------------------- 测试用例验证 ----------------------
if __name__ == "__main__":
    sol = Solution()
    # 示例1输入：root = [1,2,3,4,5]
    root = build_tree([1, 2, 3, 4, 5])
    print(f"二叉树的直径：{sol.diameterOfBinaryTree(root)}")

LeetCode提交代码