个人疑问笔记,不会涉及公式推导,也不会解释步骤间的具体连接,只是记录一些卡住我的点
1.首先有贝尔曼算子/方程/公式如下:
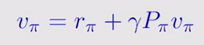
产生问题:就算每个state的π都确定,想要知道每个state 的v也是十分困难的.这里我学的教程给了一种迭代法求v,下面介绍一下为什么可以用来求解.
2.如果π确定其实,贝尔曼算子就是v=f(v)的方程且符合压缩映射的条件,从而获得两个有用的信息:
(1)有解且是唯一解(2)可以采用迭代法求出这个解,迭代越多越接近.
3.以上是π固定的情况,但是我们需要的是π不确定的情况也能讨论,即找到最优π,贝尔曼公式被更新为两个未知数的:
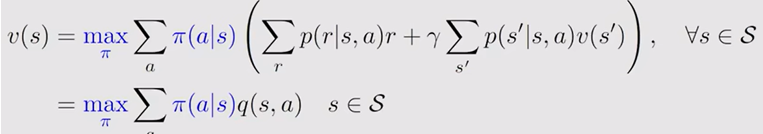
可以看到q是一个数字,π是条件概率和为1.因此只要选择最大的q令其概率等于1得到的v就是最大的,这就可以完成最优性.按照这个方法选定策略的话就可以把未知量又变回只剩v一个.
4.引入:各个state的策略互相影响其q值,目前选择了q值最大的为π不代表他就是全局最大的.
而且已知(1)对于某次的v确定则最优π确定(2)目标是π*和v*(3)注意到贝尔曼公式里p概率为环境属性并不会变化,而π则是数字,为了最优性他固定为1,真正的变量为a*
(4)目标求解方程为: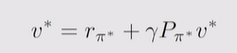
,假定π*已知,想要求解这个方程显然随便给个v0即可.然后不停迭代最后会得到v*的近似值,而后面会讲怎么得到这个假定的π*
5.值迭代求解v*,这里的值不是实际的value只是一个代入贝尔曼公式得到的数字.
(1)一次迭代的v求解方法
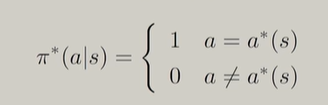因此可以得到一次迭代时的v求解方法为: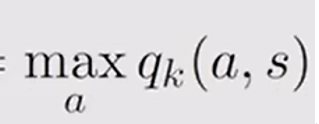
而q的求法是:
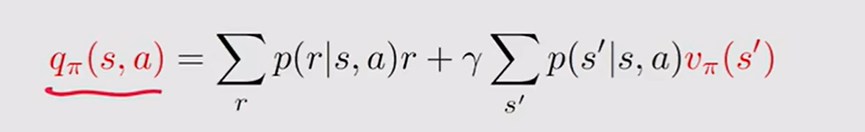
但是得到q需要vπs'的情况.这就体现了值迭代的特点了,v不value只是一个任意数字,因此最开始的q可以得到哪怕策略不知道
(2)求出一次迭代的数字后安装压缩映射的迭代方法显然: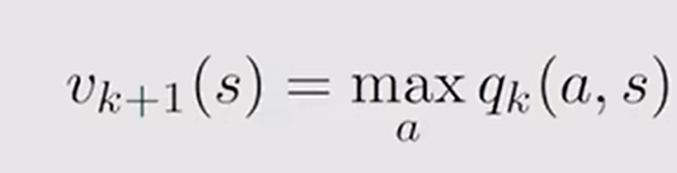
(3)π是选择q最大的,因此每次迭代过程中的π也是可知道的,因此迭代到最后也就顺带求出来了π*
6.下面讲策略迭代:
(1)π0初始已知,因此可以得到
这个贝尔曼公式,对这个贝尔曼公式直接用迭代法可以得到vπ0的值(实际不可能迭代无穷次,因此采用的为截断策略迭代,满足误差要求就停止).
(2)有了vπ0自然就解决了q0的确定问题.为啥解决了q0的确定问题很重要呢?因为实际上还是要求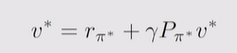这个问题,值迭代是假定了最终π已经存在,因此把他看做普通的v=f(v),而策略迭代则是正视了存在两个变量的问题,存在两个迭代过程每次迭代过程都会动态产生新的要求解的压缩映射问题
(3)π0确定是为v0=f(v0)然后得到π1,进而变成v1=f(v1)问题.
(4)他们虽然原理不同但是求解流程步骤存在相似处:
