一阶惯性环节

一阶惯性环节的传递函数：

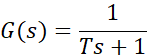
频率特性：

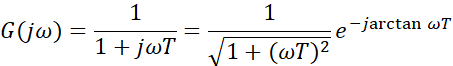
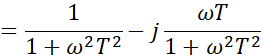
幅频特性：

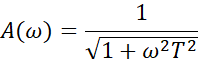
相频特性：

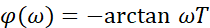
对数幅频特性：

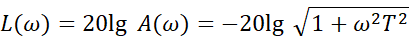
对数相频特性：

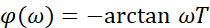
首先分析对数幅频特性曲线的大致形状。

（1）当 ω ≪1/T 时，对数幅频特性可近似为

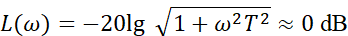
（2）当 ω ≫1/T 时，对数幅频特性可近似为

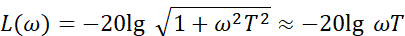
惯性环节的对数幅频特性渐进曲线 近似为两段直线，交点处频率 ω = 1/T ，称为转折频率 ，高频部分是斜率为****-20dB/dec 的直线 ，Bode 图如图所示。注意ω 处为转折频率，在转折频率的地方相角特性在-45° ，在10ω 处才到-90° 。这里两条直线仅为渐进线，在转折频率处误差最大，为-3dB。

R和C的并联可以看作一阶惯性环节和比例环节的串联，其中T=RC 。

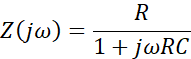
对于Nyquist图来说，是一个半径为R/2 的半圆 ，C在这里对半圆的形状没有影响，影响是曲线弯曲的快慢，转折频率ω =1/T ，此时相角特性为 -45 ° ，如果C 很小，需要在很高的频率下才会起到作用 ，呈现出类似半圆的形状，在低频下，C可以看作断路，所以在Nyquist上始终是一个点。比如，我们绘制RC并联阻抗的Nyquist图，取R=100 Ω ，C=1.59nF ，此时转折频率为1MHz。

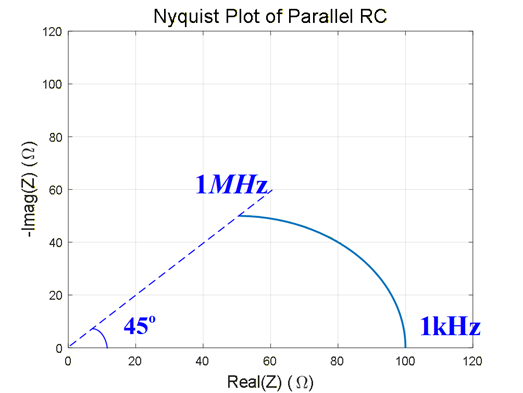
Matlab 复制代码

clc; clear; close all;
% ====== RC 并联参数 ======
R = 100;          % 电阻 (Ω)
C = 1.57e-9;         % 电容 (F)

% ====== 频率范围 ======
f = logspace(1, 6, 200);  % 10 Hz ~ 1 MHz
w = 2*pi*f;

% ====== RC并联阻抗 ======
Z = 1 ./ (1/R + 1j*w*C);

% ====== 绘制 Nyquist ======
figure(1);
plot(real(Z), -imag(Z), 'LineWidth', 1.5);   % Nyquist: x=Re(Z), y=-Im(Z)
xlim([0 120])
ylim([0 120])

grid on; 
title('Nyquist Plot of Parallel RC','FontSize',16);
xlabel('Real(Z) (\Omega)','FontSize',14);
ylabel('-Imag(Z) (\Omega)','FontSize',14);

figure(2);
semilogx(f,imag(Z));
grid on;