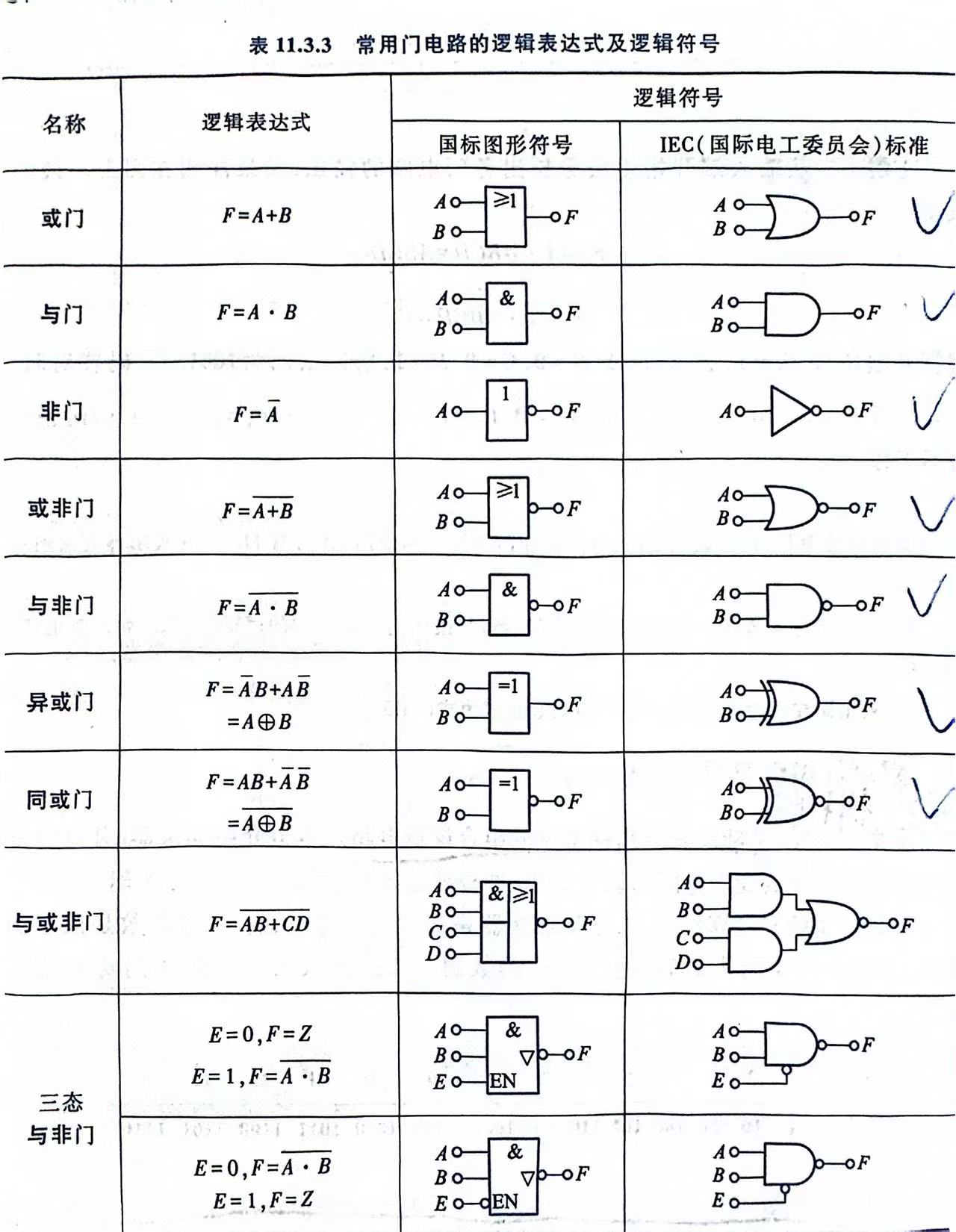
基本逻辑电路
1.与门（AND Gate）
当所有输入均为高电平时，输出才为高电平。逻辑表达式是**Y = A·B。**真值表如下
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2.或门（OR Gate）
只要有一个输入为高电平，输出即为高电平。逻辑表达式是 Y = A+B。真值表如下
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
3.非门（NOT Gate）
输出信号与输入信号相反。逻辑表达式为Y = ¬A。真值表如下
| A | Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
4.与非门（NAND Gate）
与门的输出经过非门处理。逻辑表达式Y = ¬(A·B)。真值表如下
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
5.或非门（NOR Gate）
或门的输出经过非门处理。逻辑表达式Y = ¬(A + B)。真值表如下
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
6.异或门（XOR Gate）
当两个输入不同时，输出为高电平。逻辑表达式Y = A ⊕ B。真值表如下
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
7.同或门（XNOR Gate）
当两个输入相同时，输出为高电平。逻辑表达式Y = ¬(A ⊕ B)。真值表如下
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
加法器
1.半加器(half-adder)
半加器是一种不考虑低位来的进位数，只能对本位上的两个二进制数求和的组合电路。其真值表如下，A,B是两个求和的二进制数，F是相加后得到的本位数，C是相加后得到的进位数。
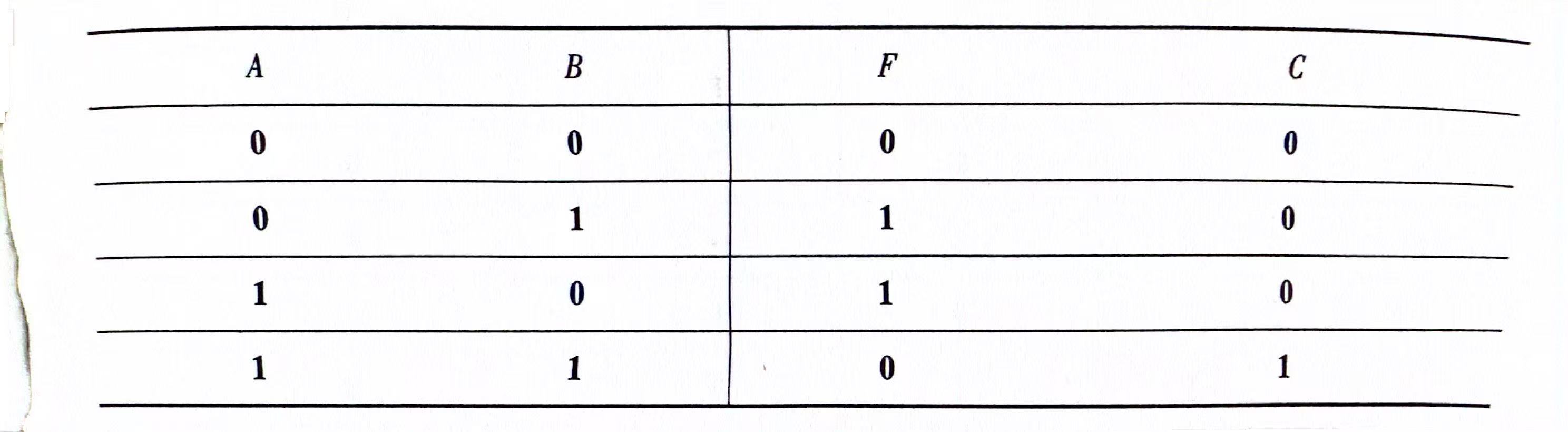
由上述真值表可以看出A和B相同时F为0，A和B不同时F为1，这是异或门的逻辑关系。只有A和B都为1时C才为1，这是与门的逻辑关系。所以半加器是由一个异或门和一个与门组成，半加器电路和逻辑符号如下
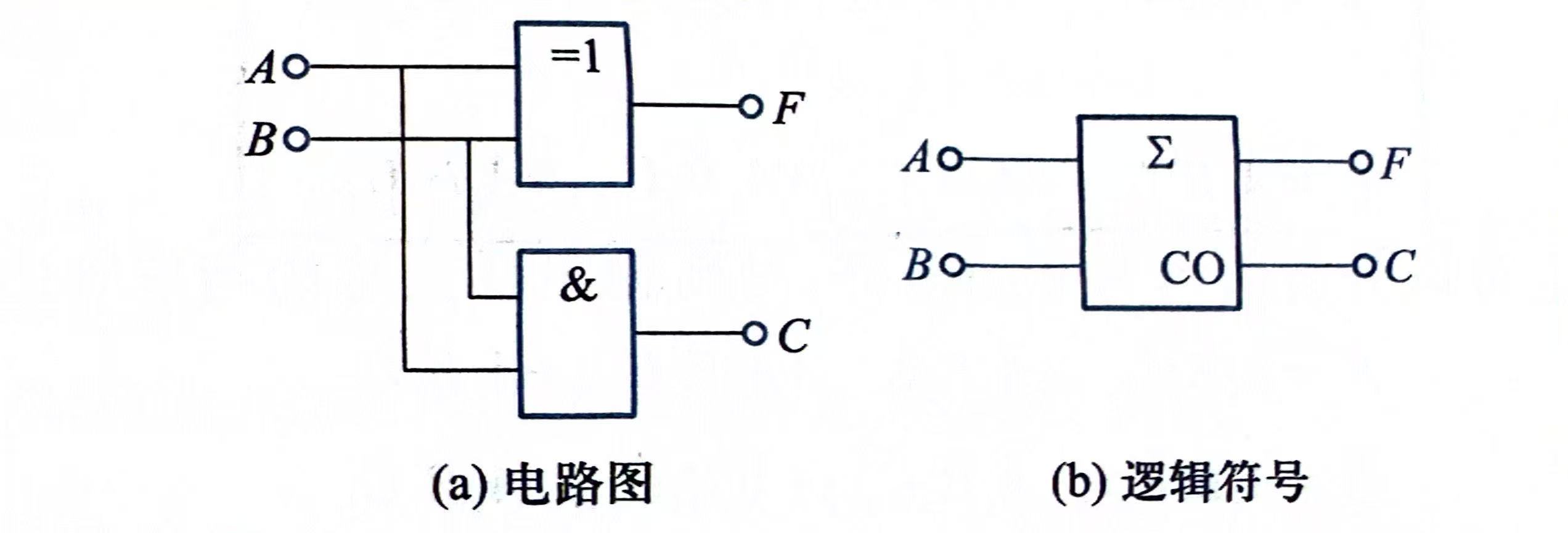
半加器电路图IEC标准如下(一个异或门一个与门)
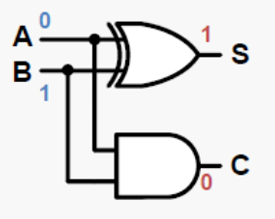
2.全加器(full-adder)
全加器是一种将低位来的进位数连同本位的两个二进制数三者一起求和的组合电路。根据这一逻辑功能列出的真值表如下。Ai和Bi是本位的二进制数，Ci-1是来自低位的进位数，Fi是相加后得到的本位数，Ci是相加后得到的进位数。
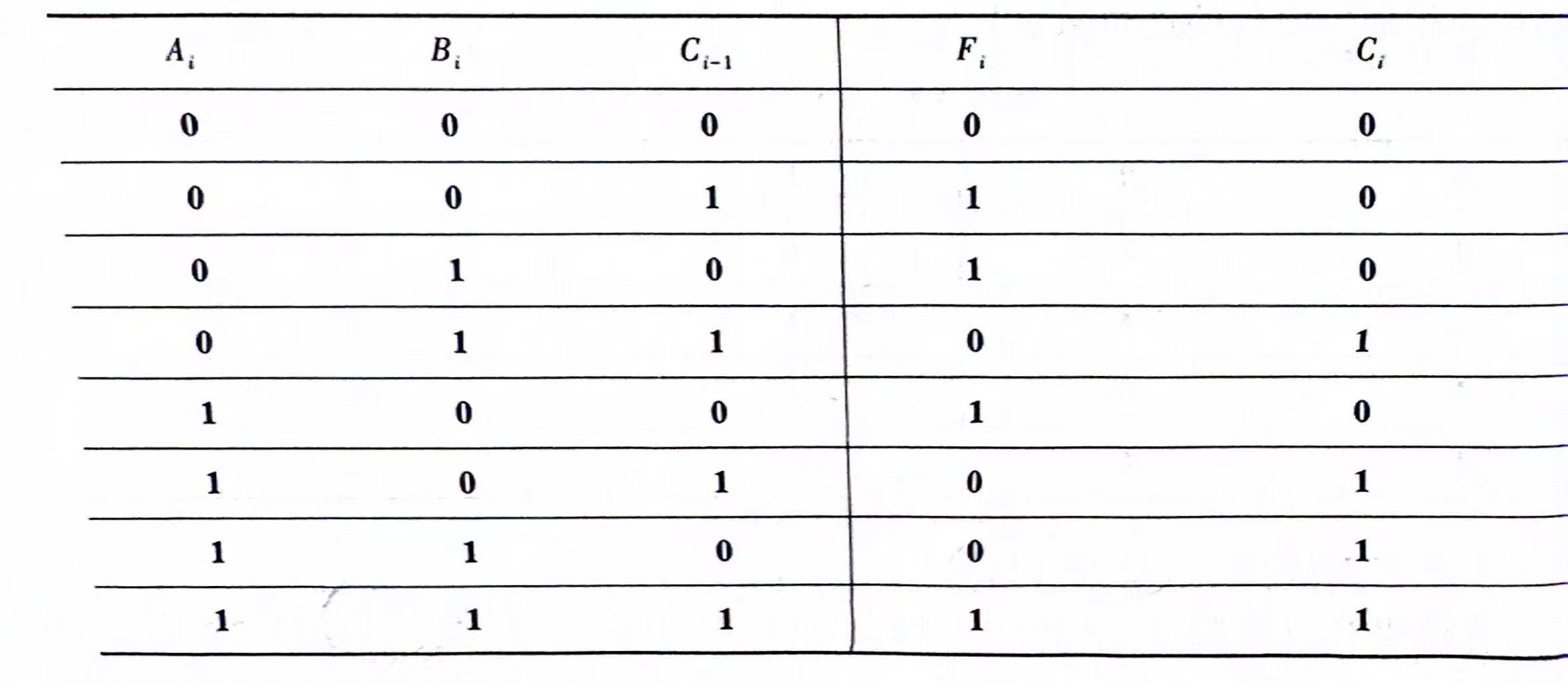
接下来根据真值表写出逻辑表达式，但是全加器不像半加器真值表那样一目了然。可采用如下方法：先分析输出为1的条件，将输出为1各行中的输入变量为1者取原变量，为0者取反变量，再将它们用与的关系写出来。
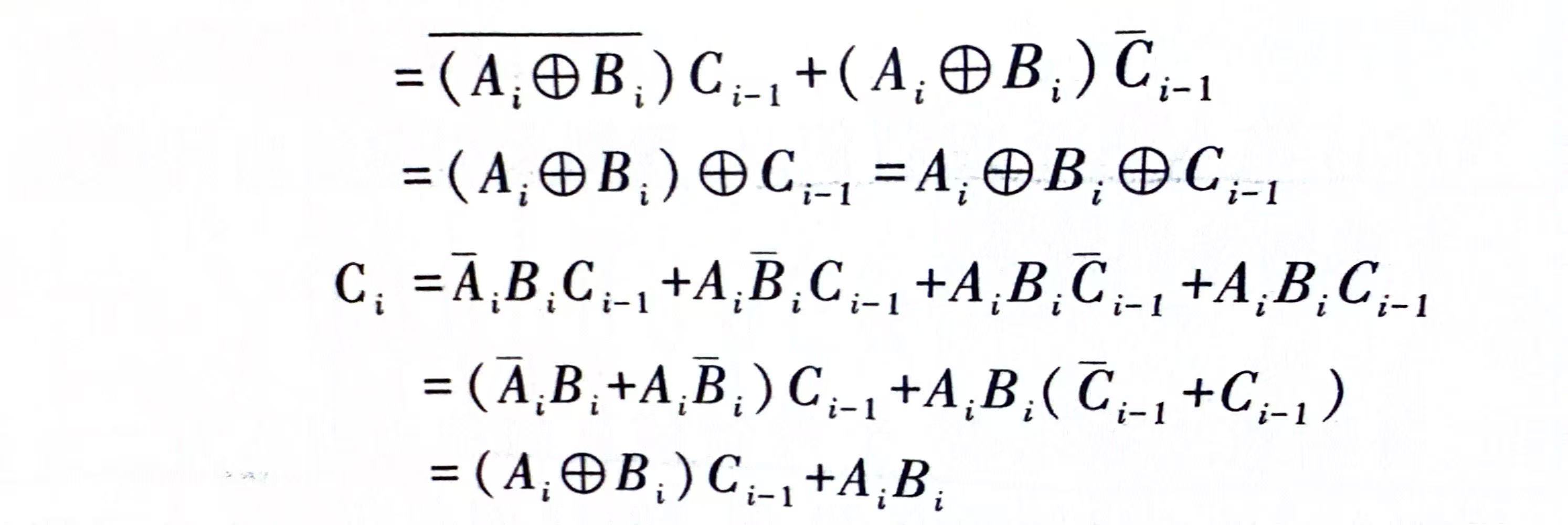
根据化简后的公式可以画出全加器电路即逻辑符号如下所示。以上是通过逻辑公式化简得到的结果。根据电路图也可以直观理解全加器，实际上就是当前位的Ai和Bi先相加(半加器)，得到的当前位再与来自低位的进位数Ci-1相加得到最终的当前位Fi，所以当前位Fi上的计算就是三个数经过两个半加器计算得到的([(A+B)+C])。对于下一位Ci，要么是0要么是1，如果0的话代表Ai+Bi+Ci-1这三个数加起来都没有超过2，即没有进位，如果为1的话，意味着Ai+Bi(第一个半加器)或Ci-1+(Ai+Bi)(第二个半加器)中有一个半加器进位了，所以用或门来得到最后的进位数Ci
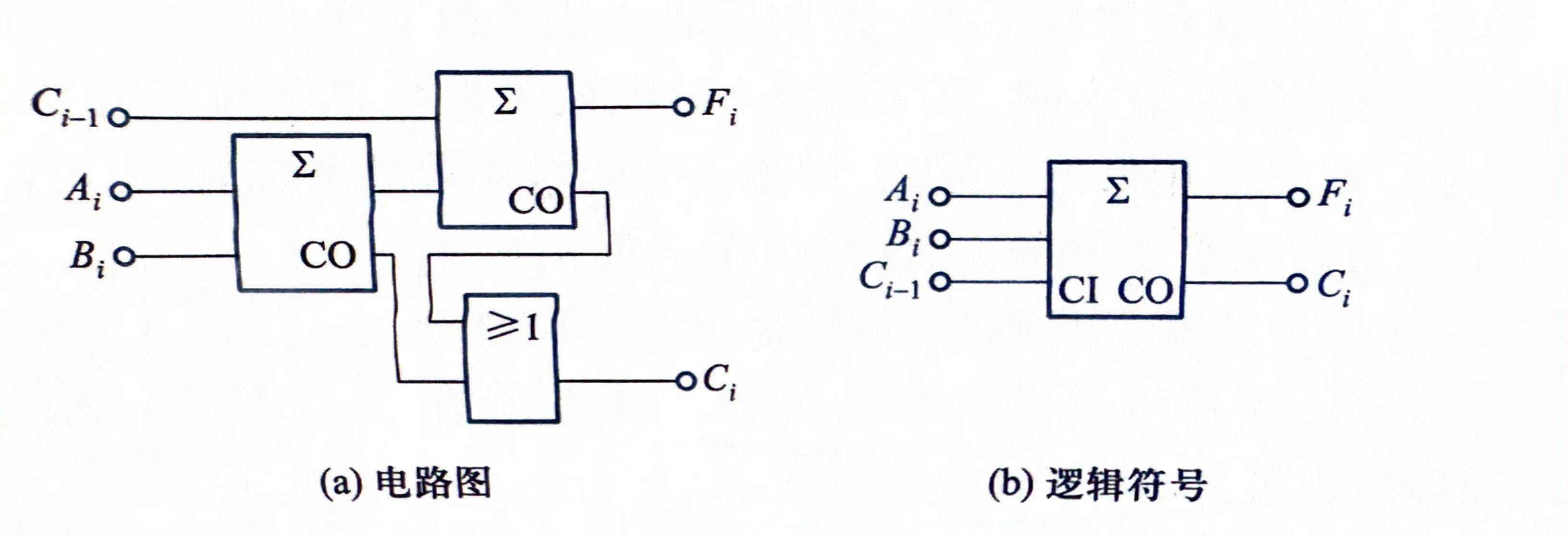
全加器电路图IEC标准如下
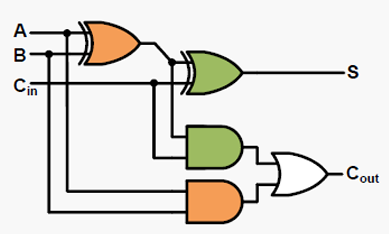
3.多位加法器(全加器级联)
能够实现多位二进制加法运算的电路称为多位加法器。在一位加法器的基础上，组成多位加法器时，主要是考虑进位方式问题。进位方式有两种，即逐位进位(又称串联进位) 和**超前进位(又称并联进位)。**逐位进位的4位加法全加器如下图所示，它由4个全加器串联组成。
逐位进位
逐位进位（cascaded carry），又称串联进位或行波进位（RCA），是一种通过串联全加器实现多位数相加的电路方法。其逻辑结构简单，但由于高位运算必须等待低位进位信号逐级传递，导致运算速度较慢。
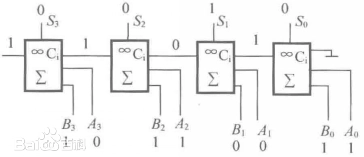
逐位进位的4位加法全加器如下图所示，它由4个全加器串联组成。如输入的被加数A为0101，加数B为1101，得和数S为(C3=1)0010（实际上结果应该是10010，只不过这里只写出了本位Fi，而最高位1为进位数）。这种加法器在进行任一位加法运算时，都必须等到比它低位的加法运算结束送来进位时才能进行。运算的进位，是从低位向高位以串形方式逐位进位。这种串行加法器电路虽然简单，由于最高位的运算一定要等到所有的低位运算都完成并送来进位信号时才能进行，运算速度慢，一般用于对运算速度要求不高的设备中。要求提高运行速度，应尽量缩短高位形成的全加和的时间，可选取超前进位全加器。
超前进位
超前进位加法器(Carry-lookahead adder [1])是对普通的全加器进行改良而设计成的并行加法器，主要是针对普通全加器串联时互相进位产生的延迟进行了改良。超前进位可以同时计算出所有的进位数，而不需要等待低位计算完才得到进位数
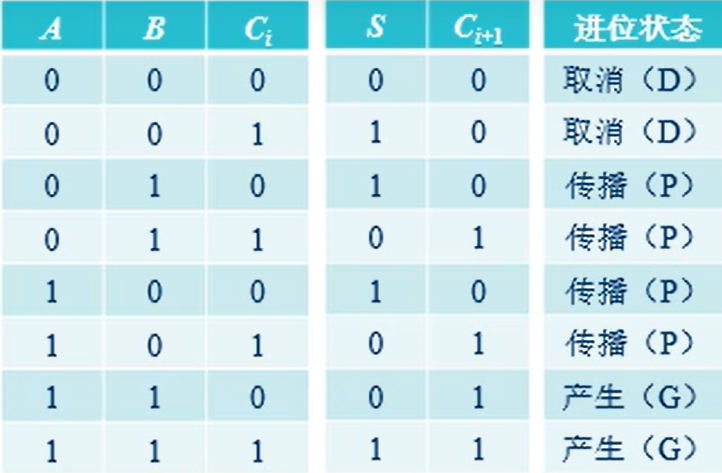
我们将全加器的进位分为如下三个状态。第一个状态称为进位取消状态，当A和B均为0时，无论Ci是0还是1都不会产生进位，即Ci+1等于0，进位取消状态用D表示，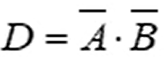
。第二个状态称为进位产生状态，当A和B都为1时，无论Ci是0还是1都会产生进位，即Ci+1等于1，进位产生状态用G表示，
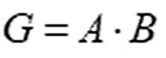。第三个状态时进位传播状态，当A和B有一个为1时，这时是否进位需要看上一级进位数Ci，此时Ci+1完全与Ci一样，进位传播状态用P表示，
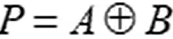。可以看出，D,G,P只与A和B有关，也就是说不需要上一级进位数Ci，在最早的时刻就可以得到进位状态。
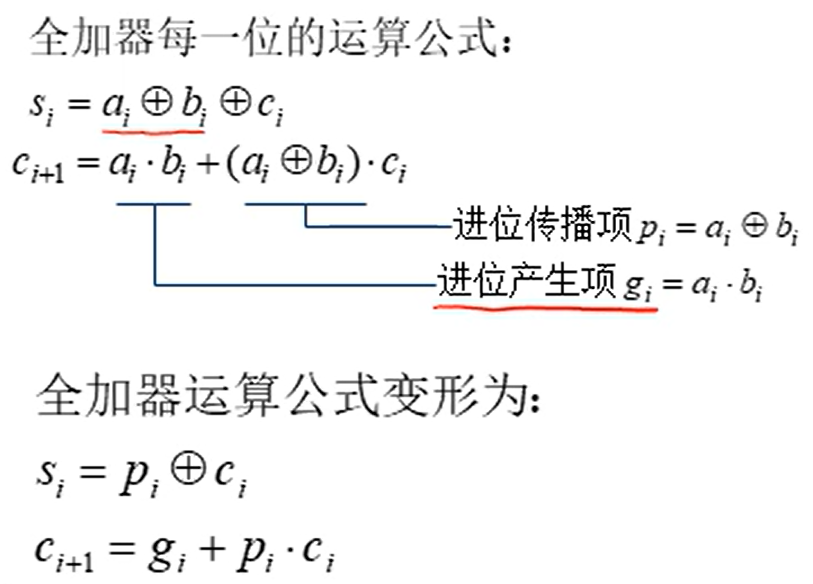
全加器的逻辑公式如下。Si本位数之前全加器已介绍。Ci+1下一级进位数可以这样理解，即当A和B都为1或者A和B有一个为1且Ci为1时需要进位(Ci+1=1)。我们要实现超前进位就要求解进位数C，C不仅与gi和pi有关还与上一级进位数Ci有关，同样根据此公式上一级进位数Ci又与上上级进位数Ci-1有关，依次推导。
以四位加法器为例，写出表达式如下
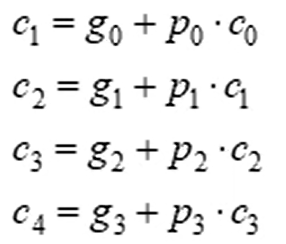
将C2,C3,C4依次带入C0，得
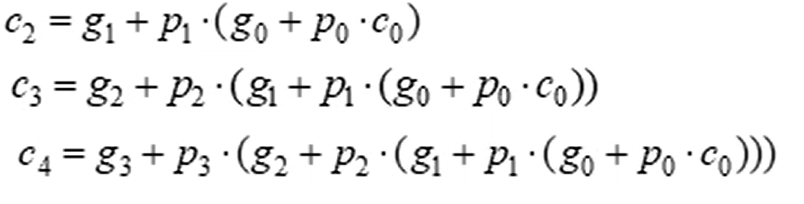
上式得g和p我们都可以根据ab求出。C0由A0和B0决定，这一位不存在上一级进位数，所以可以直接根据A0和B0求出C0。至此，所有的进位数C在一开始我们就可以同时求出。当前为s就可以根据公式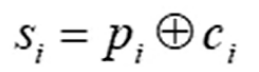
直接求出。
因此，超前进位加法器可以直接建立输入a0,a1,a2,a3,b0,b1,b2,b3到输出s0,s1,s2,s3,c0,c1,c2,c3得关系，不需要等待中间进位数c1,c2,c3的计算，因而速度更快，但同时电路会更复杂。
上述只是介绍了4位超前进位加法器就可以看到c4的式子已经很复杂了，那如果要是8位，16位，32位则式子会更加复杂，所需要的电路也会更加复杂。所以复杂到一定程度时超前进位电路运算所需的时间会大于逐位进位等待进位所需的时间，具体几位加法器才会导致这种问题这里不做说明。
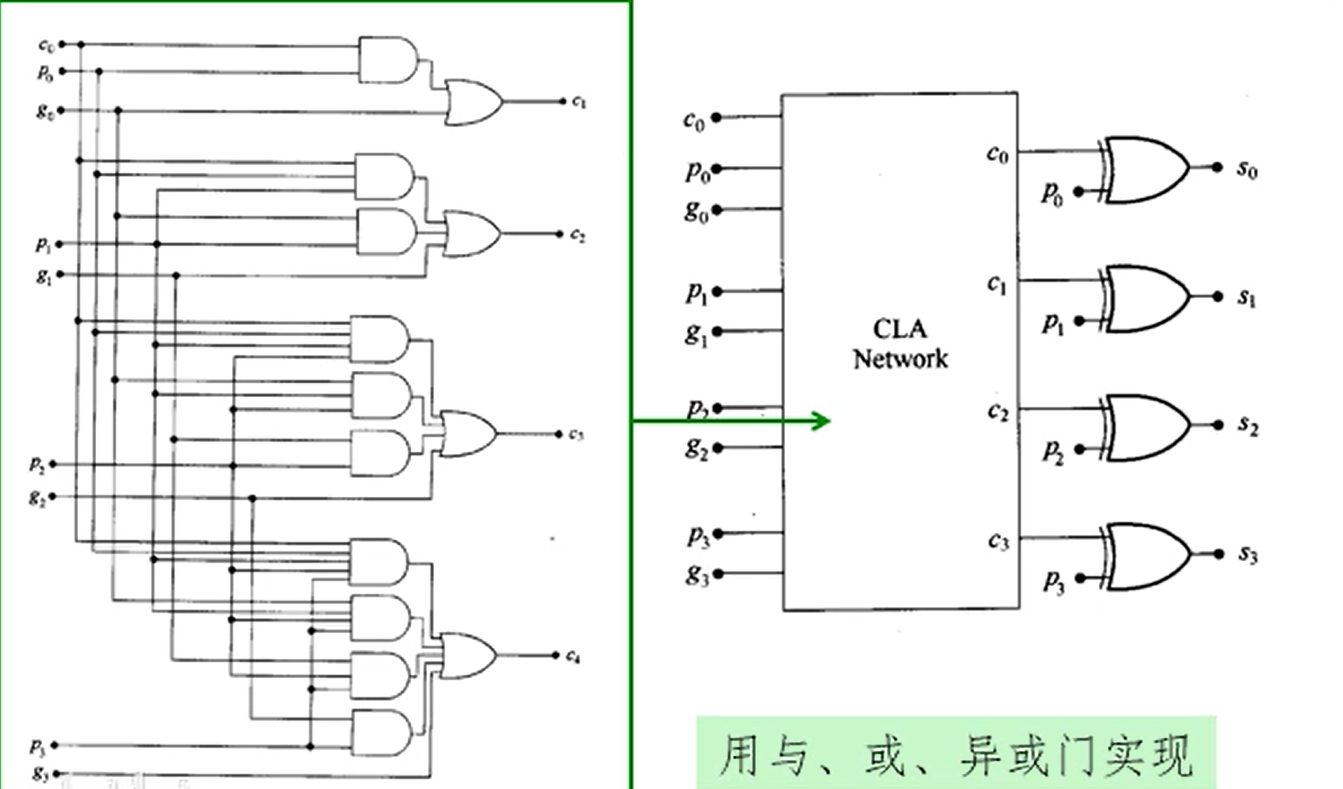
四位超前进位加法器电路图如图所示，随着加法器位数的增加可以看到它所需的门的数量也在增加。
时序逻辑电路
未完待续。。。