核心原理
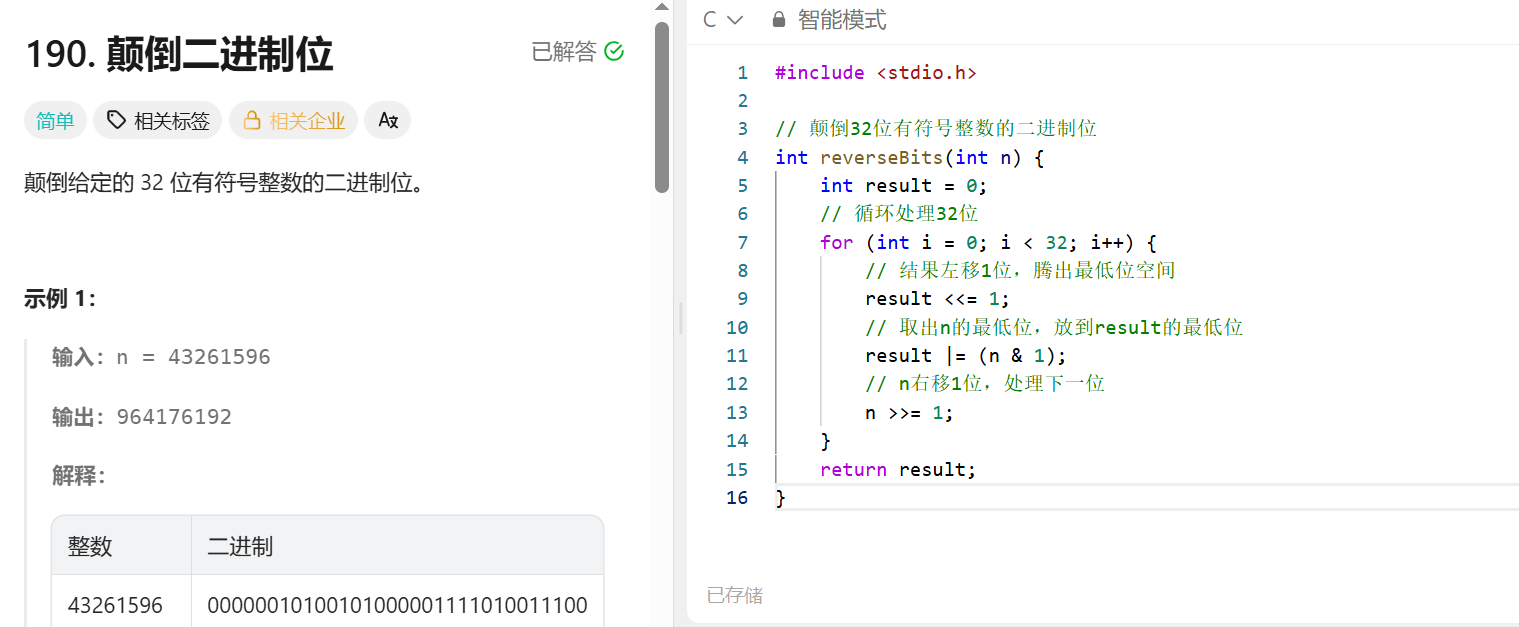
该方法的核心是逐位提取 + 反向填充:通过位运算逐位取出原数的二进制位(从最低位到最高位),同时将结果变量不断左移腾出空间,把提取的二进制位依次填充到结果的最低位,最终实现 32 位二进制位的整体颠倒。
方法优点
- 逻辑直观且易理解
整个过程完全贴合 "颠倒二进制位" 的字面语义,拆解为 "取位→移位→填位" 三个基础操作,步骤清晰,无复杂逻辑嵌套,新手也能快速理解核心思路,便于代码调试和维护。
- 时间复杂度最优(O (1))
固定循环 32 次(对应 32 位整数),循环次数与输入数值大小无关,属于常数级时间复杂度。无论输入是 0 还是 2³¹-2,执行次数始终为 32 次,在时间效率上达到理论最优。
- 空间复杂度最优(O (1))
仅使用一个临时变量result存储结果,未额外开辟数组、栈等数据结构,空间复杂度为常数级,内存占用极小,适合嵌入式、内存受限等场景。
- 位运算高效且无冗余
采用& 1(取最低位)、<<=(左移)、|=(填位)、>>=(右移)等基础位运算,这些操作由 CPU 直接支持,执行速度远快于算术运算或数据结构操作;
无多余的数值转换(如转字符串、转数组),避免了转换过程中的性能损耗和边界错误(比如字符串补零、数组越界)。
- 适配题目约束且鲁棒性强
针对题目中 "0 ≤ n ≤ 2³¹-2、n 为偶数" 的约束,无需额外处理负数符号位、奇数 / 偶数特殊逻辑,循环 32 次的设计确保原数高位的 0(如示例 1 中前 8 位的 0)也能被正确颠倒到低位,结果精准匹配 32 位整数的格式要求;
即使输入为边界值(如 2³¹-2),也能稳定输出正确结果,无溢出或逻辑漏洞。
- 可扩展性强
若需适配 64 位整数,仅需将循环次数改为 64 次,核心逻辑无需修改;
若需处理负数(补码形式),仅需在循环中保留符号位的处理逻辑,基础框架仍可复用。
总结
该方法以 "极简的逻辑、最优的时空复杂度、高效的位运算" 为核心优势,既满足题目场景的功能需求,又具备工程实现上的高性能和高鲁棒性,是解决 "固定长度二进制位颠倒" 问题的经典最优解法。