机器学习基础入门(第七篇)
神经网络训练优化与常见问题解析
一、前言
深度学习模型的 "智能" 不是来自模型结构本身,而是来源于训练过程中的学习 。换句话说,一个网络能否学会识别、理解或预测,关键取决于 ------如何定义损失函数、如何优化参数、如何避免陷入训练陷阱。
很多初学者训练神经网络时常会遇到:
-
模型收敛很慢;
-
损失函数不下降;
-
准确率波动剧烈;
-
训练集很好但测试集表现糟糕。
这些问题都源于训练优化的不当。本篇,我们将从原理、算法到实践,系统讲解神经网络训练优化的全过程。
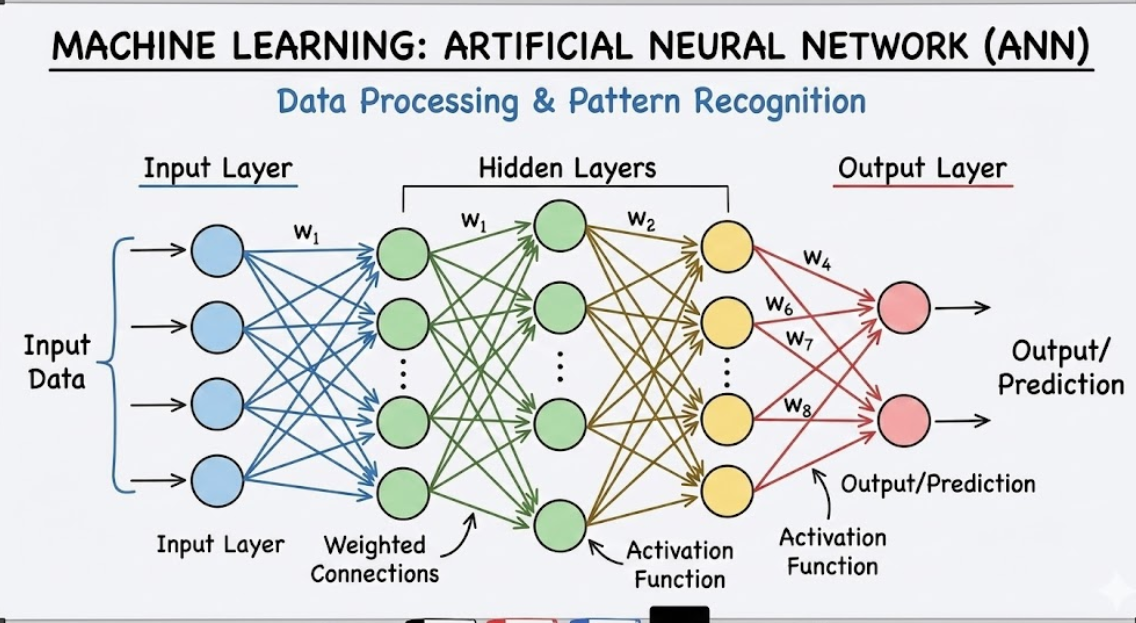
二、神经网络训练的基本原理
训练一个神经网络的目标是:让模型预测值 (y^\hat{y}y^) 尽可能接近真实标签 (yyy)。
为了衡量两者之间的差距,我们定义损失函数(Loss Function):
L=1N∑iℓ(yi,yi^)L = \frac{1}{N} \sum_i \ell(y_i, \hat{y_i})L=N1∑iℓ(yi,yi^)
其中 ℓ\ellℓ 表示样本的误差度量,NNN 为样本数量。通过最小化损失函数,神经网络不断调整权重参数。
整个训练流程可以概括为三个阶段:
-
前向传播(Forward Propagation):输入 → 输出,计算预测值;
-
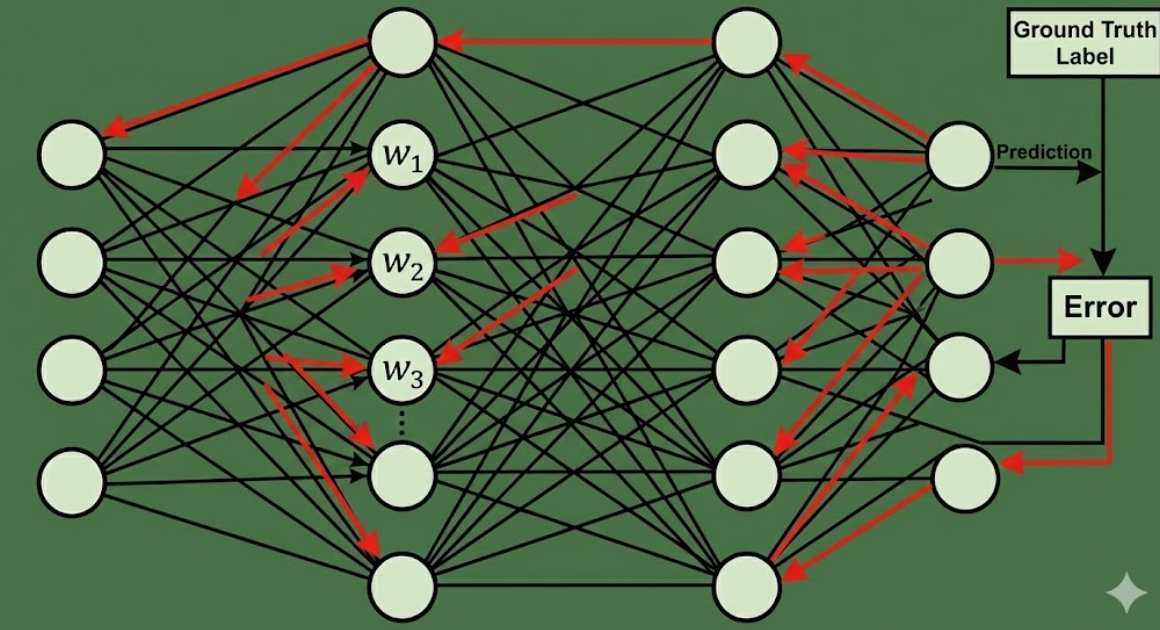
反向传播(Backpropagation):计算梯度,确定参数方向;
-
参数更新(Optimization Step):根据梯度调整权重。
三、损失函数(Loss Function)
损失函数是训练的 "指南针",它定义了什么是 "好" 的模型。不同任务选择不同的损失函数。
1. 回归任务常用损失函数
| 名称 | 公式 | 特点 |
|---|---|---|
| 均方误差 (MSE) | L=1N∑(y−y^)2L = \frac{1}{N}\sum (y - \hat{y})^2L=N1∑(y−y^)2 | 对大误差敏感,常用于回归 |
| 平均绝对误差 (MAE) | $L = \frac{1}{N}\sum | y - \hat{y} |
| Huber 损失 | 结合 MSE 与 MAE 的优点 | 对异常值更稳健 |
2. 分类任务常用损失函数
| 名称 | 公式 | 说明 |
|---|---|---|
| 交叉熵损失 (Cross-Entropy) | L=−∑yilog(yi^)L = -\sum y_i \log(\hat{y_i})L=−∑yilog(yi^) | 最常用的分类损失 |
| 二分类 BCE | L=−[ylog(p)+(1−y)log(1−p)]L = -[y\log(p)+(1-y)\log(1-p)]L=−[ylog(p)+(1−y)log(1−p)] | 对应 Sigmoid 输出 |
| 多分类 CE | L=−∑yilog(Softmax(zi))L = -\sum y_i\log(\text{Softmax}(z_i))L=−∑yilog(Softmax(zi)) | 对应 Softmax 输出 |
💡
直观理解:
交叉熵衡量两个概率分布的差异。如果预测分布与真实分布越接近,交叉熵损失越小。
四、优化算法(Optimizer)
优化算法决定了网络如何根据梯度更新参数,是训练的 "引擎"。
1. 梯度下降法(Gradient Descent)
最基本的优化算法:
w←w−η∂L∂ww \leftarrow w - \eta \frac{\partial L}{\partial w}w←w−η∂w∂L
其中 η\etaη 是学习率(learning rate)。梯度下降可以分为三种:
| 类型 | 特点 |
|---|---|
| 批量梯度下降(BGD) | 使用全部样本计算梯度,稳定但慢 |
| 随机梯度下降(SGD) | 每次更新用一个样本,快但波动大 |
| 小批量梯度下降(Mini-batch SGD) | 折中方案,是主流方法 |
2. 学习率的重要性
学习率 η\etaη 决定了每次更新的 "步长":
-
太小 → 收敛慢;
-
太大 → 可能震荡甚至发散。
现代深度学习常使用动态学习率(如学习率衰减、余弦退火、Warmup)来提升训练稳定性。
3. 动量优化(Momentum)
为了解决 SGD 的 "震荡" 问题,引入动量项,让参数更新带有惯性:
vt=βvt−1+(1−β)∇Lv_t = \beta v_{t-1} + (1-\beta)\nabla Lvt=βvt−1+(1−β)∇L
w←w−ηvtw \leftarrow w - \eta v_tw←w−ηvt
这样可以在梯度方向上加速收敛,减少局部振荡。
4. RMSProp、Adam 等自适应优化算法
这些算法可以自动调整每个参数的学习率。
| 算法 | 特点 |
|---|---|
| RMSProp | 适应不同梯度尺度,常用于 RNN |
| Adam | 结合 Momentum 与 RMSProp,几乎是默认选择 |
| AdamW | 改进版 Adam,增加权重衰减防止过拟合 |
| Adagrad | 对频繁更新的参数减小学习率 |
Adam 的更新公式如下:
mt=β1mt−1+(1−β1)gtm_t = \beta_1 m_{t-1} + (1 - \beta_1) g_tmt=β1mt−1+(1−β1)gt
vt=β2vt−1+(1−β2)gt2v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2vt=β2vt−1+(1−β2)gt2
w←w−ηmtvt+ϵw \leftarrow w - \eta \frac{m_t}{\sqrt{v_t} + \epsilon}w←w−ηvt +ϵmt
它能自动适应不同维度的梯度变化,使训练更加高效。
五、神经网络训练中的常见问题
尽管理论完备,但在实践中仍然会遇到各种问题。我们来系统分析最常见的几个:
1. 梯度消失与梯度爆炸
当神经网络层数较多时,梯度在反向传播过程中会不断累积或衰减。导致:
-
梯度趋近于 0 → 参数无法更新(梯度消失);
-
梯度过大 → 参数发散(梯度爆炸)。
解决方案:
✅ 使用合适的激活函数(ReLU 代替 Sigmoid/Tanh)
✅ 采用 Batch Normalization 稳定分布
✅ 使用合理的权重初始化(如 Xavier、He 初始化)
✅ 对梯度进行裁剪(Gradient Clipping)
✅ 使用残差结构(ResNet)减少梯度传递距离
2. 过拟合(Overfitting)
表现: 训练集准确率高,但测试集准确率低。模型过度记忆训练样本,泛化能力差。
解决方案:
✅ 数据层面:
-
数据增强(Data Augmentation)
-
扩充训练集
✅ 模型层面:
-
Dropout(随机失活部分神经元)
-
L1/L2 正则化(约束权重大小)
-
提前停止(Early Stopping)
✅ 优化层面:
-
使用权重衰减(Weight Decay)
-
使用更简单的模型结构
💡 深度学习的成功关键之一,是学会
在复杂模型与泛化能力之间取得平衡
。
3. 欠拟合(Underfitting)
表现: 模型在训练集上效果就不好,说明它 "学得太少"。原因可能是模型容量不足或特征表达能力弱。
解决方案:
✅ 增加模型复杂度(更多层或神经元)
✅ 延长训练轮数
✅ 减少正则化力度
✅ 选择更合适的特征表示
4. 学习率不合适
学习率太大会导致训练震荡、损失不收敛;太小则训练缓慢。
解决方案:
✅ 使用学习率衰减(LR Decay)
✅ 采用自适应学习率优化器(Adam、RMSProp)
✅ 使用余弦退火(Cosine Annealing)或循环学习率(Cyclic LR)
5. 数据分布不均 / 批量不稳定
神经网络极度依赖数据的统计特性,如果输入分布变化,训练会变得不稳定。
解决方案:
✅ 使用 Batch Normalization(BN):对每一层输入做归一化,保持数值稳定,加速收敛。
✅ 使用 Layer Normalization / Group Normalization:在 RNN 或 Transformer 中更常见。
6. 参数初始化问题
如果初始参数太小,梯度会快速消失;太大则会爆炸。
解决方案:
✅ Xavier 初始化(适合 Sigmoid/Tanh)
✅ He 初始化(适合 ReLU)
这两种初始化方法保证了前后层方差一致,避免梯度衰减或放大。
六、提高训练效率的技巧
在大规模深度学习训练中,效率优化同样关键:
1. Mini-batch 训练
将数据分成小批次(如 32、64、128),平衡计算效率与梯度稳定性。
2. 批量归一化(Batch Normalization)
标准化每层输入,使激活值分布更加稳定,能显著提高训练速度。
3. 学习率调度(Learning Rate Scheduler)
动态调整学习率,比如:
-
StepLR:每隔若干 epoch 下降;
-
Cosine Annealing:周期性下降;
-
Warmup:初期逐渐增大学习率以避免不稳定。
4. 正则化与 Dropout
Dropout 在训练时随机丢弃神经元,防止过拟合。通常丢弃率设置为 0.3--0.5 之间效果较好。
5. 提前停止(Early Stopping)
当验证集损失在若干轮后不再下降时,提前结束训练。
七、PyTorch 实践示例
下面给出一个简化的神经网络训练流程示例(用于分类任务):
import torch
import torch.nn as nn
import torch.optim as optim
# ==========================================
# 第一步:准备数据 (Data Preparation)
# ==========================================
# 假设有 100 个样本,每个样本有 10 个特征(比如身高、体重、毛色等)
# 目标是将其分为 2 类(0 或 1,比如 猫 或 狗)
input_data = torch.randn(100, 10) # 输入数据 (Batch Size=100, Features=10)
labels = torch.randint(0, 2, (100,)) # 真实标签 (0或1)
# ==========================================
# 第二步:搭建模型 (Build Model)
# ==========================================
# 一个简单的两层神经网络
class SimpleNet(nn.Module):
def __init__(self):
super(SimpleNet, self).__init__()
# 层1:输入10个特征 -> 输出5个隐藏特征
self.layer1 = nn.Linear(10, 5)
# 层2:输入5个特征 -> 输出2个类别分数
self.layer2 = nn.Linear(5, 2)
# 激活函数:增加非线性(相当于让模型学会思考,不仅仅是死算)
self.relu = nn.ReLU()
def forward(self, x):
x = self.layer1(x)
x = self.relu(x)
x = self.layer2(x)
return x
model = SimpleNet()
# ==========================================
# 第三步:定义"裁判"和"教练" (Loss & Optimizer)
# ==========================================
# 损失函数 (Loss):衡量猜得有多烂 (交叉熵损失常用于分类)
criterion = nn.CrossEntropyLoss()
# 优化器 (Optimizer):负责更新参数 (SGD 是随机梯度下降)
# lr=0.01 是学习率,相当于小孩学习的步子大小
optimizer = optim.SGD(model.parameters(), lr=0.01)
# ==========================================
# 第四步:训练循环 (Training Loop)
# ==========================================
epochs = 100 # 训练 100 轮
for epoch in range(epochs):
# 1. 前向传播:模型进行预测
outputs = model(input_data)
# 2. 计算损失:比较预测结果和真实标签
loss = criterion(outputs, labels)
# 3. 梯度清零:清除上一轮的梯度(PyTorch特性,防止梯度累加)
optimizer.zero_grad()
# 4. 反向传播:计算每个参数对误差的贡献(梯度)
loss.backward()
# 5. 更新参数:根据梯度调整权重
optimizer.step()
# 每10轮打印一次进度
if (epoch+1) % 10 == 0:
print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')
print("训练完成!")✅ 这段代码演示了前向传播、反向传播与参数更新的全过程,适合作为入门模板。
八、总结
神经网络的训练优化是一门 "艺术与科学的结合"。它涉及数学理论(梯度下降、损失函数)、算法策略(优化器、正则化)、以及经验技巧(学习率、归一化、提前停止)。
要想训练出性能优异、泛化良好的模型,你需要不断:
-
观察曲线变化;
-
调整超参数;
-
理解每一个 "优化手段" 的作用机制。
深度学习不仅仅是堆层数,更重要的是如何让模型 "稳定地学会"。