基于非线性全变分噪声去除算法的TV去噪模型算法图像去噪重构Matlab源代码及详细注释

基于非线性全变分噪声去除算法 TV去噪模型算法图像去噪重构 matlab源代码代码有详细注释，完美运行

全变分去噪这玩意儿在图像处理圈混了二十多年依然坚挺，核心就一句话：好的图像应该光滑但保留边缘。传统的高斯滤波把图像当软柿子捏，结果边缘糊成一团。TV模型鸡贼地改用全变分当正则项，边降噪边护住边缘，今天咱们用Matlab代码拆解它的暴力美学。

先看主函数骨架：

matlab 复制代码

function u = tv_denoise(f, lambda, max_iter)
    % 输入参数
    % f: 含噪图像（归一化到[0,1]）
    % lambda: 保真项权重（建议0.02~0.15）
    % max_iter: 最大迭代次数（通常200~500）
    
    u = f; % 初始化
    tau = 0.25; % 时间步长（别超过0.25）
    for k = 1:max_iter
        [ux, uy] = gradient(u);
        grad = sqrt(ux.^2 + uy.^2 + 1e-3); % 加小常数防除零
        u = u + tau*(divergence(ux./grad, uy./grad) - lambda*(u - f));
        % 显示迭代进度
        if mod(k,50)==0
            fprintf('Iter %d, diff:%.4f\n',k,norm(u-f));
        end
    end
end

这段代码里梯度计算和散度计算是灵魂操作。Matlab内置的gradient函数返回横向纵向梯度，但要注意它的边界处理是镜像对称的。后面的divergence需要自己实现：

matlab 复制代码

function d = divergence(a,b)
    % 散度计算（梯度算子的负共轭）
    d = [a(:,end,:) - a(:, 1,:), -diff(a,1,2)];
    d = d + [b(end,:,:) - b(1,:,:); -diff(b,1,1)];
end

这里有个坑：梯度算子和散度算子必须严格互逆。如果用前向差分算梯度，散度就得用后向差分，这样能量才能稳定下降。

迭代过程中的tau参数控制更新步长，超过0.25容易炸。lambda的调参技巧：噪声大时适当减小，想保留更多细节则增大。实际跑代码时建议先对图像做归一化，否则参数调整会想杀人。

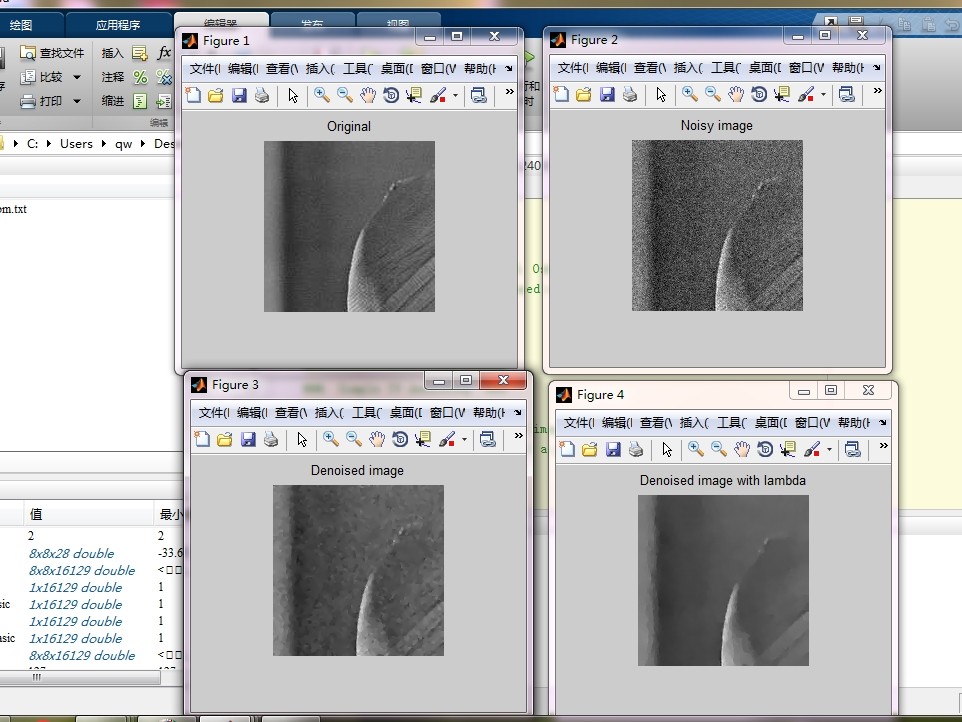
看看处理效果对比（假设f是读入的噪声图像）：

matlab 复制代码

% 预处理
f = im2double(imread('noisy_img.jpg'));
% 执行去噪
clean_img = tv_denoise(f, 0.1, 300);
% 效果对比
imshowpair(f, clean_img, 'montage');

运行后能看到噪声明显减少，但物体边缘依然犀利------这正是TV模型的看家本领。不过要注意，对于纹理丰富的区域可能会出现过平滑，这时候需要结合非局部均值之类的招数来补刀。

最后说个实战技巧：在迭代中监控能量函数变化，如果发现震荡就赶紧减小tau。TV模型虽然简单，但调参得当的话，效果能吊打不少深度学习模型，特别是在计算资源受限的场合。代码扔到GPU上加速的话，处理速度直接起飞，毕竟核心就是些矩阵运算。