相向双指针—接雨水

相向双指针

1、盛最多水的容器
- [1.1 题目描述](#1.1 题目描述)
- [1.2 解答思路](#1.2 解答思路)
2、接雨水
- [2.1 题目描述](#2.1 题目描述)
- [2.2 解答思路](#2.2 解答思路)
- - [2.2.1 前后缀分解](#2.2.1 前后缀分解)
  - [2.2.2 相向双指针](#2.2.2 相向双指针)

1、盛最多水的容器

1.1 题目描述

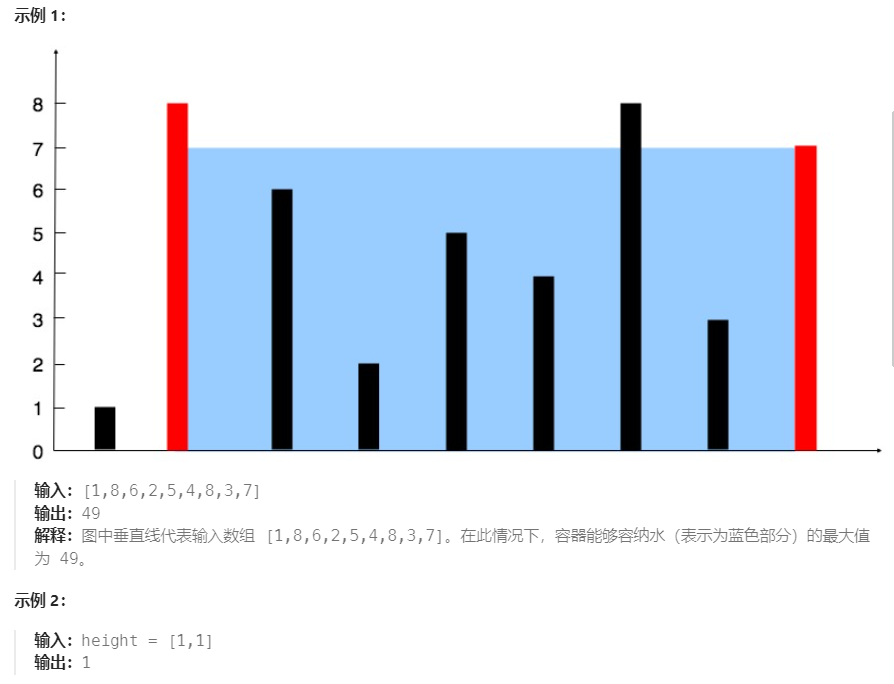
1.2 解答思路

我们可以举例子思考：如果有两条线，高度分别是7和8，宽度是5，那么容纳的水的容量就是7乘以5=35，易知高度是由较短的那条线决定的。此时如果我们保持高度为7的线不变，将宽度变小，试图找到容纳更多的水的两条线，那么不管新找到的线的高度比7大还是小，面积都不会比之前的7和8组成的容器能容纳的水量更大 ，因为如果线比7高，面积仍然由高度为7的线决定，如果线比7低，面积就会更小，因此此时我们就需要舍弃7那条线 ，以高度为8的那条线为容器的边来考虑新的可能，（这样8更小的宽度才有可能大于7 5），之后会继续比较8和新的线，从而舍弃更低的来找到可以储存最大水量的容器。

根据上述分析，我们就可以分别将左右指针指向数组的左右两边，计算能容纳的水量后，比较左右指针所指的数的大小，舍弃更小的那个数，即左指针右移或者右指针左移，从而可能在宽度变小的情况下，由于高度变高而能够容纳更多的水量。

python 复制代码

class Solution:
    def maxArea(self, height: List[int]) -> int:
        n = len(height)
        ans = 0
        left = 0
        right = n-1

        while left < right:
            # 左指针所指的数更小，则舍弃更小的，即左指针右移
            if height[left] < height[right]:
                s = (right-left)*height[left]
                ans = max(ans, s)
                left += 1
            else:
                s = (right-left)*height[right]
                ans = max(ans, s)
                right -= 1

        return ans

可知，上述算法的时间复杂度是 O(n)，其中 n 是数组的长度；空间复杂度是 O(1)。

思路分析：

虽然这类问题的数组是无序的，但是我们仍然可以利用 O(1) 的时间舍弃一个数，即利用容器的面积由短板决定的性质。因此当左右指针相遇的时候，我们就已经探索了所有可能容纳更多水量的情况。
因为每次移动指针花费的时间是 O(1)，而左右指针移动花费的时间加起来是 O(n)，因此该算法的时间复杂度就是 O(n)。
因为算法中只用到了额外的几个变量，因此空间复杂度是 O(1)。

2、接雨水

2.1 题目描述

2.2 解答思路

2.2.1 前后缀分解

对于这道题我们一列列分析，将每一列看作是宽度为1的容器，两边存在两个木板来接雨水，能接雨水的量由两边木板的高度决定，那么两边木板的高度由什么决定呢？

对于第 i 列，左木板的高度由 i 左边所有柱子的最大高度所决定，右木板的高度由 i 右边所有柱子的最大高度决定，即最大前缀和最大后缀，因此我们只要算出每一列的左右木板高度，然后就可以利用最短木板长度*宽度1-当前柱子高度来计算接雨水量了。

这里需要两个数组分别来存储当前柱子的最大前缀和最大后缀，然后可以比较大小来计算接的的雨水量。

python 复制代码

class Solution:
    def trap(self, height: List[int]) -> int:
        n = len(height)
        ans = 0

        # 得到各个柱子的最大前缀
        premax = [0]*n
        premax[0] = height[0]
        for i in range(1, n):
            premax[i] = max(height[i], premax[i-1])
        
        # 得到各个柱子的最大后缀
        sufmax = [0]*n
        sufmax[n-1] = height[n-1]
        for i in range(n-2,-1,-1):
            sufmax[i] = max(height[i], sufmax[i+1])

        # 计算接雨水量
        for h, pre, suf in zip(height, premax, sufmax):
             ans += min(pre, suf) - h

        return ans

可知，上述算法的时间复杂度是 O(n)，空间复杂度是 O(n)，其中 n 是柱子的数量。

思路分析：

首先需要把每个柱子看作是宽度为1的容器来考虑，然后需要分析当前柱子能接的雨水量是由什么决定的。

2.2.2 相向双指针

由于前后缀分解需要额外的数组，因此我们可以继续分析其他的性质：

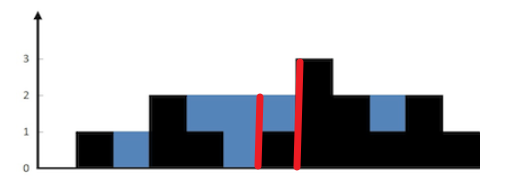
如果我们只知道左边一部分的最大前缀 1 和右边一部分的最大后缀 3，如图中黄色区域所示，那么对于第二个柱子，根据当前的最大前缀和最大后缀，我们可以知道左边木板的高度是1，而右边木板的高度至少是3。那么此时我们就可以知道第二个柱子的面积是由最大前缀，即高度为1的木板决定的，就可以得到当前柱子的接雨水量，对于右边部分的柱子也按此分析。

因此我们只需要两个相向双指针分别指向最左边和最右边，如果当前最大前缀小于最大后缀，那么就可以利用最大前缀来计算左指针对应的柱子的接水量；如果当前最大前缀大于最大后缀，那么就可以利用最大后缀来计算右指针对应的柱子的接水量；在指针移动的同时还要更新最大前缀和最大后缀。

python 复制代码

class Solution:
    def trap(self, height: List[int]) -> int:
        n = len(height)
        ans = 0
        left = 0
        right = n-1
        premax = 0
        sufmax = 0
        while left <= right:
            premax = max(premax, height[left])
            sufmax = max(sufmax, height[right])
            # 最大前缀更小的话，那么可以确定左指针所指的柱子的雨水量，左指针右移
            if premax < sufmax:
                ans += premax-height[left]
                left += 1
            # 最大后缀更小的话，那么可以确定右指针所指的柱子的雨水量，右指针左移
            else:
                ans += sufmax-height[right]
                right -= 1
            
        return ans

可知，上述算法的时间复杂度是 O(n)，空间复杂度是 O(1)，其中 n 是柱子的数量。

思路分析：

该算法的优化主要在于不需要遍历从而计算出确切的最大前缀和最大后缀，我们需要的是知道左右两个木板的大小关系（因为我们可以确切知道其中一个木板的高度，那么如果面积是由已知木板高度决定的，就可以直接计算面积），因此可以利用两个相向双指针分别指向最右边和最左边，对于指针指向的柱子，我们只能确定的知道其中一个木板的高度，另一个木板则根据当前的最大前缀或最大后缀从而得到两个木板的大小关系。如果已知的木板高度较小，那么就可以直接计算面积。