图机器学习（7）——图神经网络 (Graph Neural Network, GNN)

图机器学习（7）------图神经网络

- [0. 图神经网络](#0. 图神经网络)
- [1. 图神经网络原理](#1. 图神经网络原理)
- [2. GNN 变体](#2. GNN 变体)
- - [2.1 谱图卷积](#2.1 谱图卷积)
  - [2.2 空间图卷积](#2.2 空间图卷积)
- [3. 实现图卷积](#3. 实现图卷积)

0. 图神经网络

图神经网络 (Graph Neural Network, GNN) 是一类专门处理图结构数据的深度学习方法。这类方法也被称为几何深度学习 (geometric deep learning)，在社交网络分析、计算机图形学等众多领域正受到日益广泛的关注。

根据图机器学习中定义的分类法，GNN 的编码器部分同时接收图结构和节点特征作为输入。这类算法既可采用监督学习，也可采用无监督学习进行训练。本节我们将重点探讨无监督训练方式。

1. 图神经网络原理

卷积神经网络 (Convolutional Neural Network, CNN) 在处理规则欧几里得空间数据(如一维文本、二维图像、三维视频)时能取得卓越效果。典型 CNN 由多个层级组成，每一层都会提取多尺度的局部空间特征，深层网络则利用这些特征构建更复杂、表达能力更强的表征。

近年来研究发现，多层结构和局部性等概念同样适用于图结构数据的处理。然而，图数据定义在非欧几里得空间上，如何将 CNN 泛化到图结构并非易事，如下图所示：

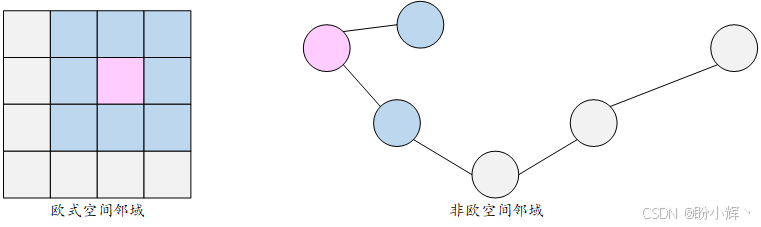
GNN 最初由 Scarselli 等于 2009 年提出。该方法的理论基础在于：每个节点都可以通过其特征和邻域信息来描述。来自邻域的信息(体现了图数据中的局部性概念)可以被聚合起来，用于计算更复杂的高层特征。接下来，我们详细解析其实现机制。

初始时，每个节点 v i v_i vi 都被赋予一个状态。为简化说明，我们暂时忽略节点属性，从随机嵌入 h i t h_i^t hit 开始。在算法的每次迭代中，节点会通过简单的神经网络层聚合来自邻居的信息：
h i t = ∑ v j ∈ N ( v i ) σ ( W h j t − 1 + b ) h_i^t = \sum_{v_j\in N(v_i)}\sigma (Wh^{t-1}_j + b) hit=vj∈N(vi)∑σ(Whjt−1+b)

其中， W ∈ R d × d W\in \mathbb R^{d\times d} W∈Rd×d 和 b ∈ R d b\in \mathbb R^d b∈Rd 是可训练的参数( d d d 是嵌入的维度)， σ \sigma σ 是一个非线性函数， t t t 代表算法的第 t t t 次迭代。该公式会递归执行，直到达到特定收敛条件。需要注意的是，每次迭代都会利用前次迭代计算得到的状态来计算新状态，这种状态传递机制与循环神经网络的工作原理相似。

2. GNN 变体

基于原始 GNN，研究人员提出了多种改进方案以优化图数据学习，增强其表征学习能力。其中部分变体专为处理特定类型的图结构设计(如有向/无向图、加权/无权图、静态/动态图等)。

在信息传播步骤方面，研究者提出了包括图卷积、门控机制、注意力机制和跳跃连接等在内的多种改进方案，旨在提升不同层级的表征能力。同时，各种创新的训练方法也不断涌现以优化学习效果。

在无监督表征学习领域，最常见的做法是采用编码器(通常为某种 GNN 变体)对图结构进行嵌入表示，再通过简单解码器重构邻接矩阵。其损失函数通常定义为原始邻接矩阵与重构矩阵的相似度：
Z = G N N ( X , A ) A ^ = Z Z T Z=GNN(X,A)\\ \hat A=ZZ^T Z=GNN(X,A)A^=ZZT

其中 A ∈ R d × d A\in \mathbb R^{d\times d} A∈Rd×d 为邻接矩阵， X ∈ R N × d X\in \mathbb R^{N\times d} X∈RN×d 为节点特征矩阵。另一种常见变体(尤其适用于图分类/表征学习任务)是采用目标距离训练策略：同时计算两个图的嵌入并获取联合表征，通过训练使该表征匹配预设的距离度量。类似策略也可应用于节点分类/表征学习，此时需采用节点相似度函数作为优化目标。

基于图卷积网络 (Graph Convolutional Network, GCN) 的编码器是无监督学习中最主流的 GNN 变体之一。GCN 模型借鉴了 CNN 的核心思想，其滤波器参数在整个图中共享，并通过堆叠多层结构构建深度网络。

图卷积操作主要分为两类：谱方法 (spectral approache) 和非谱(空间，spatial) 方法。谱方法在谱域定义卷积运算(即将图分解为简单元素的组合)；而空间方法则将卷积操作定义为对邻域特征的聚合运算。

2.1 谱图卷积

谱方法基于谱图理论，谱图理论研究图的特征与图关联矩阵的特征多项式、特征值和特征向量的关系。谱图卷积操作定义为信号(节点特征)与核的乘积。更具体地说，它通过图拉普拉斯矩阵(可视为特殊归一化的邻接矩阵)的特征分解在傅里叶域中实现。

虽然这种谱卷积定义具有坚实的数学基础，但其计算复杂度极高。为此，研究者提出了多种高效近似方法。例如 Defferrard 等人提出的 ChebNet，通过使用 K 阶切比雪夫多项式(切比雪夫多项式是一种用于高效逼近函数的特殊多项式)的概念来近似该操作。

其中，参数 K 决定了滤波器的局部性范围。直观地讲，K=1 时，仅考虑节点自身特征及其直接相连的一阶邻居；对于 K=2 时，聚合两跳邻居(邻居的邻居)特征，以此类推。

设节点特征矩阵为 X ∈ R N × d X∈\mathbb R^{N×d} X∈RN×d。传统神经网络层的计算形式为：
H l = σ ( X W ) H^l=σ(XW) Hl=σ(XW)

其中 W ∈ R N × N W\in \mathbb R^{N\times N} W∈RN×N 为权重矩阵， σ σ σ 为非线性激活函数。但此操作独立处理各节点信号，忽略了节点之间的连接。改进方法通过引入邻接矩阵 A ∈ R N × N A∈\mathbb R^{N×N} A∈RN×N ，为每个节点及其对应的邻居添加了一个新的线性组合，实现邻域信息聚合：
H l = σ ( A X W ) H^l=σ(AXW) Hl=σ(AXW)

该式使节点表征取决于其邻域特征，且所有节点共享相同的参数矩阵 W W W，实现高效并行计算。

需要注意的是，该运算可以通过多次顺序重复执行来构建深度网络。在每一层，节点描述符 X X X 会被替换为前一层的输出 H l − 1 H^{l-1} Hl−1。

然而，前述公式存在一些局限性，不能直接应用。第一个局限是：通过乘以邻接矩阵 A A A，我们虽然考虑了节点的所有邻居特征，但却忽略了节点自身的特征。这个问题可以通过在图中添加自循环(即在邻接矩阵A上加上单位矩阵 I I I，得到 A ^ = A + I Â = A + I A^=A+I )来解决。

第二个局限与邻接矩阵本身有关。由于邻接矩阵通常未经归一化处理，我们会观察到高度数节点的特征值较大，而低度数节点的特征值较小。这将导致训练过程中出现诸多问题，因为优化算法通常对特征尺度很敏感。目前已提出多种对 A A A 进行归一化的方法。

例如，在 Kipf 和 Welling 提出的 GCN 模型中，通过将 A A A 与节点度数的对角矩阵 D D D 相乘实现归一化(使每行元素之和为 1： D − 1 A D^{-1}A D−1A)。具体而言，使用了对称归一化方法： D − 1 / 2 A D − 1 / 2 D^{-1/2}AD^{-1/2} D−1/2AD−1/2，从而得到以下传播规则：
H l = σ ( D ^ − 1 / 2 A ^ D ^ − 1 / 2 X W ) H^l = σ(\hat D^{-1/2}\hat A \hat D^{-1/2}XW) Hl=σ(D^−1/2A^D^−1/2XW)

其中， D ^ \hat D D^ 是 A ^ \hat A A^ 的对角节点度矩阵。

接下来，我们将按照 Kipf 和 Welling 的定义构建 GCN 模型，并应用该传播规则对 networkx 图进行嵌入表示。

(1) 首先，导入所需 Python 模块，使用 networkx 加载 Barbell 图：

python 复制代码

import networkx as nx
import numpy as np
G = nx.barbell_graph(m1=10,m2=4)

(2) 构建表示图 G G G 的邻接矩阵。由于该网络没有节点特征，我们将使用单位矩阵 I ∈ R N × N I∈\mathbb R^{N×N} I∈RN×N 作为节点特征：

python 复制代码

order = np.arange(G.number_of_nodes())
A = np.asmatrix(nx.to_numpy_array(G, nodelist=order))
I = np.eye(G.number_of_nodes())

(3) 接下来，添加自循环并准备对角节点度矩阵：

python 复制代码

A_hat = A + I
D_hat = np.array(np.sum(A_hat, axis=0))[0]
D_hat = np.array(np.diag(D_hat))
D_hat = np.linalg.inv(sqrtm(D_hat))
A_norm = D_hat @ A_hat @ D_hat

(4) 本节构建的 GCN 包含两个卷积层。定义层权重和传播规则。权重矩阵 W 采用 Glorot 均匀分布初始化，也可以使用其他初始化方法，例如高斯或均匀分布：

python 复制代码

def glorot_init(nin, nout):
  sd = np.sqrt(6.0 / (nin + nout))
  return np.random.uniform(-sd, sd, size=(nin, nout))

class GCNLayer():
  def __init__(self, n_inputs, n_outputs):
      self.n_inputs = n_inputs
      self.n_outputs = n_outputs
      self.W = glorot_init(self.n_outputs, self.n_inputs)
      self.activation = np.tanh
      
  def forward(self, A, X):
      self._X = (A @ X).T # (N,N)*(N,n_outputs) ==> (n_outputs,N)
      H = self.W @ self._X # (N, D)*(D, n_outputs) => (N, n_outputs)
      H = self.activation(H)
      return H.T # (n_outputs, N)

(5) 创建网络并执行前向传播，即通过网络传播信号：

python 复制代码

gcn1 = GCNLayer(G.number_of_nodes(), 8)
gcn2 = GCNLayer(8, 4)
gcn3 = GCNLayer(4, 2)
H1 = gcn1.forward(A_norm, I)
H2 = gcn2.forward(A_norm, H1)
H3 = gcn3.forward(A_norm, H2)

此时，H3 包含了通过 GCN 传播规则计算得到的嵌入表示。需要注意的是，我们选择输出维度为 2，这意味着嵌入是二维的，可以轻松可视化，如下所示：

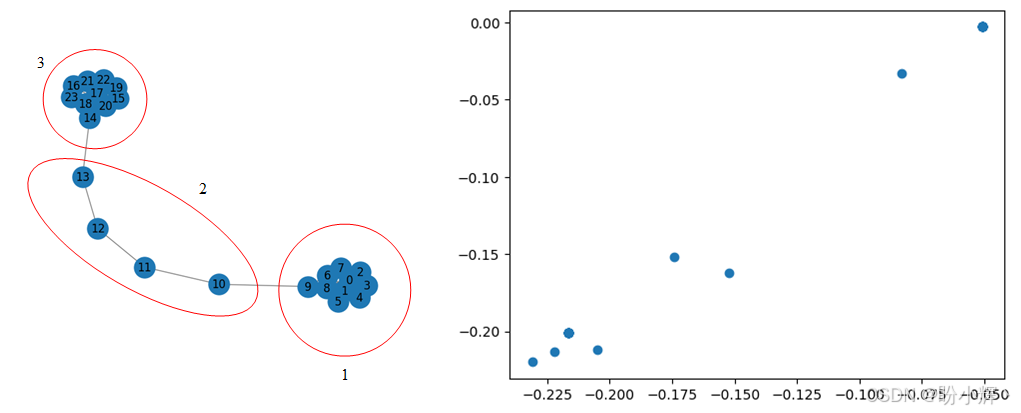
从结果中可以观察到两个明显分离的社区结构。考虑到我们尚未对网络进行训练，这已经是一个相当不错的结果。

谱图卷积方法已在多个领域取得显著成果，但仍存在一些局限性。例如，当处理包含数十亿节点的大型图时，谱方法要求同时处理整个图结构，这在计算上是不可行的。此外，谱卷积通常假设图结构固定，导致其在新图数据上的泛化能力较差。为了解决这些问题，空间图卷积提出了一种不同的方案。

2.2 空间图卷积

空间图卷积网络直接在图上操作，通过聚合空间邻近节点的信息进行计算。这种方法具有多重优势：权重可以在图的不同位置共享，从而在不同图上具有较好的泛化能力。此外，计算过程可以基于节点子集而非全图进行，显著提升计算效率。
GraphSAGE 是实现空间卷积的算法之一，主要特点是能够在各种类型的网络上进行扩展。该算法包含三个关键步骤：

邻域采样：对于图中的每个节点，第一步是找到它的 k 阶邻域，其中 k 需要自定义，用来决定考虑多少跳(邻居的邻居)
聚合：第二步是为每个节点聚合相应邻域的节点特征。可以使用各种类型的聚合，包括平均值聚合、池化聚合(按特定标准选取最优特征)或更复杂的运算，例如使用循环单元(如 LSTM)
预测：每个节点配备简易神经网络，基于聚合后的邻域特征进行预测。

GraphSAGE 通常用于监督学习环境，但通过采用相似度函数作为目标距离等策略，它也能有效支持无监督的嵌入学习任务，而无需显式监督任务。

3. 实现图卷积

GNN 可以在 TensorFlow、Keras 和 PyTorch 等主流深度学习框架中实现。接下来，我们使用 PyTorch 进行实现。

本节中，我们将以无监督的方式(无需目标变量)学习嵌入向量，基于成对图的联合嵌入学习，使嵌入距离匹配图的真实距离。

(1) 首先，加载所需模块：

python 复制代码

import os
import random
import numpy as np
import networkx as nx
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch_geometric.data import Data, Dataset, DataLoader
from torch_geometric.datasets import TUDataset
from torch_geometric.nn import GCNConv, global_mean_pool
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt

(2) 使用 PROTEINS 数据集，数据集包含 1114 个图，每个图平均有 39 个节点和 73 条边，每个节点具有 4 个特征向量：

python 复制代码

# PyG 自带的 TUDataset 会自动下载并处理好 PROTEINS
dataset = TUDataset(root="data/PROTEINS", name="PROTEINS")

# 查看数据集信息
print(f"Dataset: PROTEINS, graphs = {len(dataset)}, num_node_features = {dataset.num_node_features}")
print(dataset[0])

(3) 接下来，创建模型。该模型将由两个 GCN 层组成，输出维度分别为 64 和 32，并使用 ReLU 激活函数。输出计算为两个嵌入的欧几里得距离：

python 复制代码

class GCNEncoder(nn.Module):
    """
    GCNEncoder: 对单图做两层 GCN + 激活 + 全局平均池化，输出图嵌入。
    """
    def __init__(self, in_channels, hidden_channels, embedding_dim):
        super(GCNEncoder, self).__init__()
        # 第一层 GCN：in_channels -> hidden_channels
        self.conv1 = GCNConv(in_channels, hidden_channels)
        # 第二层 GCN：hidden_channels -> embedding_dim
        self.conv2 = GCNConv(hidden_channels, embedding_dim)

    def forward(self, x, edge_index, batch):
        """
        x: [N, in_channels]  节点特征
        edge_index: [2, E]   边列表
        batch: [N]          每个节点所属的图ID，用于全局池化
        """
        # 两层 GCN + ReLU
        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = self.conv2(x, edge_index)
        # 得到节点级别特征后，用 global_mean_pool 聚成图级别向量
        # 返回 shape = [num_graphs_in_batch, embedding_dim]
        x = global_mean_pool(x, batch)
        return x

(4) 准备数据集进行训练。对于每一对输入图，分配一个相似度分数。可以使用任何图相似度度量方法，如图编辑距离。为了简便起见，本节使用图的拉普拉斯矩阵谱距离作为相似度度量：

python 复制代码

class SiameseDistanceModel(nn.Module):
    """
    Siamese 模型：输入两张图的数据 (x1, edge_index1, batch1) 和 (x2, edge_index2, batch2)，
    用同一个 GCNEncoder 得到两个图的嵌入向量，然后计算它们的 L2 距离，输出一个回归值。
    """
    def __init__(self, gcn_encoder):
        super(SiameseDistanceModel, self).__init__()
        self.encoder = gcn_encoder

    def forward(self, data1, data2):
        """
        data1, data2: 都是 PyG Data 或者包含 (x, edge_index, batch) 的对象
        返回：
            dist: [batch_size] 的张量，表示两张图嵌入后的 L2 距离
        """
        # 分别对两组图做前向
        z1 = self.encoder(data1.x, data1.edge_index, data1.batch)
        z2 = self.encoder(data2.x, data2.edge_index, data2.batch)
        # 计算 L2 距离：norm along 1 维
        dist = torch.norm(z1 - z2, p=2, dim=1)
        return dist

def graph_spectrum_distance(pyg_data1, pyg_data2, max_k=100):
    """
    使用 networkx 计算拉普拉斯矩阵的特征值谱，然后做 L2 距离
    """
    # 将 PyG Data 转成 networkx 图（无特征）
    # pyg_data.edge_index 是 2 x E 的 LongTensor
    edge_numpy = pyg_data1.edge_index.cpu().numpy()
    G1 = nx.Graph()
    # 添加节点
    G1.add_nodes_from(range(pyg_data1.num_nodes))
    # 添加边
    edges1 = list(zip(edge_numpy[0], edge_numpy[1]))
    G1.add_edges_from(edges1)

    edge_numpy2 = pyg_data2.edge_index.cpu().numpy()
    G2 = nx.Graph()
    G2.add_nodes_from(range(pyg_data2.num_nodes))
    edges2 = list(zip(edge_numpy2[0], edge_numpy2[1]))
    G2.add_edges_from(edges2)

    # 计算拉普拉斯特征值谱（返回 numpy 数组，升序）
    spec1 = np.linalg.eigvalsh(nx.laplacian_matrix(G1).todense())
    spec2 = np.linalg.eigvalsh(nx.laplacian_matrix(G2).todense())

    # 截断到相同长度
    k = min(len(spec1), len(spec2), max_k)
    v1 = np.sort(spec1)[:k]
    v2 = np.sort(spec2)[:k]

    return np.linalg.norm(v1 - v2)

class PairDataset(Dataset):
    """
    自定义 PyG Dataset，用于存储 图 对 (i, j) 以及它们对应的 target 距离。
    内部直接持有一个列表：[(idx1, idx2, target_distance), ...]，
    __getitem__ 返回两个图的 Data 对象以及这个距离。
    """

    def __init__(self, base_dataset, pairs):
        """
        base_dataset:         PyG 的图集合（例如前面加载的 PROTEINS TUDataset）
        pairs: List of tuples  (i, j, target_ij)
        """
        super(PairDataset, self).__init__()
        self.base_dataset = base_dataset
        self.pairs = pairs

    def len(self):
        return len(self.pairs)

    def get(self, idx):
        i, j, dist_ij = self.pairs[idx]
        data_i = self.base_dataset[i]
        data_j = self.base_dataset[j]
        return data_i, data_j, torch.tensor([dist_ij], dtype=torch.float32)

num_graphs = len(dataset)
num_pairs = 100  # 随机抽 100 对进行训练
pairs = []

pair_indices = np.random.randint(num_graphs, size=(num_pairs, 2))

print("开始计算每对图的谱距离...")
for (i, j) in pair_indices:
    d_ij = graph_spectrum_distance(dataset[i], dataset[j])
    pairs.append((int(i), int(j), float(d_ij)))
print("完成谱距离计算，总共", len(pairs), "对。")

# 构造 PairDataset
pair_dataset = PairDataset(dataset, pairs)

# 用 DataLoader 构建批次
def collate_pair(batch_list):
    """
    接收一个 batch_list: 例如 [(data1_i, data1_j, dist1), (data2_i, data2_j, dist2), ...]
    返回：
        batch_data_i, batch_data_j, targets_tensor
    """
    data_i_list = []
    data_j_list = []
    targets = []

    for (data_i, data_j, dist_val) in batch_list:
        data_i_list.append(data_i)
        data_j_list.append(data_j)
        targets.append(dist_val)

    # 使用 PyG 自带的 Batch.from_data_list
    from torch_geometric.data import Batch
    batch_i = Batch.from_data_list(data_i_list)
    batch_j = Batch.from_data_list(data_j_list)
    targets = torch.cat(targets, dim=0)  # [batch_size]

    return batch_i, batch_j, targets

# DataLoader
batch_size = 10
pair_loader = DataLoader(pair_dataset, batch_size=batch_size, shuffle=True, collate_fn=collate_pair)

(5) 最后，编译并训练模型。使用 Adam 优化器，并将学习率参数设为 1e-2，使用均方误差 (mean-square error, MSE) 作为损失函数(预测距离与真实谱距离的平方差)。模型训练 500 个 epoch：

python 复制代码

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print("使用设备：", device)

# 参数设置
in_channels = dataset.num_node_features  # PROTEINS 每个节点特征维度
hidden_channels = 64
embedding_dim = 32
lr = 1e-2
num_epochs = 500

# 实例化编码器 + SiameseDistanceModel
gcn_encoder = GCNEncoder(in_channels, hidden_channels, embedding_dim).to(device)
model = SiameseDistanceModel(gcn_encoder).to(device)

optimizer = torch.optim.Adam(model.parameters(), lr=lr)
criterion = nn.MSELoss()

# 训练记录
train_losses = []

print("开始训练...")
for epoch in range(1, num_epochs + 1):
    model.train()
    total_loss = 0.0

    for (batch_i, batch_j, targets) in pair_loader:
        batch_i = batch_i.to(device)
        batch_j = batch_j.to(device)
        targets = targets.to(device)  # [batch_size]

        optimizer.zero_grad()
        # forward
        preds = model(batch_i, batch_j)  # [batch_size]
        loss = criterion(preds, targets)
        loss.backward()
        optimizer.step()

        total_loss += loss.item() * targets.size(0)

    avg_loss = total_loss / len(pair_dataset)
    train_losses.append(avg_loss)

    if epoch % 50 == 0 or epoch == 1:
        print(f"Epoch {epoch:03d}/{num_epochs}  Loss: {avg_loss:.6f}")

print("训练结束！")

(6) 训练完成后，可以检查并可视化学习到的嵌入质量。由于输出是 32 维的，为了便于可视化，使用 t-SNE 降维至二维空间：

python 复制代码

# 先把整个 dataset 转成 DataLoader，这里每个 DataLoader 中只有单个图
all_loader = DataLoader(dataset, batch_size=64, shuffle=False)

model.eval()
embeddings = []
with torch.no_grad():
    for batch in all_loader:
        batch = batch.to(device)
        # batch.x, batch.edge_index, batch.batch
        z = gcn_encoder(batch.x, batch.edge_index, batch.batch)  # [batch_size, embedding_dim]
        embeddings.append(z.cpu().numpy())

embeddings = np.vstack(embeddings)  # [num_graphs, embedding_dim]
print("得到所有图的嵌入，shape =", embeddings.shape)

# 用 sklearn TSNE 降到 2 维
tsne = TSNE(n_components=2)
emb_2d = tsne.fit_transform(embeddings)

(7) 绘制嵌入。在图中，每个点(嵌入的图)根据其对应的标签进行着色(蓝色= 0，红色= 1)，结果如下图所示：

python 复制代码

# 准备颜色：用 dataset[i].y（原本的图标签）来着色
labels = np.array([int(d.y.item()) for d in dataset])  # PROTEINS 数据集有两个类别(0,1)，这里直接做 cat.codes

plt.figure(figsize=(12, 6))
scatter = plt.scatter(emb_2d[:, 0], emb_2d[:, 1], c=labels, cmap="jet", alpha=0.6)
plt.colorbar(scatter)
plt.title("TSNE of Graph Embeddings (PROTEINS)")
plt.show()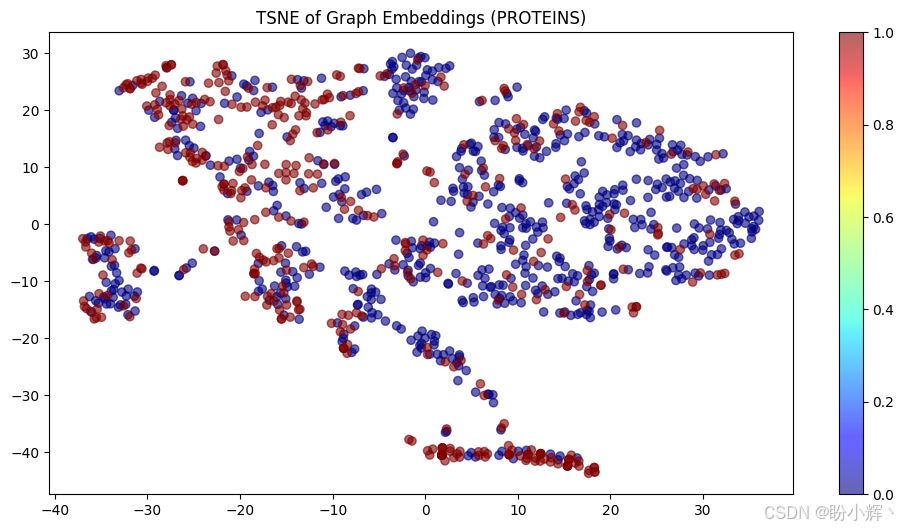

这只是图嵌入学习的众多方法之一，针对特定问题可以尝试更先进的解决方案。