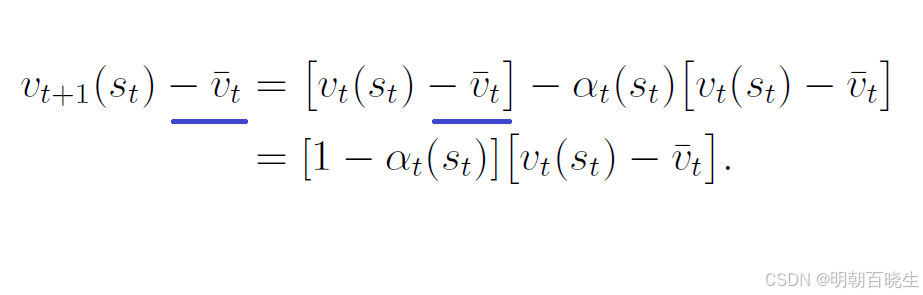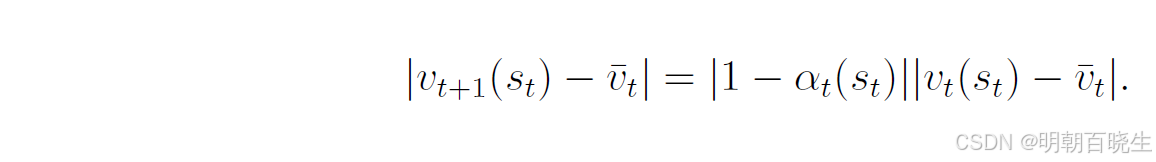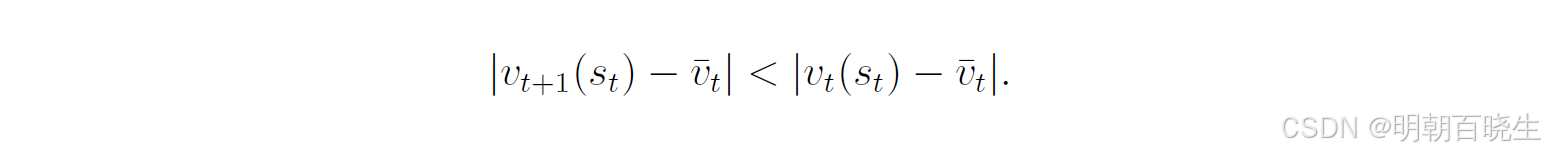强化学习[page13]【chapter7】时序差分方法算法介绍

时序差分学习通常泛指一大类强化学习算法。例如，本章介绍的所有算法都属于时序差分学习的范畴。但本节所讨论的时序差分学习特指一种用于估计状态值的经典算法。TD 方法的一个特点是，它在每个时间步更新其值估计，而 MC 方法则要等到回合结束才更新

TD 算法主要内容

• TD(0)：估计状态价值函数 (State-Value Function) V(s)。

• Sarsa：估计同轨策略动作价值函数 (On-policy Action-Value Function) Q(s, a)。

• Expected Sarsa：估计期望形式的动作价值函数 (Expected Action-Value Function)。

• n-step Sarsa：通过n步采样回报估计动作价值函数 Q(s, a)。

• Q-learning：直接估计最优动作价值函数 (Optimal Action-Value Function) Q*(s, a)

• 

---

目录：

1. Robbins-Monro(RM) 算法例子
2. TD(0） 算法描述
3. TD算法 性质分析

---

一 Robbins-Monro(RM) 算法例子

下面通过三个例子,介绍一下前面学习的RM算法和后面学习的Temporal-Dierence Methods联系

1.1 mean estimation

S代表随机变量,可观测的值为 idd samples

解:

转换为 root-finding problem

含噪声的实际测量值:

迭代公式为：

1.2 状态值

, 观测值 based on iid samples of S

解：

转换为 root-finding problem

实际样本测量值

(小写的s是实际采样的值）

迭代公式：

1.3 bellman 公式

,

观测值 based on iid samples of S

R,S are random variables, is a constant , is a function

obation of S,R

转换为 root-finding problem

实际样本测量值:

迭代公式：

---

二 TD(0） 算法描述

给定策略，我们的目标是估计所有状态对应的。假设我们拥有遵循策略π生成的经验样本，其中t表示时间步。以下时序差分算法可利用这些样本估计状态值：

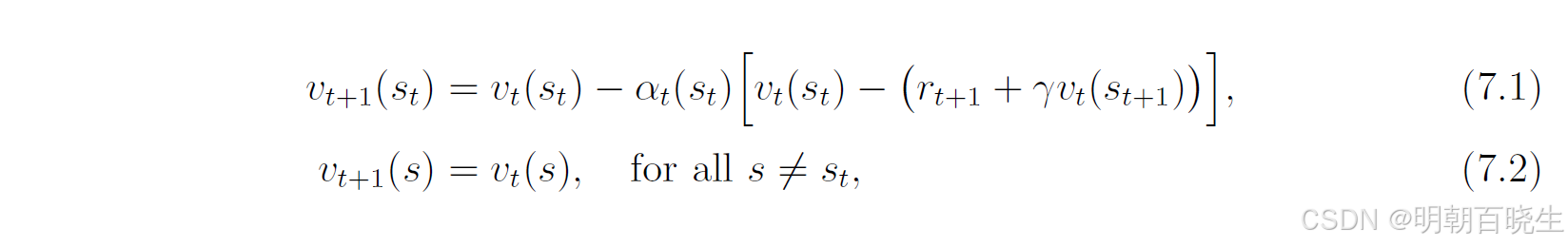
其中.这里表示t时刻按照策略对的估计值,表示t时刻状态对应的学习率。

需特别注意，在t时刻仅更新被访问状态的估值，如式(7.2)所示未访问状态的估值保持不变。为简洁起见，式(7.2)常被省略，但必须意识到若缺少该式，算法在数学上将不完整。

三 TD算法 性质分析

我们主要要理解两个问题

1. why is called TD target?
2. What is the interpretation of the TD error?

式(7.1)可描述为：

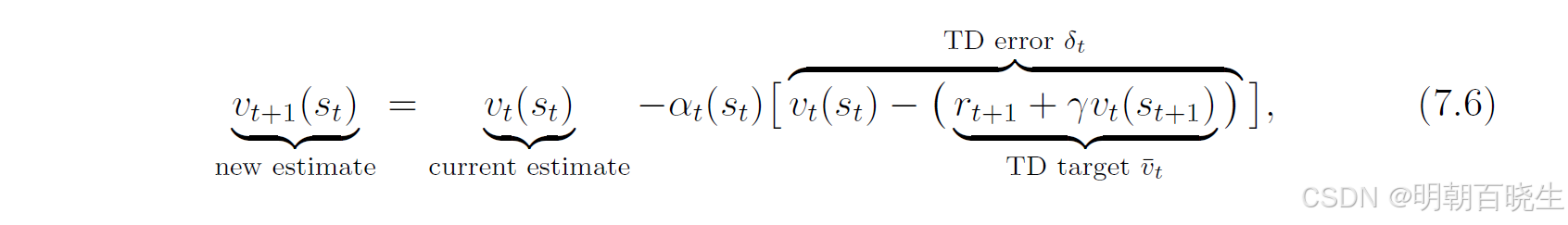
其中

TD target:

TD error

3.1 why is called TD target?

因为是算法试图驱使逼近的目标值。

将式(7.6)两边同时减去可得：

取等式两边的绝对值：

由于是较小的正数，有，因此：

该不等式具有重要意义，它表明新值比旧值 更加接近。这就是被称为TD目标值的原因。

2 What is the interpretation of the TD error?

首先，该误差之所以称为"时序差分"，是因为

反映了时间步t与t+1之间的差异。

其次，它反应了和之间的误差

当时，TD误差的期望值为：

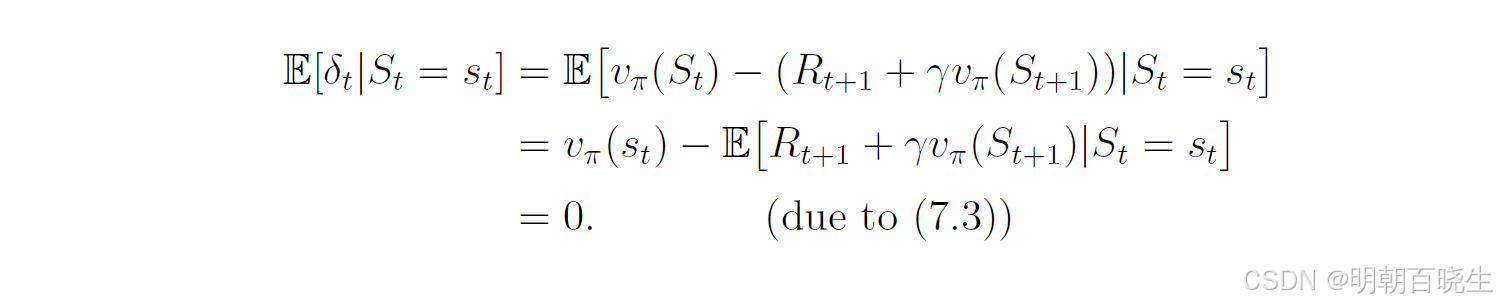
因此，TD误差不仅反映两个时间步之间的差异，更重要的是反映了估计值与真实状态值之间的差异。

3 innovation

TD误差可解释为innovation

表示从经验样本中获取的新信息。TD学习的核心思想是基于新获得的信息来修正当前对状态值的估计。innovation在许多估计问题（如卡尔曼滤波33,34）中都具有基础性地位。

其次，式(7.1)中的TD算法仅能估计给定策略的状态值。为寻找最优策略，我们仍需进一步计算动作值并进行策略改进，这将在7.2节介绍。尽管如此，本节介绍的TD算法非常基础，对理解本章其他算法至关重要。