单目标实数参数优化：算法jSO

Single Objective Real-Parameter Optimization: Algorithm jSO

摘要（Abstract）

解决单目标实数参数优化问题，亦称为边界约束优化，仍然是一项具有挑战性的任务。此类问题可见于工程优化、科学应用以及其他现实世界问题中。通常，这些问题非常复杂且计算成本高昂。本文提出了一种名为 jSO 的新算法。该算法是 iL-SHADE 算法的改进变体，主要改进在于采用了一种新的加权版本变异策略。实验在 CEC 2017 基准函数上进行，这些函数与先前竞赛的基准函数不同。首先，对提出的 jSO 算法与 L-SHADE 算法进行了比较。从所得结果可以得出结论，jSO 相较于 L-SHADE 算法表现更佳。其次，也对 jSO 和 iL-SHADE 进行了比较，jSO 取得了更好或具有竞争力的结果。使用 CEC 2017 的评估方法，jSO 在这三种算法中获得了最佳的最终得分。

I. 引言（INTRODUCTION）

单目标实数参数优化在各种研究中扮演着重要角色，越来越多的研究工作集中在解决复杂的优化问题上。已有多种算法被研究用于解决实数参数问题，其中，基于种群的算法因其易于用任何编程语言实现而显得非常有用。近年来，基于种群的算法主要可分为两类：进化算法（EAs）以及受自然启发的算法群（如蜜蜂、蚂蚁或免疫系统）。本文主要关注进化算法。

进化算法最大的缺点之一是种群多样性的丧失。其结果是，算法可能会过早地收敛于局部最优解。一个好的算法需要在进化过程的早期阶段保持足够高的种群多样性，而在后期阶段则需要降低种群多样性以提高收敛速度。

我们可以如下定义单目标全局优化（也称为边界约束优化）：对于一个目标函数 f(f(f(ec{x})$，算法需要找到向量 x⃗\vec{x}x 的变量值，以最小化/最大化 f(x⃗)f(\vec{x})f(x )。向量 x⃗={x1,x2,...,xD}\vec{x}=\{x_{1},x_{2},...,x_{D}\}x ={x1,x2,...,xD} 中的变量数量 DDD 表示问题的维度。搜索空间由变量的定义域决定，即由其下界 xj,lowx_{j,low}xj,low 和上界 xj,uppx_{j,upp}xj,upp 定义，其中 j=1,2,...,Dj=1,2,...,Dj=1,2,...,D。在黑盒优化中，任务是在没有目标函数形式或结构的明确知识的情况下解决全局优化问题，即 fff 是一个黑盒[1]。这类问题出现在工程优化、科学应用以及其他现实世界的优化问题中。

单目标优化可以包含在许多其他类型的优化中，如约束优化、多模态优化、多目标优化等。然而，每种类型的优化都面临一些挑战。在单目标优化中，函数 fff 可能有多个最优解，而算法需要找到全局最优解。如果算法将其种群困于局部最优解，优化的最终结果可能很差 。另一个挑战与优化问题的维度有关，因为当问题维度增加时，搜索空间会变得非常巨大。

差分进化（DE）算法[2]是一种用于数值优化的随机种群进化算法。DE算法实现简单。近几十年来，它展现了鲁棒性、高效性，并且在应用于解决现实世界优化问题时极具竞争力[3, 4]。DE特别适用于连续空间上的优化，此外，它也可用于离散域。

原始DE于1995年提出，至今许多研究已将原始算法或其改进变体应用于各种不同的领域。近期提出了大量改进方案[5]。

在本文中，我们提出了DE算法的一个新版本（jSO）。它类似于我们之前发表的iL-SHADE算法[7]，该算法在CEC 2016单目标实数参数优化竞赛中位列第三/第四。iL-SHADE算法是由Tanabe和Fukunaga提出的L-SHADE算法[6]的改进版本。

回顾实数参数单目标优化竞赛和/或专题会议的历史可知，CEC在2005年、2013年、2014年、2015年和2016年都曾组织过。CEC及其他会议也组织过密切相关的专题/竞赛，如大规模全局优化等。需要注意的是，CEC 2016和CEC 2017的基准函数是不同的，尽管两个竞赛中基准函数的数量相同。因此，我们可能无法直接比较本次与以往CEC竞赛所获得的结果。

本文的主要贡献如下：（1）提出了一种带有加权变异策略变体的新算法版本（jSO），（2）进行了CEC 2017竞赛的实验，（3）详细比较了jSO与L-SHADE算法，（4）对jSO、iL-SHADE和L-SHADE进行了总结性比较。

本文结构如下。第二部分给出了本工作的背景，包括DE的概述以及L-SHADE和iL-SHADE算法的描述。第三部分介绍了我们的新算法变体jSO，该算法用于本实验。第四部分展示了jSO算法在基准函数上的实验结果，并与L-SHADE和iL-SHADE进行了比较。第五部分以一些总结性评论结束全文。

II. 背景（BACKGROUND）

在本节中，我们将介绍差分进化（DE）及相关算法的一些背景知识。差分进化（DE）是一种基于种群的算法，属于进化算法类别。我们发现DE表现出优异的性能，并被应用于众多领域和研究之中[8, 9, 10, 11, 12, 13]。DE有三个需要用户在进化过程开始前设定的控制参数：FFF是缩放因子，CRCRCR是交叉控制参数，NPNPNP是种群大小。这些参数在原始DE算法中是固定的。虽然用户只需要设置三个参数，但要为它们找到合适的 值可能是一项耗时的工作。为了克服这个问题，已经提出了几种自适应和自适应的DE变体。在SADE[14]、jDE[15]、JADE[16]等算法中，控制参数FFF和CRCRCR是自适应的，因此用户无需设置和调整这两个控制参数，但仍需设置NPNPNP。通常，NPNPNP在优化过程中保持不变。最近，已经有一些尝试在进化过程中调整此控制参数[6, 17]。

SHADE[1]是一种基于DE的算法，它使用基于成功历史的参数自适应机制来调整CRCRCR和FFF。线性种群规模缩减（LPSR）被应用于SHADE中，该机制根据线性函数持续减少种群大小，得到的算法称为L-SHADE[6]。SHADE和L-SHADE算法启发了许多研究。L-SHADE的改进版本在CEC 2015竞赛中名列前茅：SPS-L-SHADE-EIG[18]、DESPA[19]、LSHADE-ND[20]；在CEC 2016竞赛中亦然：LSHADE_EpSin[21]（将集成正弦参数自适应与L-SHADE结合）、LSHADE44[22]（采用竞争策略的L-SHADE）以及iL-SHADE[7]。

A. 差分进化（Differential Evolution）

DE算法[2]是一种基于种群的算法。其种群(P)由(NP)个向量组成：

Pg=(x⃗1,g,...,x⃗i,g,...,x⃗NP,g), i=1,2,...,NP,\mathbf{P}{g}=(\vec{x}{1,g},\ldots,\vec{x}{i,g},\ldots,\vec{x}{NP,g}),\ i=1 ,2,...,NP,Pg=(x 1,g,...,x i,g,...,x NP,g), i=1,2,...,NP,

其中 ggg 表示世代索引，g=1,2,...,GMAXg=1,2,\ldots,G_{MAX}g=1,2,...,GMAX。每个向量由DDD个变量组成：

x⃗i,g=(xi,1,g,xi,2,g,...,xi,D,g).\vec{x}{i,g}=(x{i,1,g},x_{i,2,g},...,x_{i,D,g}).x i,g=(xi,1,g,xi,2,g,...,xi,D,g).

包含NPNPNP个向量的随机初始化种群在GMAXG_{MAX}GMAX代中演化，引导搜索空间中的向量朝向全局最优解。在进化过程结束时，即经过GMAXG_{MAX}GMAX代后，DE停止并将适应度最佳的向量作为最终解返回。

在每一代中，DE对每个个体执行三个操作：变异、交叉和选择。

变异：使用一种变异策略创建一个变异向量v⃗i,g\vec{v}_{i,g}v i,g。原始DE算法[2]引入了'DE/rand/1'变异策略，它是DE中最常用的变异策略之一。该策略随机选择两个向量，将它们的差值乘以缩放因子FFF后，加到第三个随机选择的向量上。该策略可以表示为：

v⃗i,g=x⃗r1,g+F⋅(x⃗r2,g−x⃗r3,g),\vec{v}{i,g}=\vec{x}{r_{1},g}+F\cdot(\vec{x}{r{2},g}-\vec{x}{r{3},g}),v i,g=x r1,g+F⋅(x r2,g−x r3,g),

其中r1,r2,r3r_{1}, r_{2}, r_{3}r1,r2,r3是集合{1,NP}\{1, NP\}{1,NP}中的索引。这些索引是随机选择的，需满足两两不同且不同于索引iii：

r1≠r2≠r3≠i.r_{1}\neq r_{2}\neq r_{3}\neq i.r1=r2=r3=i.

其他DE变异策略包括：
- "DE/best/1"：v⃗i,g=x⃗best,g+F(x⃗r1,g−x⃗r2,g)\vec{v}{i,g}=\vec{x}{best,g}+F(\vec{x}{r{1},g}-\vec{x}{r{2},g})v i,g=x best,g+F(x r1,g−x r2,g)
- "DE/current to best/1"：v⃗i,g=x⃗i,g+F(x⃗best,g−x⃗i,g)+F(x⃗r1,g−x⃗r2,g)\vec{v}{i,g}=\vec{x}{i,g}+F(\vec{x}{best,g}-\vec{x}{i,g})+F(\vec{x}{r{1},g}-\vec{x}{r{2},g})v i,g=x i,g+F(x best,g−x i,g)+F(x r1,g−x r2,g)
- "DE/best/2"：v⃗i,g=x⃗best,g+F(x⃗r1,g−x⃗r2,g)+F(x⃗r3,g−x⃗r4,g)\vec{v}{i,g}=\vec{x}{best,g}+F(\vec{x}{r{1},g}-\vec{x}{r{2},g})+F(\vec{x}{r{3},g}-\vec{x}{r{4},g})v i,g=x best,g+F(x r1,g−x r2,g)+F(x r3,g−x r4,g)
- "DE/rand/2"：v⃗i,g=x⃗r1,g+F(x⃗r2,g−x⃗r3,g)+F(x⃗r4,g−x⃗r5,g)\vec{v}{i,g}=\vec{x}{r_{1},g}+F(\vec{x}{r{2},g}-\vec{x}{r{3},g})+F(\vec{x}{r{4},g}-\vec{x}{r{5},g})v i,g=x r1,g+F(x r2,g−x r3,g)+F(x r4,g−x r5,g)
其中索引r1r_{1}r1到r5r_{5}r5表示在范围{1,NP}\{1, NP\}{1,NP}内生成且互不相同的随机整数，并且也不同于索引iii。x⃗best\vec{x}_{best}x best是当前代中的最佳向量。每种策略在维持种群多样性方面有不同的能力，这可能会在进化过程中增加或降低收敛速度。读者可参阅DE的相关综述[3, 4, 5]。
交叉：由一种变异策略生成的变异向量v⃗i,g\vec{v}{i,g}v i,g用于下一个称为交叉的操作。二项式交叉在DE中被广泛使用，另一种交叉是指数交叉[2, 3]。前者按如下方式创建试验向量u⃗i,g\vec{u}{i,g}u i,g：

ui,j,g={vi,j,g,if rand(0,1)≤CR or j=jrand,xi,j,g,ohterwise ,u_{i,j,g}=\begin{cases}v_{i,j,g}, &\text{if }rand(0,1)\leq CR \text{ or } j=j_{rand},\\ x_{i,j,g}, &\text{ohterwise ,}\end{cases}ui,j,g={vi,j,g,xi,j,g,if rand(0,1)≤CR or j=jrand,ohterwise ,

其中i=1,2,...,NPi=1,2,...,NPi=1,2,...,NP且j=1,2,...,Dj=1,2,...,Dj=1,2,...,D。CR∈[0,1]CR\in[0,1]CR∈[0,1]是交叉参数，表示从变异向量为试验向量创建分量的概率。如果某个分量未从变异向量中选择，则从父向量x⃗i,g\vec{x}{i,g}x i,g中获取。随机选择的索引jrand∈{1,2,...,NP}j{rand}\in\{1,2,...,NP\}jrand∈{1,2,...,NP}确保试验向量至少包含变异向量的一个分量。

如果试验向量中的某些变量超出了边界，则会应用重复机制。
选择：交叉操作后，对试验向量进行评估------计算目标函数值f(u⃗i,g)f(\vec{u}{i,g})f(u i,g)。然后，选择操作根据目标函数值比较两个向量：种群向量x⃗i,g\vec{x}{i,g}x i,g及其对应的试验向量u⃗i,g\vec{u}_{i,g}u i,g。较好的向量将成为下一代成员。最小化优化问题的选择操作定义如下：

x⃗i,g+1={u⃗i,g,if f(u⃗i,g)≤f(x⃗i,g),x⃗i,g,otherwise .\vec{x}{i,g+1}=\begin{cases}\vec{u}{i,g}, &\text{if }f(\vec{u}{i,g})\leq f(\vec{x}{i,g}),\\ \vec{x}_{i,g}, &\text{otherwise .}\end{cases}x i,g+1={u i,g,x i,g,if f(u i,g)≤f(x i,g),otherwise .

这种选择操作是贪婪的，是DE所特有的，在其他进化算法中很少应用。

B. L-SHADE 和 iL-SHADE 算法

本节简要介绍L-SHADE[6]和iL-SHADE算法。

L-SHADE[6]算法扩展了基于成功历史自适应的DE（SHADE）[1]算法，加入了线性种群规模缩减机制（LPSR），该机制在每一代后根据线性函数减少种群大小。L-SHADE曾是CEC 2014实数参数单目标优化竞赛中排名最高的基于DE的算法。回顾算法受其前身启发的历史，我们可以看到以下算法之间的密切关系：JADE[16]、SHADE[1]、L-SHADE[6]。之后，又提出了几种其他基于JADE/L/SHADE的算法。

L-SHADE应用current-to-pppBest/1/bin策略生成试验向量，使用加权Lehmer均值（meanwLmeanw_{L}meanwL）使FFF、CRCRCR控制参数自适应。历史记忆有HHH个条目（∣MF∣=∣MCR∣=H|M_{F}|=|M_{CR}|=H∣MF∣=∣MCR∣=H）。在原始DE算法[2]中，所有三个控制参数在进化过程中保持不变，而L-SHADE则自适应地调整缩放因子和交叉参数（FFF和CRCRCR），并在进化过程中缩减种群大小（NPNPNP）。

iL-SHADE[7]算法是L-SHADE算法的扩展版本。

总结一下iL-SHADE[7]算法中提出的主要特性：

CRCRCR控制参数的较高值在优化过程中通过以下方式被传播：
- MCRM_{CR}MCR中的所有历史记忆值初始化为0.8（在L-SHADE中设置为0.5），
- 一个历史记忆条目（在我们的例子中是最后一个，参见算法1中的第10-13行）设置如下：MCR,H=0.9M_{CR,H}=0.9MCR,H=0.9和MF,H=0.9M_{F,H}=0.9MF,H=0.9，并且这些值在进化过程中保持不变。通过这种方式，不仅更高值的CRiCR_{i}CRi更频繁地被使用，其配对的FiF_{i}Fi值也更高。如果CRCRCR值更高，试验向量从变异向量创建分量的概率也更高。
记忆更新机制存储当前代（例如ggg代）的历史记忆值MCRM_{CR}MCR和MFM_{F}MF，并将其与加权Lehmer均值同等加权地用于计算下一代（g+1g+1g+1代）的历史记忆值。
在进化过程的早期阶段，不允许出现非常高的FFF值和非常低的CRCRCR值。
每代ggg之后，下一代（g+1g+1g+1代）中current-to-pppBest/1变异的ppp值计算如下：
p=(pmin−pmaxmax_nfes)⋅nfes+pmax(1)p = \left( \frac{p_{\text{min}} - p_{\text{max}}}{\text{max\nfes}} \right) \cdot \text{nfes} + p{\text{max}} \tag{1}p=(max_nfespmin−pmax)⋅nfes+pmax(1)

其中nfesnfesnfes是当前的目标函数评估次数，max_nfesmax\_nfesmax_nfes是目标函数评估的最大次数。（注：公式（1）与原文中不一致，原文中p为递增的，显然不满足后文中p为线性递减的，可能为作者笔误。）

在iL-SHADE中，与L-SHADE相比，current-to-pppBest/1/bin策略、外部存档、线性种群规模缩减等特性保持不变。

III. JSO -- IL-SHADE的新变体

本节介绍用于解决单目标实数参数优化的一个新变体。我们将其命名为JSO算法。JSO算法的伪代码如算法1所示。它是iL-SHADE算法[7]的扩展版本。在算法1中，我们将在JSO中相对于iL-SHADE算法新增或更改的代码行用⇐符号标记 。

L-SHADE和iL-SHADE应用DE/current-to-pppBest/1变异策略来生成试验向量：

v⃗i,g=x⃗i,g+F(x⃗pBest,g−x⃗i,g)+F(x⃗r1,g−x⃗r2,g),(2)\vec{v}{i,g}=\vec{x}{i,g}+F(\vec{x}{pBest,g}-\vec{x}{i,g})+F(\vec{x}{r{1},g}-\vec{x}{r{2},g}), \tag{2}v i,g=x i,g+F(x pBest,g−x i,g)+F(x r1,g−x r2,g),(2)

而JSO使用一种新的加权版本变异策略，称为DE/current-to-pppBest-w/1，如下所示：

v⃗i,g=x⃗i,g+Fw(x⃗pBest,g−x⃗i,g)+F(x⃗r1,g−x⃗r2,g),(3)\vec{v}{i,g}=\vec{x}{i,g}+F_{w}(\vec{x}{pBest,g}-\vec{x}{i,g})+F(\vec{x}{r{1},g}-\vec{x}{r{2},g}),\tag{3}v i,g=x i,g+Fw(x pBest,g−x i,g)+F(x r1,g−x r2,g),(3)

其中FwF_{w}Fw的计算如下：

Fw={0.7∗F,nfes<0.2max_nfes,0.8∗F,nfes<0.4max_nfes,1.2∗F,otherwise.(4)F_{w}=\begin{cases}0.7*F, &nfes<0.2max\_nfes,\\0.8*F, &nfes<0.4max\_nfes,\\1.2*F, &\text{otherwise}.\end{cases} \tag{4}Fw=⎩ ⎨ ⎧0.7∗F,0.8∗F,1.2∗F,nfes<0.2max_nfes,nfes<0.4max_nfes,otherwise.(4)

所提出的加权变异策略的目的是：在进化过程的早期阶段，对包含x⃗pBest,g\vec{x}{pBest,g}x pBest,g的向量差应用较小的因子FwF{w}Fw进行缩放；而在后期阶段则使用较大的因子FwF_{w}Fw。通过因子FwF_{w}Fw，向量x⃗pBest,g\vec{x}_{pBest,g}x pBest,g可能产生较低和/或较高的影响力。公式（4）中的数值以及算法1中第19-27行的数值是基于一些额外实验设置的，但未对这些数值（参数）进行精细调整。

可以注意到，从iL-SHADE到JSO的更改和扩展是微小的------iL-SHADE的主要特性保持不变。而且，iL-SHADE和L-SHADE之间的差异也并不大[7]。因此，在下一节中，我们将主要侧重于比较JSO与L-SHADE的性能，同时也会给出所有三种算法的总结性结果。

IV. 实验（EXPERIMENTS）

A. 评估方法（Evaluation Method）

CEC 2017的评估方法结合了由公式（6）和（7）定义的两个分数来计算最终得分，如下所示：
score=score1+score2(5)\text{score} = \text{score}_1 + \text{score}_2 \tag{5}score=score1+score2(5)

其中
score1=(1−SE−SEmin⁡SE)×50(6)\text{score}1 = \left(1 - \frac{SE - SE{\min}}{SE}\right) \times 50 \tag{6}score1=(1−SESE−SEmin)×50(6)

这里，SEminSE_{min}SEmin 是所有算法中误差总和的最小值，SESESE 是所有维度的误差值总和，其定义如下：
SE=0.1×∑i=130ef10D+0.2×∑i=130ef30D+0.3×∑i=130ef50D+0.4×∑i=130ef100DSE = 0.1 \times \sum_{i=1}^{30} ef_{10D} + 0.2 \times \sum_{i=1}^{30} ef_{30D} + 0.3 \times \sum_{i=1}^{30} ef_{50D} + 0.4 \times \sum_{i=1}^{30} ef_{100D} SE=0.1×i=1∑30ef10D+0.2×i=1∑30ef30D+0.3×i=1∑30ef50D+0.4×i=1∑30ef100D

其中 efefef 是所有函数的误差值。

然后
score2=(1−SR−SRmin⁡SR)×50(7)\text{score}2 = \left(1 - \frac{SR - SR{\min}}{SR}\right) \times 50 \tag{7}score2=(1−SRSR−SRmin)×50(7)

其中 SRminSR_{min}SRmin 是所有算法中排名总和的最小值，SRSRSR 是排名总和，定义如下：
SR=0.1×∑i=130rank10D+0.2×∑i=130rank30D+0.3×∑i=130rank50D+0.4×∑i=130rank100DSR = 0.1 \times \sum_{i=1}^{30} \text{rank}{10D} + 0.2 \times \sum{i=1}^{30} \text{rank}{30D} + 0.3 \times \sum{i=1}^{30} \text{rank}{50D} + 0.4 \times \sum{i=1}^{30} \text{rank}_{100D}SR=0.1×i=1∑30rank10D+0.2×i=1∑30rank30D+0.3×i=1∑30rank50D+0.4×i=1∑30rank100D

在该评估方法中，更高的维度被赋予了更高的权重。

B. 实验结果（Experimental Results）

我们在为CEC 2017特别会议[23]提供的可扩展基准函数上测试了jSO算法。本次特别会议中基准函数的维度为 D=10,30,50D=10, 30, 50D=10,30,50 和 100100100。所有基准函数的最优解值是预先已知的。算法需要对每个函数执行51次独立运行，目标函数的最大评估次数 max_nfesmax\_nfesmax_nfes 为 D×10,000D \times 10,000D×10,000。存在CEC 2017基准函数的源代码，但算法需要将这些函数作为黑盒使用，即没有关于基准函数结构的明确知识。

PC配置：

系统：GNU Linux，CPU：Intel® Core™ i7-4770 CPU 3.4 GHz，内存：16 GB，编程语言：C++，算法：jSO，编译器：g++ (GNU编译器)。

jSO中的参数根据L-SHADE和iL-SHADE算法中的参数设置保持不变，除了以下参数：

变异策略使用 current-to-pppBest-w/1（L-SHADE和iL-SHADE中使用的是current-to-pppBest/1），
变异策略中的 ppp 值在进化过程中从 pmaxp_{max}pmax 线性减小到 pminp_{min}pmin ，其中jSO中 pmax=0.25p_{max}=0.25pmax=0.25（iL-SHADE中为0.2），pmin=pmax/2p_{min}=p_{max}/2pmin=pmax/2（在L-SHADE中 ppp 固定为0.11），
初始种群大小 Ninit=25log⁡(D)DN^{init}=25\log(D)\sqrt{D}Ninit=25log(D)D （L-SHADE中设为18D18D18D，而iL-SHADE中设为12D12D12D），
历史记忆大小 H=5H=5H=5（L-SHADE和iL-SHADE中为H=6H=6H=6），
MFM_{F}MF 值初始化为0.3（L-SHADE和iL-SHADE中为0.5）。

所得结果呈现在表I、II、III和IV中。在这些表中，按照[23]的要求，给出了误差值 f(x⃗)−f(x⃗∗)f(\vec{x})-f(\vec{x}^{*})f(x )−f(x ∗)。计算了51次运行中每次找到的最佳适应度值与真实最优值之间的误差值，然后在表格的每一列中给出了这些误差值的最佳值、最差值、中位数、平均值和标准差。

表I 在10维时jSO算法的结果。

表II 在30维时jSO算法的结果。

表III 在50维时jSO算法的结果。

表IV 在100维时jSO算法的结果。

接下来，我们比较了jSO和L-SHADE算法的性能。结果分别在表V、VI、VII和VIII中针对每个维度给出。这些表中显示了jSO和L-SHADE算法的平均值和标准差，并在一个单独的列中显示了统计检验结果。符号 +,−,≈+, -, \approx+,−,≈ 表示基于显著性水平为0.05的威尔科克森秩和检验，与L-SHADE算法相比，提出的jSO算法表现显著更好（+++）、显著更差（−-−）或性能差异无统计学意义（≈\approx≈）。

表 V jSO 与 L-SHADE 在维度 D = 10 下所得结果的比较。威尔科克森秩和检验（α = 0.05）。

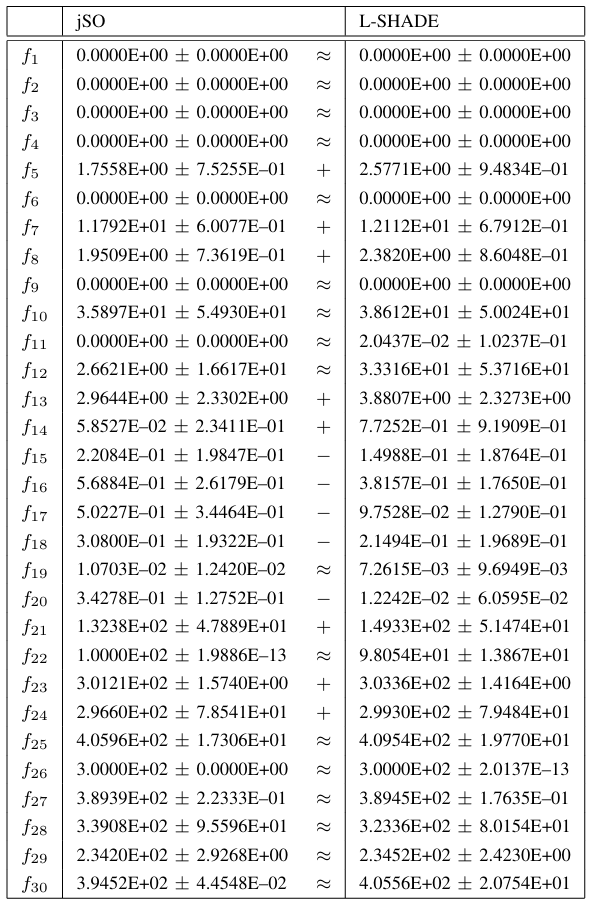
表 VI jSO 与 L-SHADE 在维度 D = 30 下所得结果的比较。威尔科克森秩和检验（α = 0.05）。

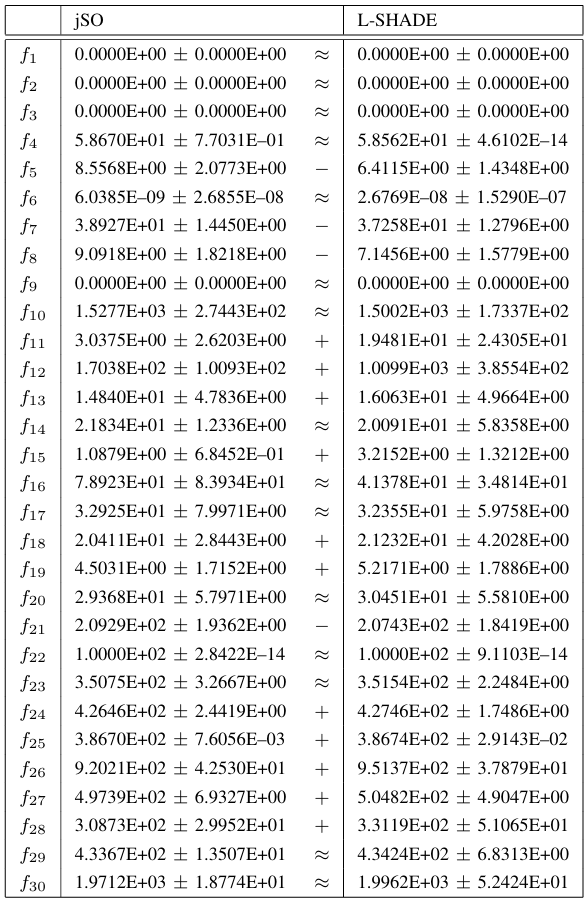
表 VII jSO 与 L-SHADE 在维度 D = 50 下所得结果的比较。威尔科克森秩和检验（α = 0.05）。

表 VIII jSO 与 L-SHADE 在维度 D = 100 下所得结果的比较。威尔科克森秩和检验（α = 0.05）。

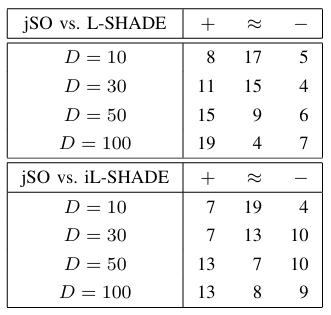
统计检验的总结结果呈现在表IX中。如果我们比较胜（+++）和负（−-−）的数量，可以看到在除一个例外（在 D=30D=30D=30 时iL-SHADE表现优于jSO）的所有维度上，jSO均表现出比L-SHADE和iL-SHADE更好的性能。jSO的优越性能在 D=100D=100D=100 时尤为明显。

表 IX 总结性统计检验结果表明，与 L-SHADE 及 iL-SHADE 相比，jSO 算法表现显著更好 (+)、显著更差 (-)，或性能差异无统计学意义显著性差异 (≈)（基于威尔科克森秩和检验，显著性水平为 0.05）。

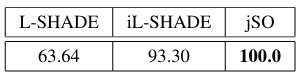
表X展示了根据第四部分A节所述评估方法得到的得分。在此方法中，得分越高越好。可以看出，jSO获得了最高分，其次是iL-SHADE和L-SHADE。

表 X L-SHADE、iL-SHADE 和 jSO 的评估方法得分。

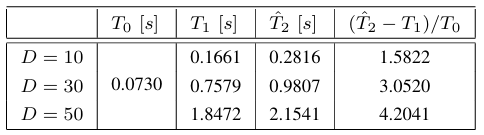
表XI展示了jSO算法的复杂度。需要注意的是，由于测得的运行时间值非常小，该复杂度应审慎考量。

表 XI JSO算法的运行时间复杂度

V. 结论（CONCLUSIONS）

本文提出了一种名为 jSO 的新型差分进化算法，用于解决单目标实数参数优化问题。该算法基于 iL-SHADE 算法，并引入了一种新的加权变异策略 DE/current-to-pBest-w/1。

通过使用 CEC 2017 特别会议的基准函数进行评估，jSO 在不同维度（D=10,30,50,100D = 10, 30, 50, 100D=10,30,50,100）上均表现出卓越的性能。统计显著性检验（Wilcoxon 秩和检验，α=0.05\alpha = 0.05α=0.05）结果表明，在大多数测试函数和维度上，jSO 的性能显著优于其前身 L-SHADE。与 iL-SHADE 相比，jSO 也显示出具有竞争力或更好的结果，尤其是在较高维度（如 D=100D = 100D=100）问题上优势更为明显。

根据 CEC 2017 的评估方法，jSO 在最终得分上超过了 L-SHADE 和 iL-SHADE，取得了三者中的最佳成绩。运行时间分析表明，算法复杂度随问题维度增加而增长，但所有测量到的绝对运行时间都相对较小。

总之，jSO 通过引入简单而有效的加权变异策略，在保持算法框架基本不变的情况下，显著提升了原 iL-SHADE 和 L-SHADE 算法的优化性能，特别是在高维问题上。未来的工作可能包括进一步优化参数设置、探索策略组合，以及将 jSO 应用于更广泛的现实世界优化问题。

参考文献（Reference）

$1\] R. Tanabe and A. Fukunaga, "Evaluating the performance of SHADE on CEC 2013 benchmark problems," in 2013 IEEE Congress on Evolutionary Computation (CEC), June 2013, pp. 1952--1959.$
$3\] S. Das and P. Suganthan, "Differential evolution: A survey of the stateof-the-art," IEEE Transactions on Evolutionary Computation, vol. 15, no. 1, pp. 27--54, 2011.$
$5\] S. Das, S. S. Mullick, and P. N. Suganthan, "Recent advances in differential evolution--an updated survey," Swarm and Evolutionary Computation, vol. 27, pp. 1--30, 2016.$
$7\] J. Brest, M. S. Mauˇcec, and B. Boˇskovic ́, "iL-SHADE: Improved LSHADE algorithm for single objective real-parameter optimization," in IEEE Congress on Evolutionary Computation (CEC) 2016. IEEE, 2016, pp. 1188--1195.$
$9\] B. Boˇskovic ́ and J. Brest, "Differential evolution for protein folding optimization based on a three-dimensional AB off-lattice model," Journal of Molecular Modeling, vol. 22, pp. 1--15, 2016.$
$11\] R. P. Parouha and K. N. Das, "A memory based differential evolution algorithm for unconstrained optimization," Applied Soft Computing, vol. 38, pp. 501--517, 2016.$
$13\] I. Poikolainen, F. Neri, and F. Caraffini, "Cluster-based population initialization for differential evolution frameworks," Information Sciences, vol. 297, pp. 216--235, 2015.$
$15\] J. Brest, S. Greiner, B. Boˇskovi ́c, M. Mernik, and V. Zˇ umer, "SelfAdapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems," IEEE Transactions on Evolutionary Computation, vol. 10, no. 6, pp. 646--657, 2006.$
$17\] J. Brest and M. S. Mauˇcec, "Population Size Reduction for the Differential Evolution Algorithm," Applied Intelligence, vol. 29, no. 3, pp. 228--247, 2008.$
$19\] N. Awad, M. Ali, and R. Reynolds, "A differential evolution algorithm with success-based parameter adaptation for CEC2015 learning-based optimization," in 2015 IEEE Congress on Evolutionary Computation (CEC), May 2015, pp. 1098--1105.$
$21\] N. H. Awad, M. Z. Ali, P. N. Suganthan, and R. G. Reynolds, "An ensemble sinusoidal parameter adaptation incorporated with L-SHADE for solving CEC2014 benchmark problems," in IEEE Congress on Evolutionary Computation (CEC) 2016. IEEE, 2016, pp. 2958--2965.$
$23\] N. H. Awad, M. Z. Ali, B. Y. Q. J. J. Liang, and P. N. Suganthan, "Problem Definitions and Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Bound Constrained Real-Parameter Numerical Optimization," Nanyang Technological University, Singapore, Tech. Rep., November 2016. \[Online\]. Available: http://www.ntu.edu.sg/home/epnsugan/$