二叉树题目
1、选择题
1.1、二叉树的一点性质
二叉树有这样一条性质:
度为 0 的节点个数 = 度为 2 的节点个数 + 1 度为0的节点个数=度为2的节点个数+1 度为0的节点个数=度为2的节点个数+1这是怎么得到的?
我们在前面对于树的简单介绍中提到,树的节点个数与边数有这样一种关系:
树的边数 = 树的节点个数 − 1 树的边数=树的节点个数-1 树的边数=树的节点个数−1这很好理解,因为两个节点中间连接一条边。
我们假设,度为0节点的个数为n0,度为1节点的个数为n1,度为2节点的个数为n2。
那么边数可以表示为:
边数 = n 0 + n 1 + n 2 − 1 边数=n_0+n_1+n_2-1 边数=n0+n1+n2−1我们再来看一棵二叉树:
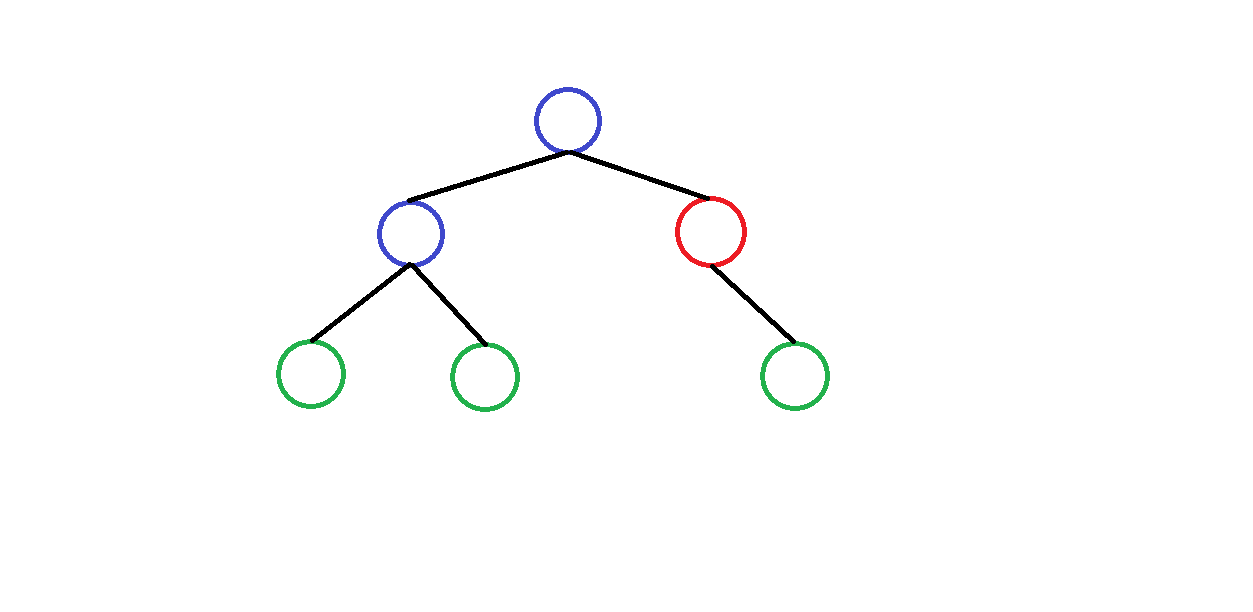
不难看出,度为0的节点,其下面有0条边;度为1的节点,其下面有1条边;度为2的节点,其下面有2条边。
所以边数又可以表示为:
边数 = 2 ∗ n 2 + n 1 边数=2*n_2+n_1 边数=2∗n2+n1联立上面边数与n0、n1、n2的关系式,得到:
n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1得证。
1.2、一些例题
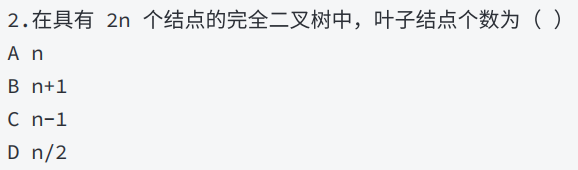
这道题中,我们假设度分别为0、1、2的节点个数分别为:
n 0 、 n 1 、 n 2 n_0、n_1、n_2 n0、n1、n2那么 2 n = n 0 + n 1 + n 2 . . . . . . ① 2n=n_0+n_1+n_2......① 2n=n0+n1+n2......①我们在前面知道 n0 与 n2 的关系:
n 0 = n 2 + 1...... ② n_0=n_2+1......② n0=n2+1......②联立①②,得:
2 n = 2 n 0 + n 1 − 1 2n=2n_0+n_1-1 2n=2n0+n1−1那么关键来了, n1 是多少?
我们知道,在一个有k 层的完全二叉树中,第k层都是叶子节点,前k-2层中所有节点度为2。
对于k-1 层中的节点,如果第k 层的节点个数为偶数,假设有 2x 个,意味着在第k-1层中,有 x 个节点度为2,剩下 (2^(k-2)-x)个节点度为0。也就是说,当第k层的节点个数为偶数,即整个完全二叉树节点个数为奇数时,整个完全二叉树没有度为1的节点。
然而,对于k-1 层中的节点,如果第k 层的节点个数为奇数,意味着在第k-1层中,有且只有一个节点,它的度为1。也就是说,当第k层的节点个数为奇数,即整个完全二叉树节点个数为偶数时,整个完全二叉树有且只有1个度为1的节点。
在这道题中,完全二叉树结点的个数为偶数,所以 n1 == 1 。那么n0==n,即叶子节点有n个。
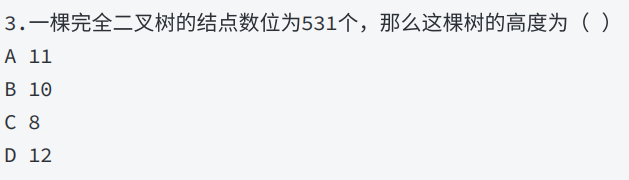
题中提到了完全二叉树,而我们知道满二叉树中,总结点个数n与树的深度h存在关系:
n = 2 k − 1 n=2^k-1 n=2k−1
所以,一个完全二叉树节点的个数,应该是介于,深度比其小一层的满二叉树(节点个数),和深度相同的满二叉树(节点个数),之间的。
那么可以做一个表:
| 深度 | 对应满二叉树的节点个数 |
|---|---|
| 8 | 255 |
| 9 | 511 |
| 10 | 1023 |
不难得出,这棵树的高度是10。
设⼀课二叉树的中序遍历序列: b a d c e ,后序遍历序列: b d e c a ,求二叉树前序遍历序列 设⼀课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,求二叉树前序遍历序列 设⼀课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,求二叉树前序遍历序列
在这道题中,我们根据后序遍历序列可以知道,二叉树的根节点为a。
那么,我们回到中序遍历序列,以a为界,b是a的左子树(部分),dce是a的右子树(部分)。
对于c、d、e,中序遍历序列为dce(左根右),后序遍历序列为dec(左右根),所以,d、e分别为c的左、右孩子。
那么树为:
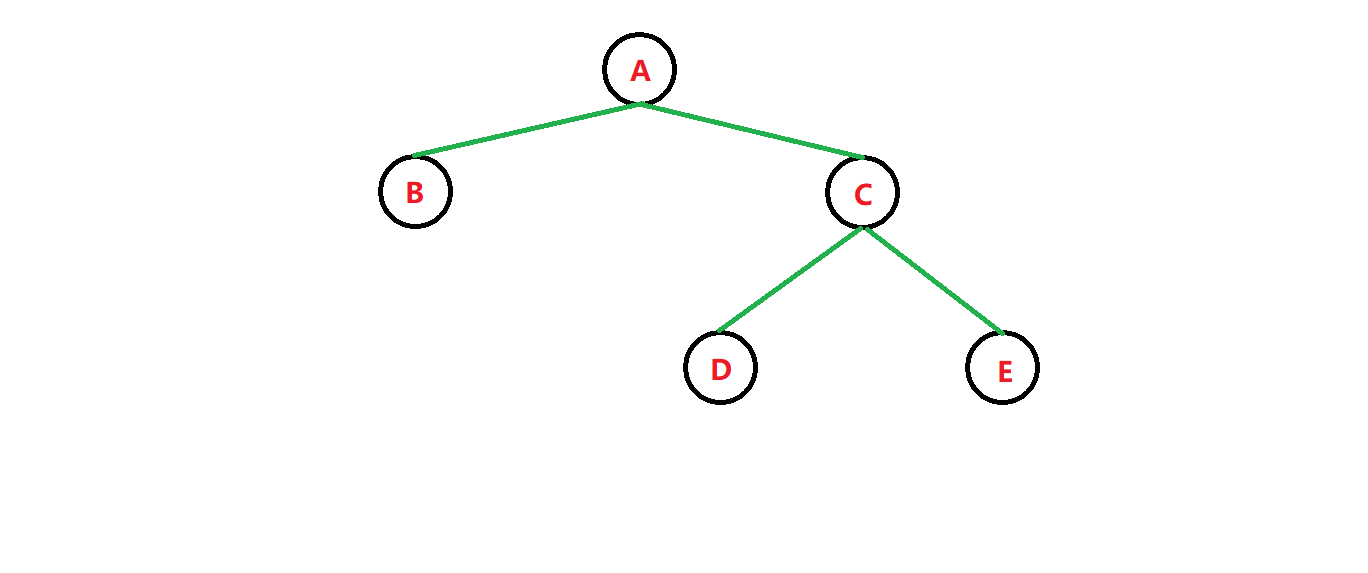
前序遍历序列: a − > b − > c − > d − > e a->b->c->d->e a−>b−>c−>d−>e

我们看到后序遍历序列,F在末尾,所以F为根节点。
那么在中序遍历序列中,F只有左子树ABCDE,没有右子树。
同理,在后序序列ABCDE 中,E在末尾,E只有左子树ABCD。
在后序序列ABCD 中,D在末尾,D只有左子树ABC。
...
那么,树为:
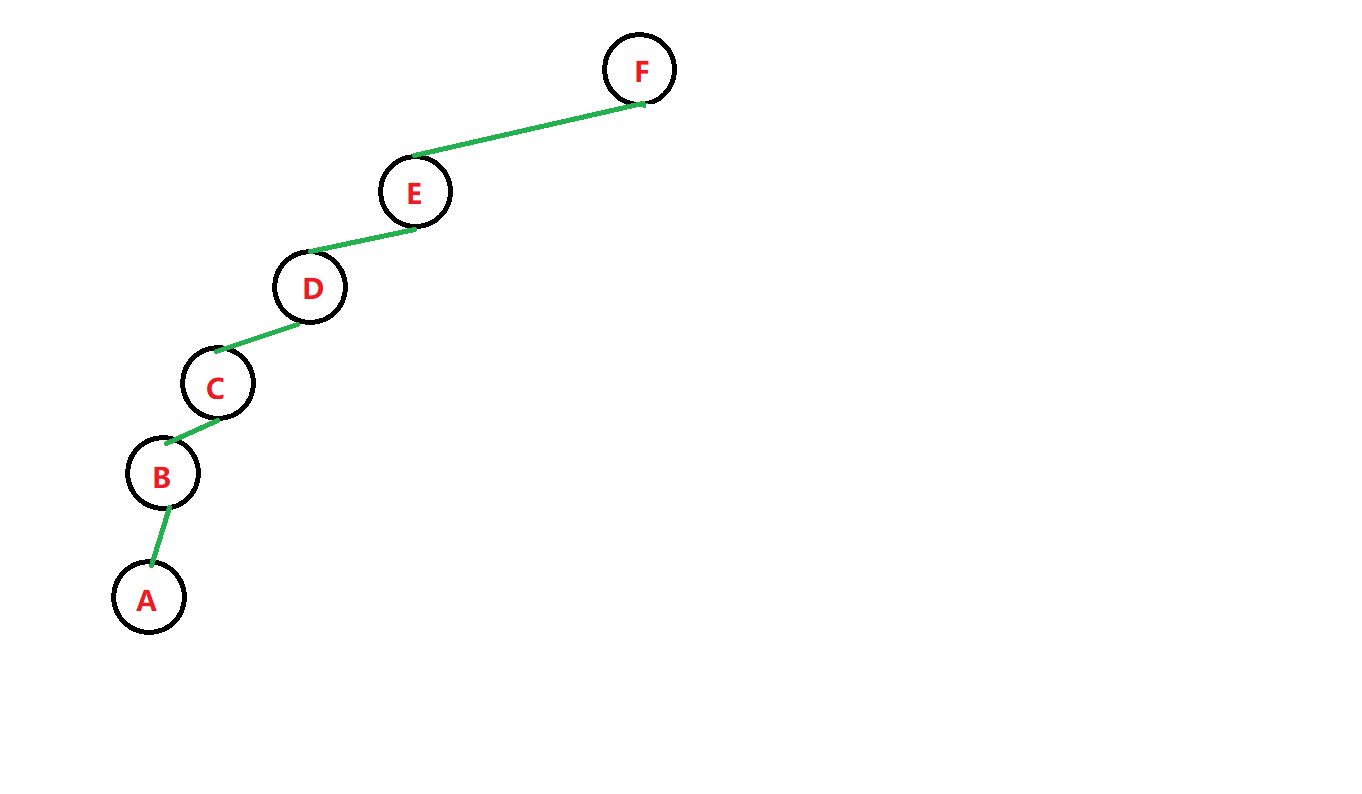
层序序列: F − > E − > D − > C − > B − > A F->E->D->C->B->A F−>E−>D−>C−>B−>A
2、编程题
2.1、单值二叉树

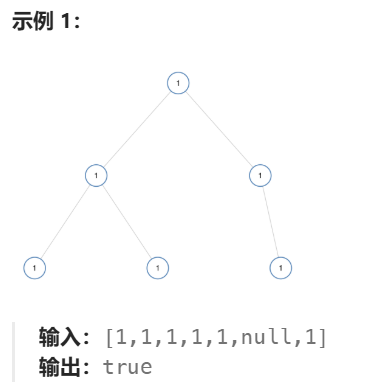
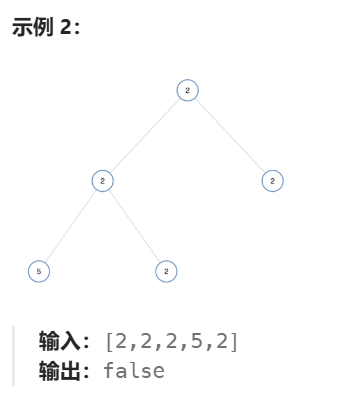
思路是利用递归:
- 判断当前节点是否为空,如果为空,返回
true - 判断当前节点的左孩子是否存在 ,以及值是否与父节点的不相等
- 判断当前节点的右孩子是否存在 ,以及值是否与父节点的不相等
- 若能走到这一步,递归到左、右子树
c
//等号的传递性
//为空,返回真
//根节点与左右子树比较
//如果左右子树存在且与根节点不同,就不是
//继续找左右子树的
bool isUnivalTree(struct TreeNode* root) {
//判空
if (root == NULL)
{
return true;
}
//左孩子
if (root->left && root->left->val != root->val)
{
return false;
}
//右孩子
if (root->right && root->right->val != root->val)
{
return false;
}
// 到左子树 到右子树
return isUnivalTree(root->left) && isUnivalTree(root->right);
}可以将每一个节点看做一个函数栈帧,然后画图走一遍看看。
2.2、相同的树
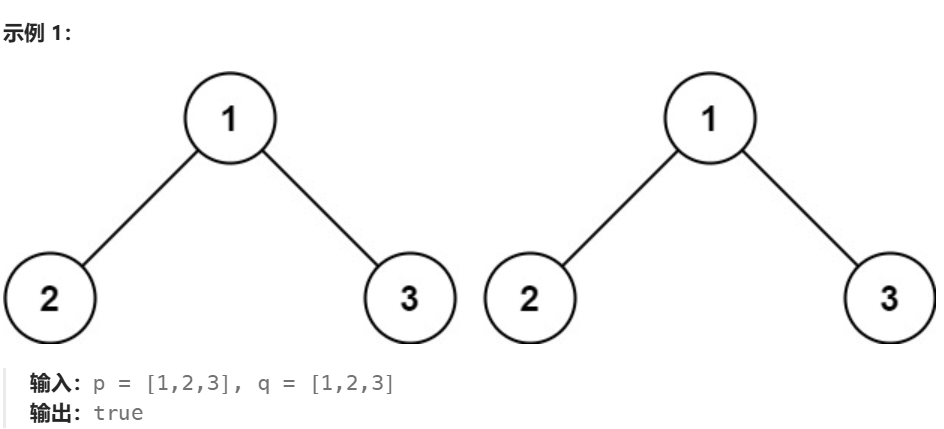
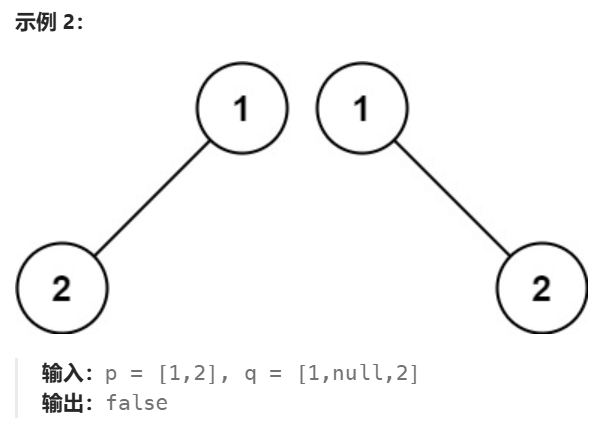
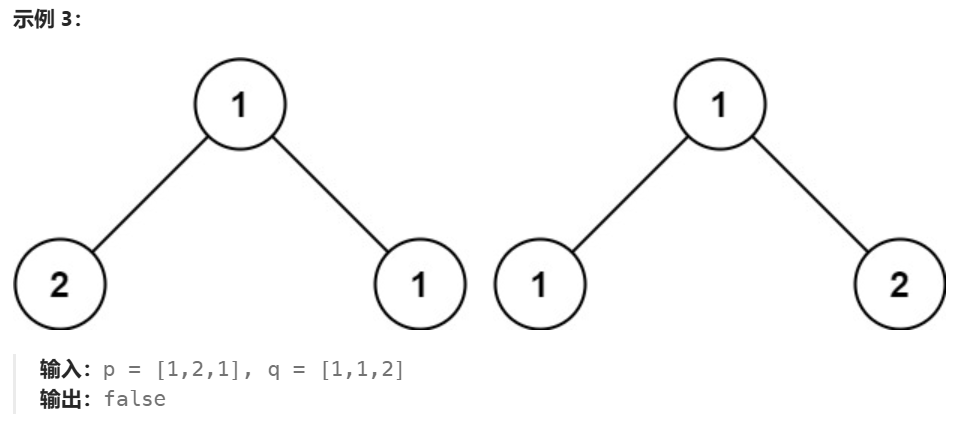
在示例中,我们可以看出,两个二叉树是否相同,除了看节点存储的值 是否相同,还要看树的结构是否相同,即会不会出现一个树当前位置有节点,而另一个树当前位置无节点的情况。
所以思路:
- 判断当前两个节点是否为空,若为空,说明一致,返回真
- 判断当前两个节点是否一个空,一个非空,若是,返回假
- 走到这一步,说明结构相同,则比较存储的值
- 走到这,当前位置相同,递归到左、右子树
c
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
//都为空,返回真
if (p == NULL && q == NULL)
{
return true;
}
//一个空,另一个非空,说明结构不同,返回假
if (p == NULL || q == NULL)
{
return false;
}
//都不为空,比较值
if (p->val != q->val)
{
return false;
}
//走到这,说明目前相同,递归
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
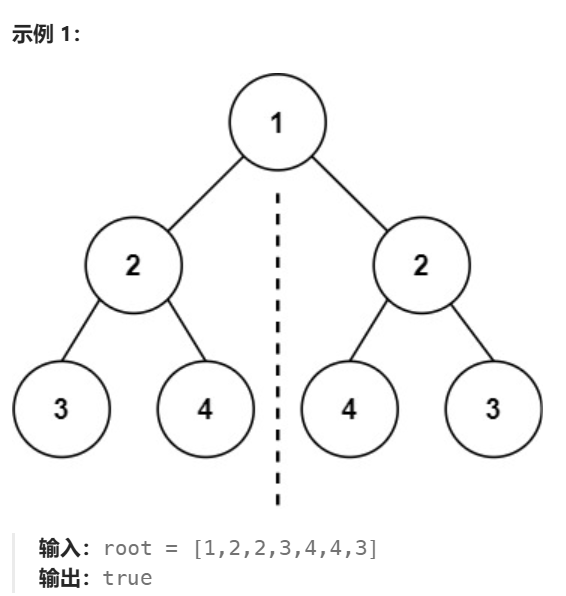
}2.3、对称二叉树
这里我们对上面这棵对称二叉树进行分析。
我们不难知道,分析的其实是二叉树根节点的左、右子树是否对称。此时我们很容易想到利用上面相同的树 代码实现,只不过需要注意,当左子树节点递归到其左孩子时,右子树节点就要递归到其右孩子。
c
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
//判断当前节点是否都为空
if (p == NULL && q == NULL)
{
return true;
}
//判断当前节点是否一个为空,一个不为空,即结构是否相同
if (p == NULL || q == NULL)
{
return false;
}
//走到这,说明节点存在且结构相等,则判断值
if (p->val != q->val)
{
return false;
}
//走到这,说明当前节点没问题,则进入左子树、右子树
return isSameTree(p->left, q->right) && isSameTree(p->right, q->left);
}
bool isSymmetric(struct TreeNode* root) {
if (root == NULL)
{
return true;
}
return isSameTree(root->left, root->right);
}2.4、另一棵树的子树
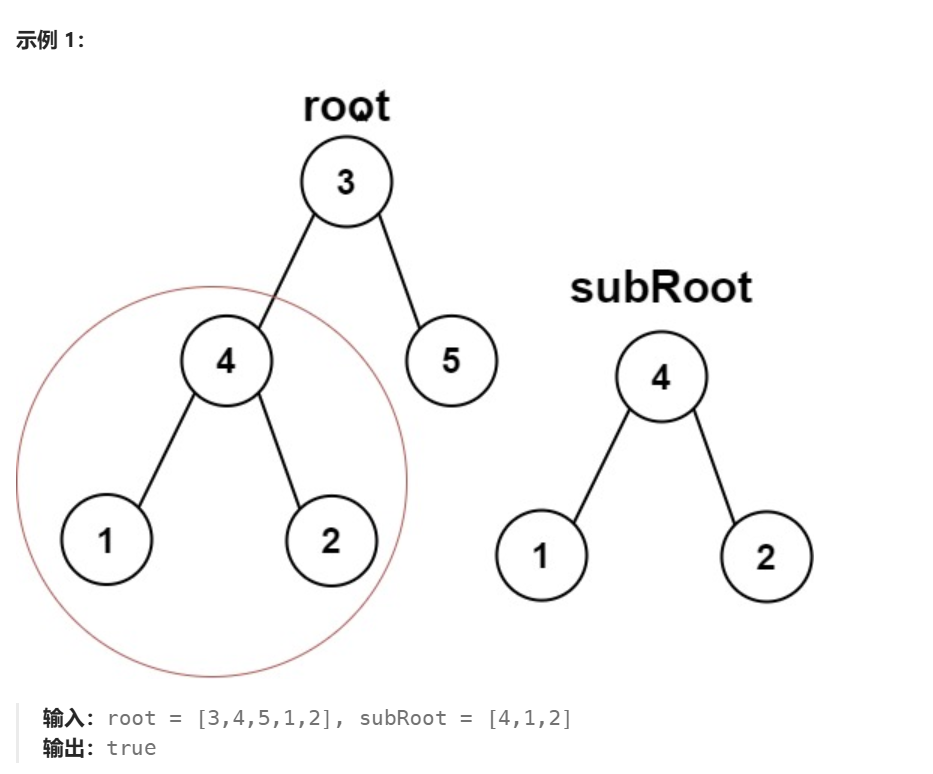
根据题目看两个示例。第一个示例中,根节点的左子树恰好与另一个树相同,所以返回true。
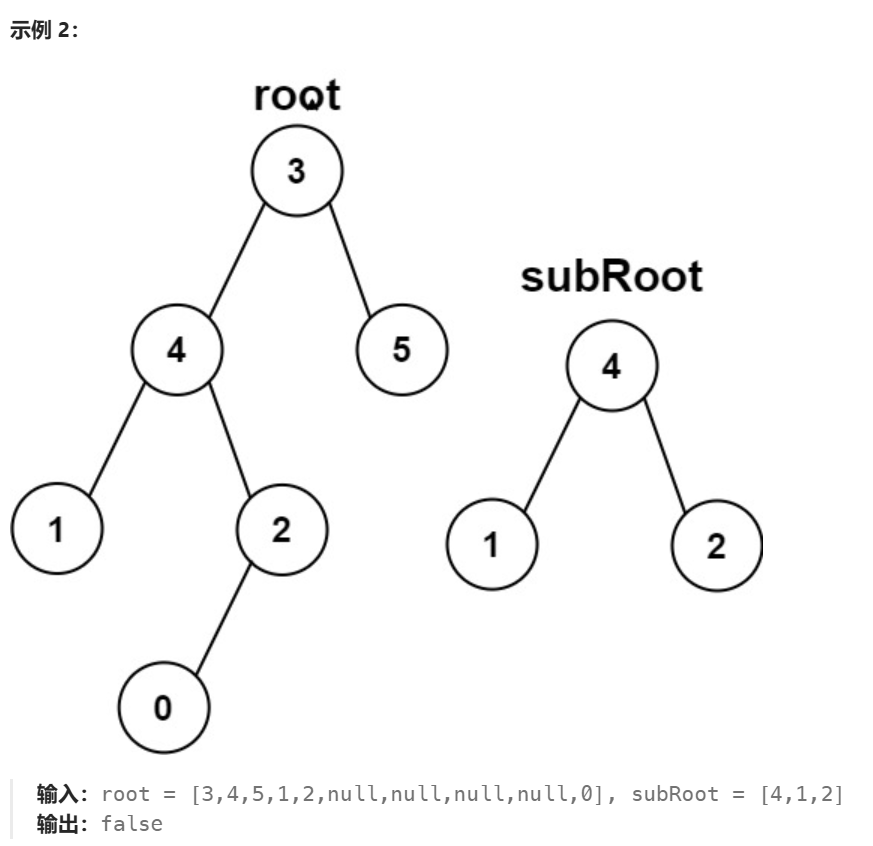
但在第二个示例,尽管根节点的左子树与另一个子树非常相似,但是根节点左子树2节点上多了一个0节点,这是不同的,所以返回false。
根据以上分析,我们可以推理得知,需要另外构建一个判断两树是否相等的函数,这在之前已经实现过了。
继续分析,当,当前节点为空,也就不存在子树了,返回false。
当,当前节点满足要求(两树是否相等函数返回true ),则返回true。
走到这一步,则继续比较左、右子树与另一个树。
c
typedef struct TreeNode TreeNode;
bool isSametree(TreeNode* p, TreeNode* q)
{
//判断是否都为空
if (p == NULL && q == NULL)
{
return true;
}
//判断结构是否相同
if (p == NULL || q == NULL)
{
return false;
}
//判断值是否相同
if (p->val != q->val)
{
return false;
}
//递归到左右子树
return isSametree(p->left, q->left) && isSametree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
//先去构建检查相同树的代码
//当主树为空,也就没有什么子树了
if (root == NULL)
{
return false;
}
//当当前节点之下的树与另一树相同,返回真
if (isSametree(root, subRoot))
{
return true;
}
//到这里,说明当前节点以下的树不满足要求,找左右子树
//只要有一个递归函数返回true,就满足条件
return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
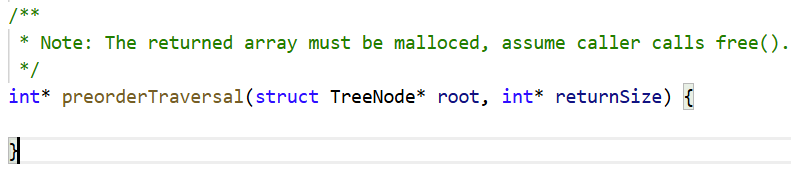
}2.5、二叉树的前、中、后序遍历
这里的前、中、后序遍历,可能与之前我们在实现数据结构的遍历不太一样。
以前序遍历为例。
我们看到第三幅图,图中除了注释要求我们动态开辟 数组空间存储节点数据,还在函数中添加了参数int* returnSize,说明对于二叉树结点个数,我们事先是不知道的。
要开辟空间,就要知道节点个数;而要知道节点个数,我们可以利用之前学过的二叉树求节点个数的知识,构建函数。
开辟完空间。由于前序遍历涉及递归,所以我们不妨另外构建一个真正实现前序遍历的函数。
在这个函数中,由于需要向数组中存储数据,所以我们可以添加数组参数 。而每存完一个节点数据,数组下标都要向前进一位 。这时我们又知道,不能定义局部变量或全局变量,那么就再添加一个(指针)参数,做数组下标。
c
typedef struct TreeNode TreeNode;
int BinaryTreeSize(TreeNode* root)
{
//节点为空,返回0
if (root == NULL)
{
return 0;
}
return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}
void preOrder(TreeNode* root, int* arr, int* pi)
{
//为空,直接返回
if (root == NULL)
{
return;
}
//入数据时,下标不能使用局部变量,也不能使用全局变量
//所以,另外添加一个参数
arr[(*pi)++] = root->val;//修改顺序
preOrder(root->left, arr, pi);
preOrder(root->right, arr, pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
//首先,节点的个数未知,先构建函数求节点个数
*returnSize = BinaryTreeSize(root);
//动态申请数组
int* arr = (int*)malloc(sizeof(int) * (*returnSize));
//构建函数入数组
int i = 0;
preOrder(root, arr, &i);
return arr;
}中、后序遍历,就不再赘述,只要在函数preOrder()改变遍历与存值的顺序即可。
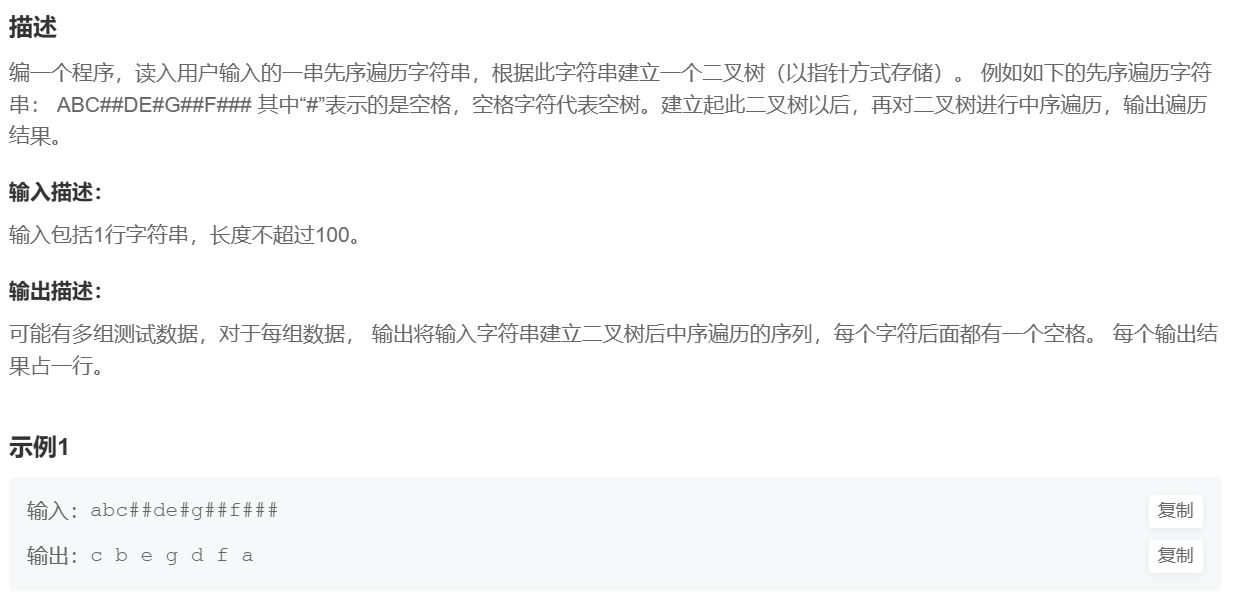
2.6、二叉树遍历
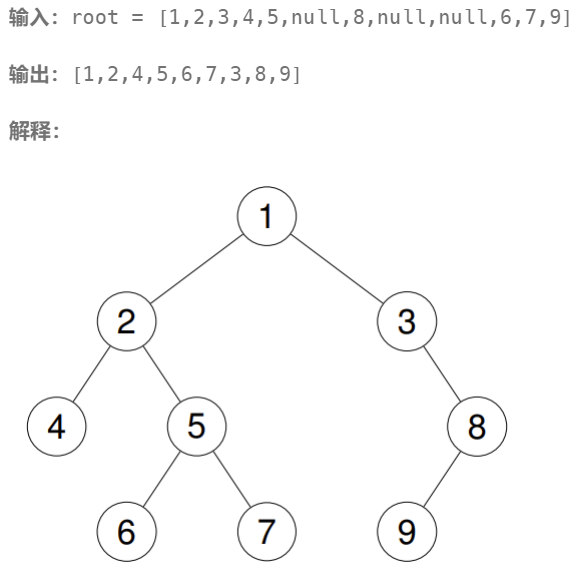
在这里,我们需要根据一个二叉树的前序遍历序列,构建二叉树,再输出这个二叉树的中序遍历序列。
首先,我们设计代码,输入一串字符,代表二叉树的前序序列。
首先设计还原二叉树 的函数,那么函数的返回值为二叉树节点类型 。前序序列中,当读取到 # ,说明在二叉树中读取到了NULL,返回 NULL ,但要数组下标前进一个元素空间大小;
当读到字符,创建节点,数组下标前进,再进入到左、右子树。
其次是中序遍历函数了,前面已经学习过了,这里也不再赘述。
当然,我们还是要在这道题中,另外实现二叉树的定义 、节点的创建这两种功能。
c
#include<stdio.h>
#include<stdlib.h>
#include<errno.h>
//创建二叉树结构
typedef struct TreeNode
{
char val;
struct TreeNode* left;
struct TreeNode* right;
}TreeNode;
//创建节点
TreeNode* BuyNode(char val)
{
TreeNode* newnode = (TreeNode*)malloc(sizeof(TreeNode));
if (newnode == NULL)
{
perror("malloc failed\n");
exit(1);
}
newnode->val = val;
newnode->left = newnode->right = NULL;
return newnode;
}
//根据前序遍历,构建二叉树
TreeNode* createTree(char* str, int* pi)
{
//遇到 # ,说明遇到NULL,返回NULL
if (str[(*pi)] == '#')
{
(*pi)++;//跳过当前 #
return NULL;
}
//创建根节点
TreeNode* root = BuyNode(str[(*pi)++]);
//创建左子树
root->left = createTree(str, pi);
//创建右子树
root->right = createTree(str, pi);
return root;
}
//中序遍历
void InOrder(TreeNode* root)
{
if (root == NULL)
{
return;
}
InOrder(root->left);
printf("%c ", root->val);
InOrder(root->right);
}
int main()
{
char str[100];
scanf("%s", str);
//创建二叉树结构
//根据前序遍历,构建二叉树
int i = 0;
TreeNode* root = createTree(str, &i);
//输出中序遍历
InOrder(root);
return 0;
}