1.6
- 假设一个经济体系有农业、矿业和制造业三个部门.农业部门销售它的产出的5%给矿业部门,30%给制造业部门,保留余下的产出.矿业部门销售它的产出的20%给农业部门,70%给制造业部门,保留余下的产出.制造业部门销售它的产出的20%给农业部门,30%给矿业部门,保留余下的产出.构建该经济体系的交易表,表中的列给出各个部门的产出如何分配给其他部门
解答 :
将比例用小数表示,由于要考虑所有的产出,故每列的元素之和等于1,每一列代表该部门的产出。
交易表
| 采购部门 | 农业 | 矿业 | 制造业 |
|---|---|---|---|
| 农业 | 0.65 | 0.20 | 0.20 |
| 矿业 | 0.05 | 0.10 | 0.30 |
| 制造业 | 0.30 | 0.70 | 0.50 |
结论 :
交易表如上所示,每列表示该部门产出的分配比例,列和为1。
- 假设一个经济体系只有商品和服务两个部门.在每一年中,商品部门销售它的总产出的80%给服务部门,而保留余下的产出;服务部门销售它的总产出的70%给商品部门,保留余下的产出.找出商品和服务部门的年度产出的平衡价格,使得每一部门的收支平衡.
解答 :
逐年填写交易表,每列小数之和为1。
交易表
| 采购部门 | 商品 | 服务 |
|---|---|---|
| 商品 | 0.2 | 0.7 |
| 服务 | 0.8 | 0.3 |
设 pGp_GpG 和 pSp_SpS 分别为商品和服务部门的总产出(美元)。
商品部门平衡方程:pG=0.2pG+0.7pSp_G = 0.2p_G + 0.7p_SpG=0.2pG+0.7pS
服务部门平衡方程:pS=0.8pG+0.3pSp_S = 0.8p_G + 0.3p_SpS=0.8pG+0.3pS
移项整理得:
{0.8pG−0.7pS=0−0.8pG+0.7pS=0 \begin{cases} 0.8p_G - 0.7p_S = 0 \\ -0.8p_G + 0.7p_S = 0 \end{cases} {0.8pG−0.7pS=0−0.8pG+0.7pS=0
增广矩阵行化简:
0.8−0.70−0.80.70\]∼\[1−0.8750000\] \\begin{bmatrix} 0.8 \& -0.7 \& 0 \\\\ -0.8 \& 0.7 \& 0 \\end{bmatrix} \\sim \\begin{bmatrix} 1 \& -0.875 \& 0 \\\\ 0 \& 0 \& 0 \\end{bmatrix} \[0.8−0.8−0.70.700\]∼\[10−0.875000
通解为 pG=0.875pSp_G = 0.875p_SpG=0.875pS,pSp_SpS 自由。
结论 :
一组平衡价格为 pS=1000, pG=875p_S = 1000,\ p_G = 875pS=1000, pG=875。若用分数表示,pG=78pSp_G = \frac{7}{8}p_SpG=87pS,可取 pS=80, pG=70p_S = 80,\ p_G = 70pS=80, pG=70。只有价格比例重要,经济均衡不受价格按比例缩放的影响。
考虑一个由燃料动力、化学金属和机器三个部门构成的经济体系.化学金属部门销售30%的产出给燃料动力部门和50%的产出给机器部门,保留余下的产出.燃料动力部门销售80%的产出给化学金属部门和10%的产出给机器部门,保留余下的产出.机器部门销售40%的产出给化学金属部门和40%的产出给燃料动力部门,保留余下的产出.
a. 构建该经济体系的交易表.
b. 建立方程组表示各部门收支平衡的条件.写出对应的增广矩阵以便行化简求平衡价格.
c. [M] 找出当机器部门产出的价格是100个单位时的一组平衡价格
解答 :
a. 交易表(按列填写,每列之和为1)
| 采购部门 | 化学金属 | 燃料动力 | 机器 |
|---|---|---|---|
| 化学金属 | 0.2 | 0.8 | 0.4 |
| 燃料动力 | 0.3 | 0.1 | 0.4 |
| 机器 | 0.5 | 0.1 | 0.2 |
b. 设 pC,pF,pMp_C, p_F, p_MpC,pF,pM 为各部门总产出
化学金属部门:pC=0.2pC+0.8pF+0.4pMp_C = 0.2p_C + 0.8p_F + 0.4p_MpC=0.2pC+0.8pF+0.4pM
燃料动力部门:pF=0.3pC+0.1pF+0.4pMp_F = 0.3p_C + 0.1p_F + 0.4p_MpF=0.3pC+0.1pF+0.4pM
机器部门:pM=0.5pC+0.1pF+0.2pMp_M = 0.5p_C + 0.1p_F + 0.2p_MpM=0.5pC+0.1pF+0.2pM
移项得:
{0.8pC−0.8pF−0.4pM=0−0.3pC+0.9pF−0.4pM=0−0.5pC−0.1pF+0.8pM=0 \begin{cases} 0.8p_C - 0.8p_F - 0.4p_M = 0 \\ -0.3p_C + 0.9p_F - 0.4p_M = 0 \\ -0.5p_C - 0.1p_F + 0.8p_M = 0 \end{cases} ⎩ ⎨ ⎧0.8pC−0.8pF−0.4pM=0−0.3pC+0.9pF−0.4pM=0−0.5pC−0.1pF+0.8pM=0
增广矩阵(每行乘以10简化):
8−8−40−39−40−5−180\] \\begin{bmatrix} 8 \& -8 \& -4 \& 0 \\\\ -3 \& 9 \& -4 \& 0 \\\\ -5 \& -1 \& 8 \& 0 \\end{bmatrix} 8−3−5−89−1−4−48000 **c. 行化简得** :pC=1.417pM, pF=0.917pMp_C = 1.417p_M,\\ p_F = 0.917p_MpC=1.417pM, pF=0.917pM,pMp_MpM 自由。 当 pM=100p_M = 100pM=100 时,pC=141.7, pF=91.7p_C = 141.7,\\ p_F = 91.7pC=141.7, pF=91.7。 **结论** : a. 交易表如上; b. 方程组及增广矩阵如上; c. 一组平衡价格为 pM=100, pC≈141.7, pF≈91.7p_M = 100,\\ p_C \\approx 141.7,\\ p_F \\approx 91.7pM=100, pC≈141.7, pF≈91.7。只有价格比例确定,经济均衡不受货币单位影响。 *** ** * ** *** > 5. 硫化硼与水剧烈反应生成硼酸和硫化氢气体(臭蛋味).未配平的化学反应式为 > B2S3+H2O→H3BO3+H2S\\text{B}_2\\text{S}_3 + \\text{H}_2\\text{O} \\rightarrow \\text{H}_3\\text{BO}_3 + \\text{H}_2\\text{S}B2S3+H2O→H3BO3+H2S **解答** : 对每个化合物构建原子向量(硼、硫、氢、氧): B2S3:\[2300\], H2O:\[0021\], H3BO3:\[1033\], H2S:\[0120\]\\text{B}_2\\text{S}_3: \\begin{bmatrix}2\\\\3\\\\0\\\\0\\end{bmatrix},\\ \\text{H}_2\\text{O}: \\begin{bmatrix}0\\\\0\\\\2\\\\1\\end{bmatrix},\\ \\text{H}_3\\text{BO}_3: \\begin{bmatrix}1\\\\0\\\\3\\\\3\\end{bmatrix},\\ \\text{H}_2\\text{S}: \\begin{bmatrix}0\\\\1\\\\2\\\\0\\end{bmatrix}B2S3: 2300 , H2O: 0021 , H3BO3: 1033 , H2S: 0120 设配平系数为 x1,x2,x3,x4x_1, x_2, x_3, x_4x1,x2,x3,x4,满足: x1\[2300\]+x2\[0021\]=x3\[1033\]+x4\[0120\] x_1\\begin{bmatrix}2\\\\3\\\\0\\\\0\\end{bmatrix} + x_2\\begin{bmatrix}0\\\\0\\\\2\\\\1\\end{bmatrix} = x_3\\begin{bmatrix}1\\\\0\\\\3\\\\3\\end{bmatrix} + x_4\\begin{bmatrix}0\\\\1\\\\2\\\\0\\end{bmatrix} x1 2300 +x2 0021 =x3 1033 +x4 0120 移项并化简增广矩阵: \[20−100300−1002−3−2001−300\]→⋯→\[100−130010−20001−23000000\] \\begin{bmatrix} 2 \& 0 \& -1 \& 0 \& 0 \\\\ 3 \& 0 \& 0 \& -1 \& 0 \\\\ 0 \& 2 \& -3 \& -2 \& 0 \\\\ 0 \& 1 \& -3 \& 0 \& 0 \\end{bmatrix} \\rightarrow \\cdots \\rightarrow \\begin{bmatrix} 1 \& 0 \& 0 \& -\\frac{1}{3} \& 0 \\\\ 0 \& 1 \& 0 \& -2 \& 0 \\\\ 0 \& 0 \& 1 \& -\\frac{2}{3} \& 0 \\\\ 0 \& 0 \& 0 \& 0 \& 0 \\end{bmatrix} 23000021−10−3−30−1−200000 →⋯→ 100001000010−31−2−3200000 通解:x1=13x4, x2=2x4, x3=23x4x_1 = \\frac{1}{3}x_4,\\ x_2 = 2x_4,\\ x_3 = \\frac{2}{3}x_4x1=31x4, x2=2x4, x3=32x4,x4x_4x4 自由。 取 x4=3x_4 = 3x4=3,则 x1=1, x2=6, x3=2x_1 = 1,\\ x_2 = 6,\\ x_3 = 2x1=1, x2=6, x3=2。 **结论** : 配平后的方程式为 B2S3+6H2O→2H3BO3+3H2S\\text{B}_2\\text{S}_3 + 6\\text{H}_2\\text{O} \\rightarrow 2\\text{H}_3\\text{BO}_3 + 3\\text{H}_2\\text{S}B2S3+6H2O→2H3BO3+3H2S *** ** * ** *** > 6. 磷酸钠和硝酸钡反应生成磷酸钡和硝酸钠的未配平方程式为 > Na3PO4+Ba(NO3)2→Ba3(PO4)2+NaNO3\\text{Na}_3\\text{PO}_4 + \\text{Ba}(\\text{NO}_3)_2 \\rightarrow \\text{Ba}_3(\\text{PO}_4)_2 + \\text{NaNO}_3Na3PO4+Ba(NO3)2→Ba3(PO4)2+NaNO3 **解答** : 对每个化合物构建原子向量(钠、磷、氧、钡、氮): Na3PO4:\[31400\], Ba(NO3)2:\[00612\], Ba3(PO4)2:\[02830\], NaNO3:\[10301\]\\text{Na}_3\\text{PO}_4: \\begin{bmatrix}3\\\\1\\\\4\\\\0\\\\0\\end{bmatrix},\\ \\text{Ba}(\\text{NO}_3)_2: \\begin{bmatrix}0\\\\0\\\\6\\\\1\\\\2\\end{bmatrix},\\ \\text{Ba}_3(\\text{PO}_4)_2: \\begin{bmatrix}0\\\\2\\\\8\\\\3\\\\0\\end{bmatrix},\\ \\text{NaNO}_3: \\begin{bmatrix}1\\\\0\\\\3\\\\0\\\\1\\end{bmatrix}Na3PO4: 31400 , Ba(NO3)2: 00612 , Ba3(PO4)2: 02830 , NaNO3: 10301 设系数为 x1,x2,x3,x4x_1, x_2, x_3, x_4x1,x2,x3,x4,满足向量方程并移项化简增广矩阵: \[300−1010−20046−8−3001−300020−10\]→⋯→\[100−130010−120001−16000000\] \\begin{bmatrix} 3 \& 0 \& 0 \& -1 \& 0 \\\\ 1 \& 0 \& -2 \& 0 \& 0 \\\\ 4 \& 6 \& -8 \& -3 \& 0 \\\\ 0 \& 1 \& -3 \& 0 \& 0 \\\\ 0 \& 2 \& 0 \& -1 \& 0 \\end{bmatrix} \\rightarrow \\cdots \\rightarrow \\begin{bmatrix} 1 \& 0 \& 0 \& -\\frac{1}{3} \& 0 \\\\ 0 \& 1 \& 0 \& -\\frac{1}{2} \& 0 \\\\ 0 \& 0 \& 1 \& -\\frac{1}{6} \& 0 \\\\ 0 \& 0 \& 0 \& 0 \& 0 \\end{bmatrix} 31400006120−2−8−30−10−30−100000 →⋯→ 100001000010−31−21−6100000 通解:x1=13x4, x2=12x4, x3=16x4x_1 = \\frac{1}{3}x_4,\\ x_2 = \\frac{1}{2}x_4,\\ x_3 = \\frac{1}{6}x_4x1=31x4, x2=21x4, x3=61x4,x4x_4x4 自由。 取 x4=6x_4 = 6x4=6,得 x1=2, x2=3, x3=1x_1 = 2,\\ x_2 = 3,\\ x_3 = 1x1=2, x2=3, x3=1。 **结论** : 配平后的方程式为 2Na3PO4+3Ba(NO3)2→Ba3(PO4)2+6NaNO32\\text{Na}_3\\text{PO}_4 + 3\\text{Ba}(\\text{NO}_3)_2 \\rightarrow \\text{Ba}_3(\\text{PO}_4)_2 + 6\\text{NaNO}_32Na3PO4+3Ba(NO3)2→Ba3(PO4)2+6NaNO3 *** ** * ** *** > **7. Alka-Seltzer碱性苏打包含碳酸氢钠(NaHCO3\\text{NaHCO}_3NaHCO3)和柠檬酸(H3C6H5O7\\text{H}_3\\text{C}_6\\text{H}_5\\text{O}_7H3C6H5O7).当一颗药片溶解在水中时,会发生化学反应生成柠檬酸钠、水和二氧化碳的反应为** > NaHCO3+H3C6H5O7→Na3C6H5O7+H2O+CO2\\text{NaHCO}_3 + \\text{H}_3\\text{C}_6\\text{H}_5\\text{O}_7 \\rightarrow \\text{Na}_3\\text{C}_6\\text{H}_5\\text{O}_7 + \\text{H}_2\\text{O} + \\text{CO}_2NaHCO3+H3C6H5O7→Na3C6H5O7+H2O+CO2 **解答** : 按原子出现顺序构建向量(钠、氢、碳、氧): NaHCO3:\[1113\], H3C6H5O7:\[0867\], Na3C6H5O7:\[3567\], H2O:\[0201\], CO2:\[0012\]\\text{NaHCO}_3: \\begin{bmatrix}1\\\\1\\\\1\\\\3\\end{bmatrix},\\ \\text{H}_3\\text{C}_6\\text{H}_5\\text{O}_7: \\begin{bmatrix}0\\\\8\\\\6\\\\7\\end{bmatrix},\\ \\text{Na}_3\\text{C}_6\\text{H}_5\\text{O}_7: \\begin{bmatrix}3\\\\5\\\\6\\\\7\\end{bmatrix},\\ \\text{H}_2\\text{O}: \\begin{bmatrix}0\\\\2\\\\0\\\\1\\end{bmatrix},\\ \\text{CO}_2: \\begin{bmatrix}0\\\\0\\\\1\\\\2\\end{bmatrix}NaHCO3: 1113 , H3C6H5O7: 0867 , Na3C6H5O7: 3567 , H2O: 0201 , CO2: 0012 设系数为 x1,x2,x3,x4,x5x_1, x_2, x_3, x_4, x_5x1,x2,x3,x4,x5,满足向量方程并移项化简: \[10−300018−5−20016−60−1037−7−1−20\]→⋯→\[1000−100100−1300010−1300001−10\] \\begin{bmatrix} 1 \& 0 \& -3 \& 0 \& 0 \& 0 \\\\ 1 \& 8 \& -5 \& -2 \& 0 \& 0 \\\\ 1 \& 6 \& -6 \& 0 \& -1 \& 0 \\\\ 3 \& 7 \& -7 \& -1 \& -2 \& 0 \\end{bmatrix} \\rightarrow \\cdots \\rightarrow \\begin{bmatrix} 1 \& 0 \& 0 \& 0 \& -1 \& 0 \\\\ 0 \& 1 \& 0 \& 0 \& -\\frac{1}{3} \& 0 \\\\ 0 \& 0 \& 1 \& 0 \& -\\frac{1}{3} \& 0 \\\\ 0 \& 0 \& 0 \& 1 \& -1 \& 0 \\end{bmatrix} 11130867−3−5−6−70−20−100−1−20000 →⋯→ 1000010000100001−1−31−31−10000 通解:x1=x5, x2=13x5, x3=13x5, x4=x5x_1 = x_5,\\ x_2 = \\frac{1}{3}x_5,\\ x_3 = \\frac{1}{3}x_5,\\ x_4 = x_5x1=x5, x2=31x5, x3=31x5, x4=x5,x5x_5x5 自由。 取 x5=3x_5 = 3x5=3,得 x1=x4=3, x2=x3=1x_1 = x_4 = 3,\\ x_2 = x_3 = 1x1=x4=3, x2=x3=1。 **结论** : 配平后的方程式为 3NaHCO3+H3C6H5O7→Na3C6H5O7+3H2O+3CO23\\text{NaHCO}_3 + \\text{H}_3\\text{C}_6\\text{H}_5\\text{O}_7 \\rightarrow \\text{Na}_3\\text{C}_6\\text{H}_5\\text{O}_7 + 3\\text{H}_2\\text{O} + 3\\text{CO}_23NaHCO3+H3C6H5O7→Na3C6H5O7+3H2O+3CO2 *** ** * ** *** > **8. 高锰酸钾和硫酸锰在水中反应生成二氧化锰、硫酸钾和硫酸的反应为** > KMnO4+MnSO4+H2O→MnO2+K2SO4+H2SO4\\text{KMnO}_4 + \\text{MnSO}_4 + \\text{H}_2\\text{O} \\rightarrow \\text{MnO}_2 + \\text{K}_2\\text{SO}_4 + \\text{H}_2\\text{SO}_4KMnO4+MnSO4+H2O→MnO2+K2SO4+H2SO4 **解答** : 构建原子向量(钾、锰、氧、硫、氢): KMnO4:\[11400\], MnSO4:\[01410\], H2O:\[00102\], MnO2:\[01200\], K2SO4:\[20410\], H2SO4:\[00412\]\\text{KMnO}_4: \\begin{bmatrix}1\\\\1\\\\4\\\\0\\\\0\\end{bmatrix},\\ \\text{MnSO}_4: \\begin{bmatrix}0\\\\1\\\\4\\\\1\\\\0\\end{bmatrix},\\ \\text{H}_2\\text{O}: \\begin{bmatrix}0\\\\0\\\\1\\\\0\\\\2\\end{bmatrix},\\ \\text{MnO}_2: \\begin{bmatrix}0\\\\1\\\\2\\\\0\\\\0\\end{bmatrix},\\ \\text{K}_2\\text{SO}_4: \\begin{bmatrix}2\\\\0\\\\4\\\\1\\\\0\\end{bmatrix},\\ \\text{H}_2\\text{SO}_4: \\begin{bmatrix}0\\\\0\\\\4\\\\1\\\\2\\end{bmatrix}KMnO4: 11400 , MnSO4: 01410 , H2O: 00102 , MnO2: 01200 , K2SO4: 20410 , H2SO4: 00412 设系数为 x1,x2,x3,x4,x5,x6x_1, x_2, x_3, x_4, x_5, x_6x1,x2,x3,x4,x5,x6,满足向量方程并移项化简: \[1000−200110−1000441−2−4−400100−1−1000200−20\]→⋯→\[10000−1001000−1.5000100−1000010−2.5000001−0.50\] \\begin{bmatrix} 1 \& 0 \& 0 \& 0 \& -2 \& 0 \& 0 \\\\ 1 \& 1 \& 0 \& -1 \& 0 \& 0 \& 0 \\\\ 4 \& 4 \& 1 \& -2 \& -4 \& -4 \& 0 \\\\ 0 \& 1 \& 0 \& 0 \& -1 \& -1 \& 0 \\\\ 0 \& 0 \& 2 \& 0 \& 0 \& -2 \& 0 \\end{bmatrix} \\rightarrow \\cdots \\rightarrow \\begin{bmatrix} 1 \& 0 \& 0 \& 0 \& 0 \& -1 \& 0 \\\\ 0 \& 1 \& 0 \& 0 \& 0 \& -1.5 \& 0 \\\\ 0 \& 0 \& 1 \& 0 \& 0 \& -1 \& 0 \\\\ 0 \& 0 \& 0 \& 1 \& 0 \& -2.5 \& 0 \\\\ 0 \& 0 \& 0 \& 0 \& 1 \& -0.5 \& 0 \\end{bmatrix} 1140001410001020−1−200−20−4−1000−4−1−200000 →⋯→ 1000001000001000001000001−1−1.5−1−2.5−0.500000 通解:x1=x6, x2=1.5x6, x3=x6, x4=2.5x6, x5=0.5x6x_1 = x_6,\\ x_2 = 1.5x_6,\\ x_3 = x_6,\\ x_4 = 2.5x_6,\\ x_5 = 0.5x_6x1=x6, x2=1.5x6, x3=x6, x4=2.5x6, x5=0.5x6,x6x_6x6 自由。 取 x6=2x_6 = 2x6=2,得 x1=x3=2, x2=3, x4=5, x5=1x_1 = x_3 = 2,\\ x_2 = 3,\\ x_4 = 5,\\ x_5 = 1x1=x3=2, x2=3, x4=5, x5=1。 **结论** : 配平后的方程式为 2KMnO4+3MnSO4+2H2O→5MnO2+K2SO4+2H2SO42\\text{KMnO}_4 + 3\\text{MnSO}_4 + 2\\text{H}_2\\text{O} \\rightarrow 5\\text{MnO}_2 + \\text{K}_2\\text{SO}_4 + 2\\text{H}_2\\text{SO}_42KMnO4+3MnSO4+2H2O→5MnO2+K2SO4+2H2SO4 *** ** * ** *** > **9. \[M\] 如果可能,使用精确的算术或合理的计算格式配平如下的化学反应方程式:** > PbN6+CrMn2O8→Pb3O4+Cr2O3+MnO2+NO\\text{PbN}_6 + \\text{CrMn}_2\\text{O}_8 \\rightarrow \\text{Pb}_3\\text{O}_4 + \\text{Cr}_2\\text{O}_3 + \\text{MnO}_2 + \\text{NO}PbN6+CrMn2O8→Pb3O4+Cr2O3+MnO2+NO **解答** : 构建原子向量(铅、氮、铬、锰、氧): PbN6:\[16000\], CrMn2O8:\[00128\], Pb3O4:\[30004\], Cr2O3:\[00203\], MnO2:\[00012\], NO:\[01001\]\\text{PbN}_6: \\begin{bmatrix}1\\\\6\\\\0\\\\0\\\\0\\end{bmatrix},\\ \\text{CrMn}_2\\text{O}_8: \\begin{bmatrix}0\\\\0\\\\1\\\\2\\\\8\\end{bmatrix},\\ \\text{Pb}_3\\text{O}_4: \\begin{bmatrix}3\\\\0\\\\0\\\\0\\\\4\\end{bmatrix},\\ \\text{Cr}_2\\text{O}_3: \\begin{bmatrix}0\\\\0\\\\2\\\\0\\\\3\\end{bmatrix},\\ \\text{MnO}_2: \\begin{bmatrix}0\\\\0\\\\0\\\\1\\\\2\\end{bmatrix},\\ \\text{NO}: \\begin{bmatrix}0\\\\1\\\\0\\\\0\\\\1\\end{bmatrix}PbN6: 16000 , CrMn2O8: 00128 , Pb3O4: 30004 , Cr2O3: 00203 , MnO2: 00012 , NO: 01001 设系数为 x1,x2,x3,x4,x5,x6x_1, x_2, x_3, x_4, x_5, x_6x1,x2,x3,x4,x5,x6,满足向量方程并移项化简: \[10−3000060000−10010−20000200−10008−4−3−2−10\]→⋯→\[10000−16001000−2245000100−118000010−1145000001−44450\] \\begin{bmatrix} 1 \& 0 \& -3 \& 0 \& 0 \& 0 \& 0 \\\\ 6 \& 0 \& 0 \& 0 \& 0 \& -1 \& 0 \\\\ 0 \& 1 \& 0 \& -2 \& 0 \& 0 \& 0 \\\\ 0 \& 2 \& 0 \& 0 \& -1 \& 0 \& 0 \\\\ 0 \& 8 \& -4 \& -3 \& -2 \& -1 \& 0 \\end{bmatrix} \\rightarrow \\cdots \\rightarrow \\begin{bmatrix} 1 \& 0 \& 0 \& 0 \& 0 \& -\\frac{1}{6} \& 0 \\\\ 0 \& 1 \& 0 \& 0 \& 0 \& -\\frac{22}{45} \& 0 \\\\ 0 \& 0 \& 1 \& 0 \& 0 \& -\\frac{1}{18} \& 0 \\\\ 0 \& 0 \& 0 \& 1 \& 0 \& -\\frac{11}{45} \& 0 \\\\ 0 \& 0 \& 0 \& 0 \& 1 \& -\\frac{44}{45} \& 0 \\end{bmatrix} 1600000128−3000−400−20−3000−1−20−100−100000 →⋯→ 1000001000001000001000001−61−4522−181−4511−454400000 通解:x1=16x6, x2=2245x6, x3=118x6, x4=1145x6, x5=4445x6x_1 = \\frac{1}{6}x_6,\\ x_2 = \\frac{22}{45}x_6,\\ x_3 = \\frac{1}{18}x_6,\\ x_4 = \\frac{11}{45}x_6,\\ x_5 = \\frac{44}{45}x_6x1=61x6, x2=4522x6, x3=181x6, x4=4511x6, x5=4544x6,x6x_6x6 自由。 取 x6=90x_6 = 90x6=90,得 x1=15, x2=44, x3=5, x4=22, x5=88x_1 = 15,\\ x_2 = 44,\\ x_3 = 5,\\ x_4 = 22,\\ x_5 = 88x1=15, x2=44, x3=5, x4=22, x5=88。 **结论** : 配平后的方程式为 15PbN6+44CrMn2O8→5Pb3O4+22Cr2O3+88MnO2+90NO15\\text{PbN}_6 + 44\\text{CrMn}_2\\text{O}_8 \\rightarrow 5\\text{Pb}_3\\text{O}_4 + 22\\text{Cr}_2\\text{O}_3 + 88\\text{MnO}_2 + 90\\text{NO}15PbN6+44CrMn2O8→5Pb3O4+22Cr2O3+88MnO2+90NO *** ** * ** *** > **11. 求下图中网络流量的通解.假设流量都是非负的,x5x_5x5 可能的最大值是什么?** 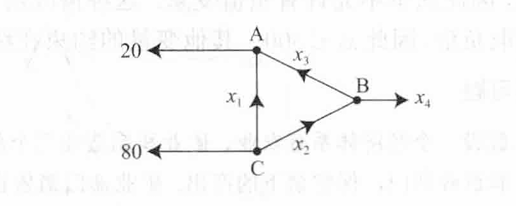 **解答** : 写出各节点方程: | 节点 | 流入 | 流出 | |----|---------------------|---------------------| | A | x1+x3x_1 + x_3x1+x3 | 20 | | B | x2x_2x2 | x3+x4x_3 + x_4x3+x4 | | C | 80 | x1+x2x_1 + x_2x1+x2 | | 总计 | 80 | x4+20x_4 + 20x4+20 | 整理得: {x1+x3=20x2−x3−x4=0x1+x2=80x4=60 \\begin{cases} x_1 + x_3 = 20 \\\\ x_2 - x_3 - x_4 = 0 \\\\ x_1 + x_2 = 80 \\\\ x_4 = 60 \\end{cases} ⎩ ⎨ ⎧x1+x3=20x2−x3−x4=0x1+x2=80x4=60 增广矩阵化简: \[10102001−1−10110080000160\]→\[10102001−106000016000000\] \\begin{bmatrix} 1 \& 0 \& 1 \& 0 \& 20 \\\\ 0 \& 1 \& -1 \& -1 \& 0 \\\\ 1 \& 1 \& 0 \& 0 \& 80 \\\\ 0 \& 0 \& 0 \& 1 \& 60 \\end{bmatrix} \\rightarrow \\begin{bmatrix} 1 \& 0 \& 1 \& 0 \& 20 \\\\ 0 \& 1 \& -1 \& 0 \& 60 \\\\ 0 \& 0 \& 0 \& 1 \& 60 \\\\ 0 \& 0 \& 0 \& 0 \& 0 \\end{bmatrix} 101001101−1000−1012008060 → 100001001−10000102060600 通解: {x1=20−x3x2=60+x3x3是自由变量x4=60 \\begin{cases} x_1 = 20 - x_3 \\\\ x_2 = 60 + x_3 \\\\ x_3 是自由变量 \\\\ x_4 = 60 \\end{cases} ⎩ ⎨ ⎧x1=20−x3x2=60+x3x3是自由变量x4=60 因为非负 所以 x3x_3x3 最大是20