第一部分:核心概念与定义
导数 描述的是函数在某一点处的瞬时变化率,即函数值随自变量变化的快慢。
数学定义(极限定义):对于函数 y=f(x)y=f(x),在点 xx 处的导数定义为:
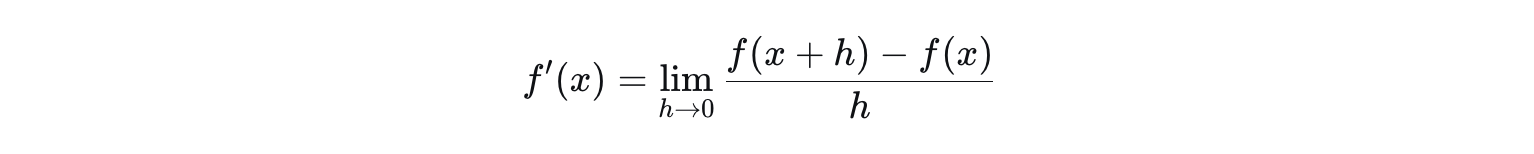
这个公式可以理解为"平均变化率"在两点无限接近时的极限。
第二部分:计算公式与法则
在实际计算中,我们通常使用一系列推导好的公式和法则,而非每次都使用极限定义。
-
基本初等函数导数公式
这是计算的基石。

-
导数的运算法则
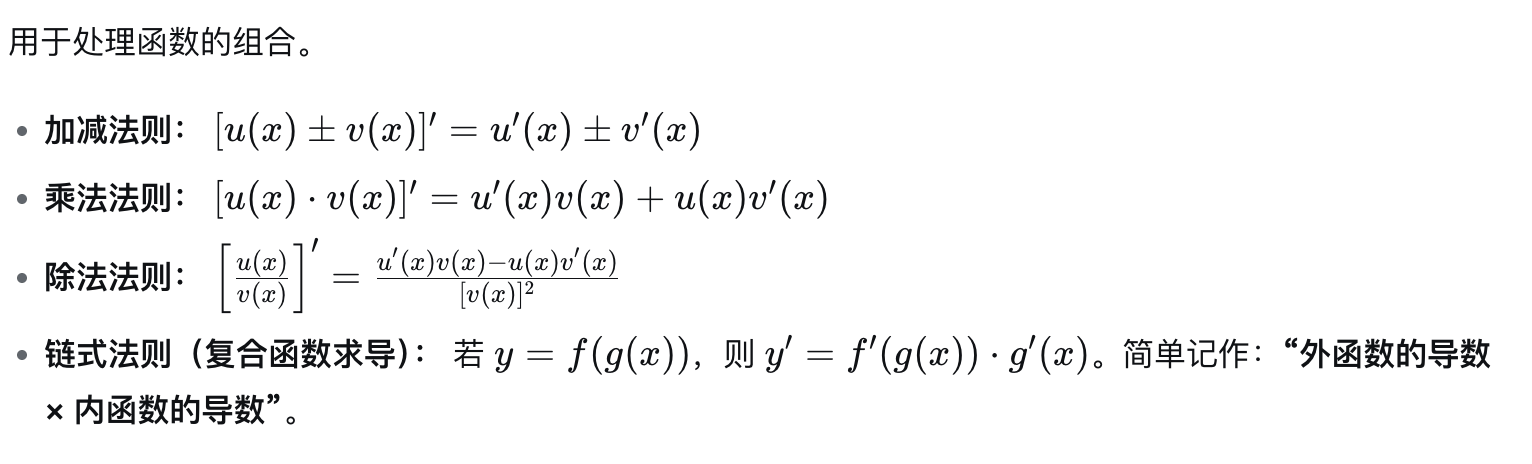
第三部分:数据与计算示例


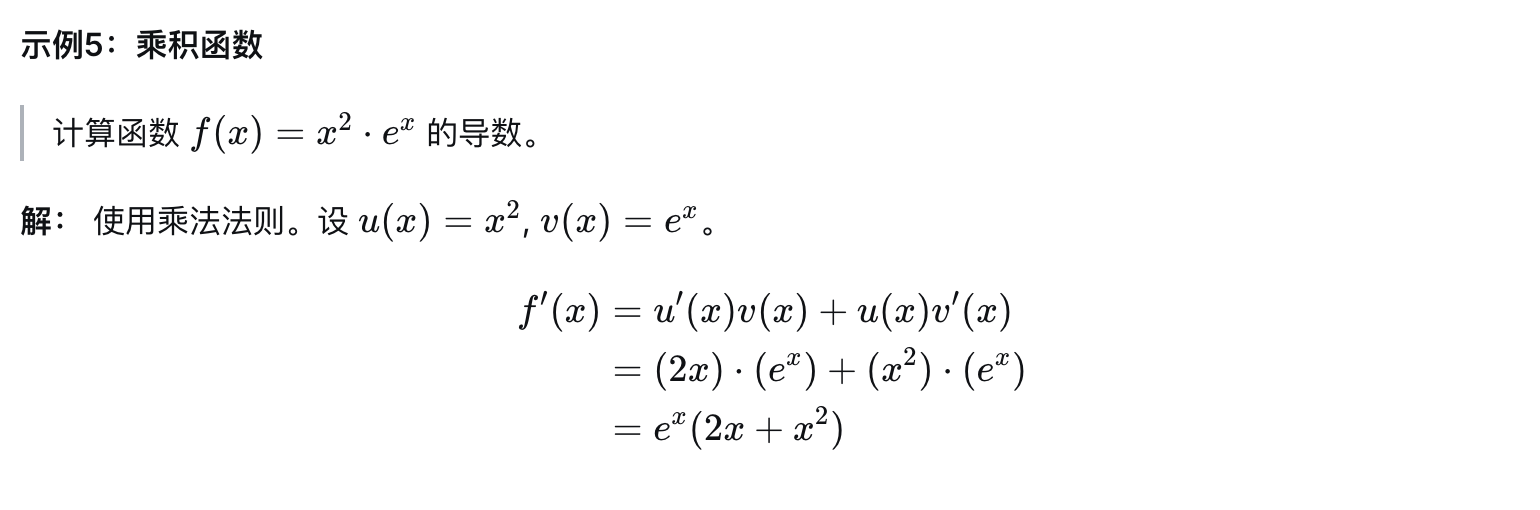
第四部分:导数的应用意义(数据解读)

总结

要熟练计算导数,关键在于:
- 牢记基本公式。
- 识别函数结构(是乘积、商还是复合)。
- 正确对应法则,逐步计算。
从这些基础出发,你可以计算绝大多数初等函数的导数。