目录
[2.4 数据获取接口 at,operator[ ]](#2.4 数据获取接口 at,operator[ ])
[4.initializer_list { } 与 隐式类型转换,迭代器访问](#4.initializer_list { } 与 隐式类型转换,迭代器访问)
[5.emplace_back 和 push_back 的差异](#5.emplace_back 和 push_back 的差异)
1.vector的构造函数
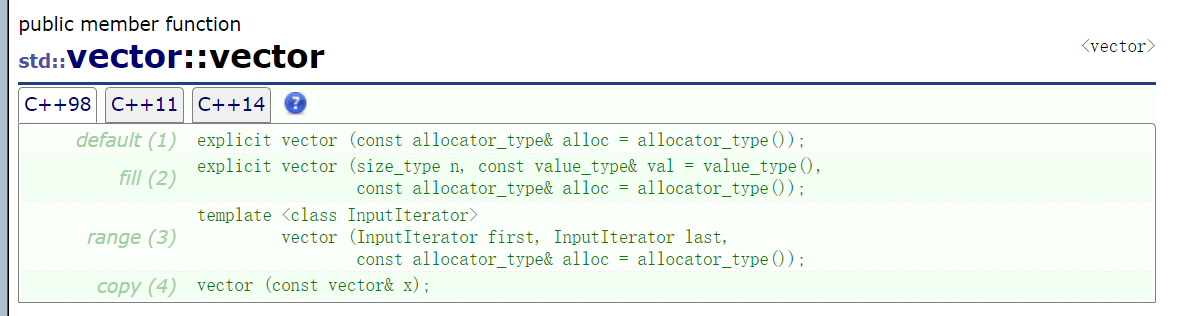
(1) 构造函数的参数是内存池,我们日常不需要理会,除非你要用自己的内存池,这就是默认构造,explicit修饰,说明该函数不支持隐式类型转换。
(2)用 n 个 val 构造对象
(3)用迭代器区间构造对象,不一定是自己的迭代器,可以类型转换的也行
(4)拷贝构造
//插入10个数据,都是1
vector<int> v1(10, 1);
//默认构造
vector<int> v2;
//拷贝构造
vector<int> v3(v1);
//迭代器区间构造
vector<int> v4(v1.begin(), v1.end());
//也可以用别的容器的迭代器,前提是支持类型转换的
string s1("xxxxxxxxxxx");
//string迭代器内容是char的,其ASCII码值是int,所以可以类型转换
//并且,char转int不用考虑数据溢出风险,小转大不会溢出。
vector<int> v5(s1.begin(), s1.end());注意最后一个注释
这里再讲解一个 C++11 添加的非常实用的构造:

花括号 { } 是 initializer_list 类型,C++11定义的新参数 ,其实string也有,不过没用处,十分麻烦,所以没之前介绍
//vector<int> v6({ 1,2,3,4,5,6,7,8,9,10 });
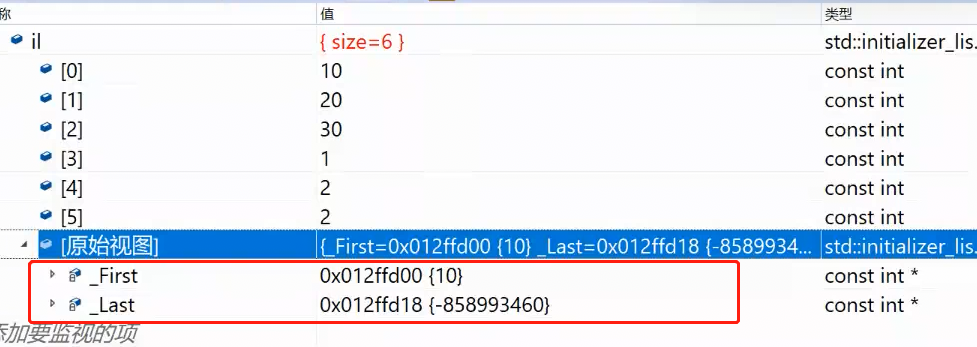
vector<int> v7 = { 1,2,3,4,5,6,7,8,9,10 };如图,编译器优化为直接构造(原本是隐式类型转换构造了一个vector对象),严格来说是上面那样,拷贝构造的写法,不过都可以。
有了initializer_list,可以让它像数组一样初始化。
它的底层原理就是两个指针 :把括号内的数据存在临时数组,然后提供了指向首位置和尾下一个位置的指针(迭代器)
所以它是可以使用 范围for 的:

2.迭代器以及各种简单接口:
2.1迭代器

vector的迭代器是和string一样的,用法就是那样
2.2capacity简单接口

是不是十分熟悉?是的,大部分在 string 中都有,使用方式也一样,都是成员函数,利用vector对象就能随手调用
2.3operator=

operator= 十分好用,所以单独拿出来讲,不过它的使用也十分简单,(2)涉及更难的知识,目前不需要知道。
只需要记住:赋值是针对于 已存在对象的操作 (3)的initializer_list 类型也是针对已存在对象,不要与构造函数混淆
vector<int> v1={1,2,3,4,5}
vector<int> v2;
//v2先存在,才能谈赋值。
v2 = v1;
//一样,这才是赋值,不要与第一行的构造混淆
v2={1,0,0,8,6};2.4 数据获取接口 at,operator[ ]
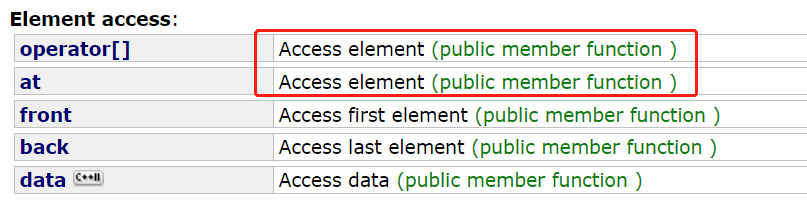
这部分和string也是一样。甚至用法也一样。 也只需要知道前两个。 再次提醒:
at和[ ] 都会检测是否越界,不过:at 抛异常,不中止程序,[ ] 是严格的 断言检查,直接中止程序。 (在Debug下)
3.vector的增删查改

主要了解这部分的使用
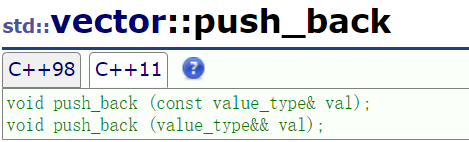
3.1push_back
尾插没什么区别,参数都是 一个值 val
3.2pop_back
这个没参数,直接调用函数实现 尾删

3.3insert
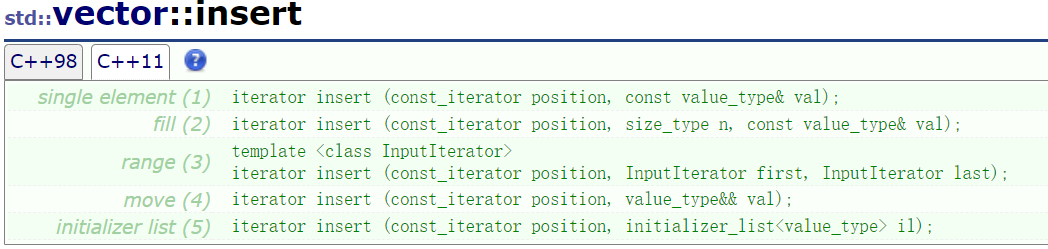
这里的insert参数都是用迭代器iterator 实现的,第一个最常用,我们了解第一个就行
//头插 ,头删, 指定位置插入或者删除
v1.insert(v1.begin(), 0);
v1.insert(v1.begin()+3, 1);迭代器参数可以是表达式形式
3.4erase
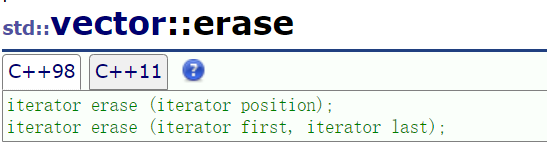
(1)删除pos迭代器位置 (2)删除一段迭代器区间
最常用的是(1):删除pos迭代器位置
v1.erase(v1.begin());
v1.erase(v1.begin()+3);迭代器可以是表达式形式
3.5clear
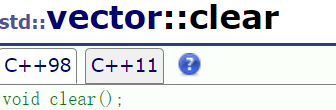
清理数据,不清空间,和string一样
4.initializer_list { } 与 隐式类型转换,迭代器访问
我们构造一个struct AA:
//也是类 ,但默认为public
struct AA
{
int _a1 = 1;
int _a2 = 1;
AA(int a1, int a2)
:_a1(a1)
,_a2(a2)
{}
};这是一个类,struct也是类,不过成员默认为public 我们可以这样:
AA aa1 = { 0,0 };
AA aa2({ 0,0 });这就是多参数的隐式类型转换,构造了AA对象 ,两种写法都行
那如果我们定义了一个存储AA的vector(vector<AA>)就可以这样:
//隐式类型转换
vector<AA> v1 = { {1,1},{2,2},{3,3} };
//也可以一部分是AA对象
vector<AA> v1 = { aa1,{1,1},{2,2},{3,3} };这就是两者的结合,可以避免繁琐地一个个创建AA对象,直接用隐式类型转换,vector构造更方便
4.1迭代器访问
当利用迭代器遍历 vector<AA> 时,若AA并没有支持流插入 cout,所以无法完成遍历:
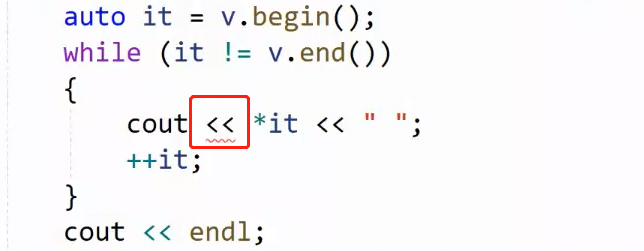
此时有两种办法:1. 重载 << 运算符,让AA支持 cout 输出
- 让迭代器用 -> 访问AA对象的成员(public):
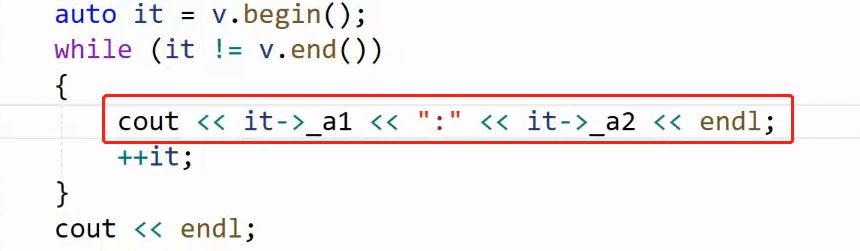
为什么迭代器it可以访问类的成员?
已知vector的迭代器是指针的封装。vector底层是个数组,存储AA对象,迭代器指向数组内容,也就是指向AA对象,那这个指针就是 AA* 指针,AA* 指针就可以访问AA内部的公有成员。
5.emplace_back 和 push_back 的差异
emplace_back 和 push_back 作用基本相同 但也有差异。我们衔接 4. 的内容来理解:
//push_back 和 emplace_back 用法差不多
v1.push_back(aa1);
v1.emplace_back(aa1);它们都可以插入一个值 , 但是emplace_back :
//可以直接传构造AA的参数,因为他是可变参数模板(现阶段没学)
//更高效,会直接构造AA
v1.emplace_back(1, 1);push_back:
//只能传AA对象,不能穿构造AA的参数,这就是区别
//{1,1} 也是AA对象,因为隐式类型转换,构造临时对象AA
v1.push_back({ 1,1 });这就是区别 ,有时候emplace_back 更高效。注意,这两个写法不能交叉用,都是各自专属
6.非成员函数:vector中比较大下的函数
不是成员函数,而是全局的函数模板

当然少不了比较大小的函数,用处比较少,了解即可
优先比较 size,其次从前往后比较数据大小,返回bool值。
7.杨辉三角实现-理解二维vector(二维数组)
vector一维数组已经基本掌握了,那二维数组呢? 用一道题来理解它:杨辉三角
7.1二维vector的理解(二维数组)
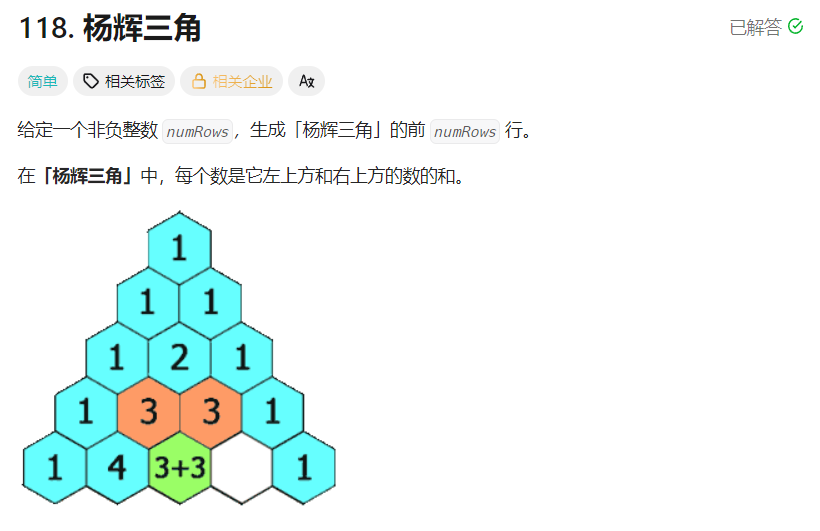
它给了我们这个接口:vector<vector<int>> 这代表什么?vector 里 存放着 vector<int>,也就是数组的每个元素都是整型数组
这就是二维数组。

如图,那么首先,vector的类模板就会实例化两个模板类,首先是vector<int>类型,,然后是vector<vector<int>>类型
遵循从里到外的顺序实例化
前者底层指针为int*类型(如图右上), 该指针指向一片存储int的数组
后者的底层指针为vector<int>* 类型(如图右下),该指针指向一片存储vector<int>的空间------每个元素都是一个vector<int>对象,
每个对象底层都管理一片整型数组。
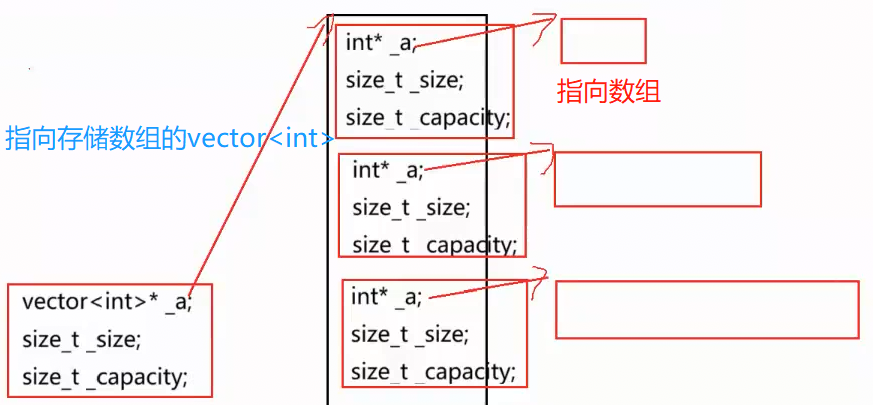
如图所示,十分直观。 外层数组存储vector<int>,行数,内层数组存储整型数组,列数。
有个疑问,题目的图中是等腰三角形,我们这样展现的"杨辉三角"不就是直角三角形了吗?
我们实现的"直角三角形",其实错位一下就能变成"等腰三角形",只是视觉上的不一样,实际上是等价的:
1 1
12 12 如左边,显而易见,是等价的。
123 123
7.2题目解析
理解后,我们开始理清思路,然后一步步实现代码:
杨辉三角,根据图发现:每行的第一个和最后一个元素都是1 ,然后第一行和第二行都是 1
然后每行中间的元素比如i 行 j 列 的元素 的值 = i-1 行 j 列 的值 +i-1 行 j-1 列 的值
知道了这些后,就只需要实现一个二维vector就行
思路:先创建一个二维数组,然后分别初始化它外层存放vector<int>的,然后初始化内层存放整型数组的
外层初始化为匿名对象,这样可以避免繁琐的构造,更方便,内层全初始化为1,利用resize,因为很多地方都是1,这样只需要对杨辉三角内部值进行修改。
代码实现演示:
也是直接通过了
class Solution {
public:
vector<vector<int>> generate(int numRows)
{
vector<vector<int>> vv;
//初始化行:利用resize,都初始化为匿名对象
vv.resize(numRows,vector<int>());
//初始化列:
for(size_t i = 0;i<numRows;i++)
{
//第0行有1个元素,第1行2个,第i行i+1个,全初始化为1
//vv[i]就是第几行的vector<int>,初始化它对应的数组,注意,别搞错了
vv[i].resize(i+1,1);
}
//初始化完后,开始修改值:
//0,1行都是1,不需要是修改
for(size_t i = 2; i<numRows; i++)
{
//0,和vv[i].szie()-1位置都是1,不需要修改
for(size_t j=1; j<vv[i].size()-1; j++)
{
vv[i][j]=vv[i-1][j]+vv[i-1][j-1];
}
}
return vv;
}
};到这,就稍微理解了二维vector(二维数组)了。
感谢支持!