扩展
物理应用
力矩 角动量 洛伦兹力 线速度与角速度
三维叉乘的公式
( ⃗ x 1 , y 1 , z 1 ) × ( ⃗ x 2 , y 2 , z 2 ) = ( ⃗ x 3 , y 3 , z 3 ) \vec(x1,y1,z1) \times \vec(x2,y2,z2)=\vec(x3,y3,z3) ( x1,y1,z1)×( x2,y2,z2)=( x3,y3,z3)就是以下矩阵的行列式。

红色是原始表格白色是扩展后的结果

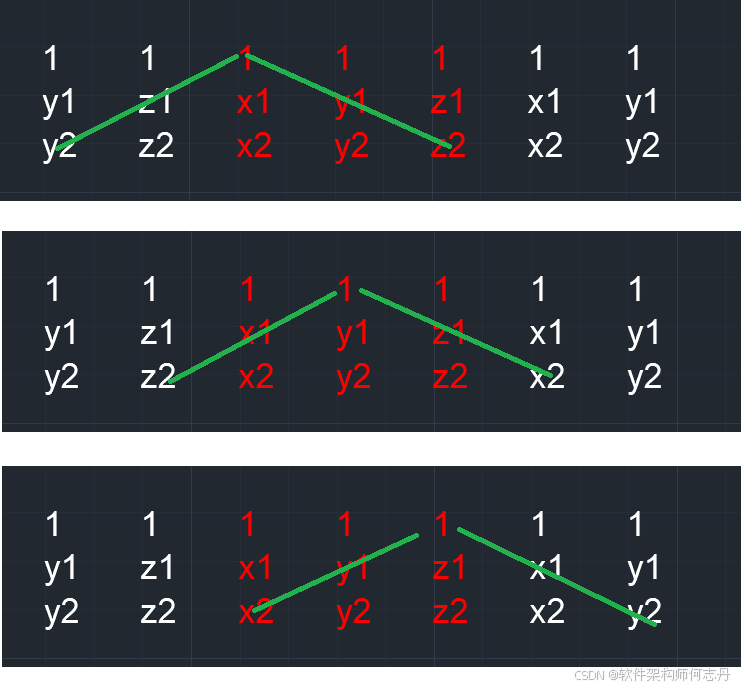
x3 = y1z2-y2z1
y3 = x2z1-x1z2
z3 = x1y2-x2y1
运算的结果是矢量:
方向 :垂直于两个矢量,遵守右手定理。
模长:扫过的有向面积。
二维向量
令 z 1 = z 2 = 0 z_1=z_2=0 z1=z2=0,则x3=0,y3=0,z3不变。
逆时针为真,顺时针为负。
鞋带公式(高斯面积公式)
对于顶点为 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ... , ( x n , y n ) (x_1, y_1), (x_2, y_2), \dots, (x_n, y_n) (x1,y1),(x2,y2),...,(xn,yn) 的简单多边形,其有向面积 A A A 由鞋带公式给出:
A = 1 2 ∣ ∑ i = 1 n x i y i + 1 − x i + 1 y i ∣ A = \frac{1}{2} \left| \sum_{i=1}^{n} x_i y_{i+1} - x_{i+1} y_i \right| A=21∣∑i=1nxiyi+1−xi+1yi∣
如果S > 0,这些端点是逆时针。
如果S< 0,这些端点是顺时针。
∣ S ∣ |S| ∣S∣才是实际面积。
证明比较复杂,就不证明了,弄张图帮助理解。
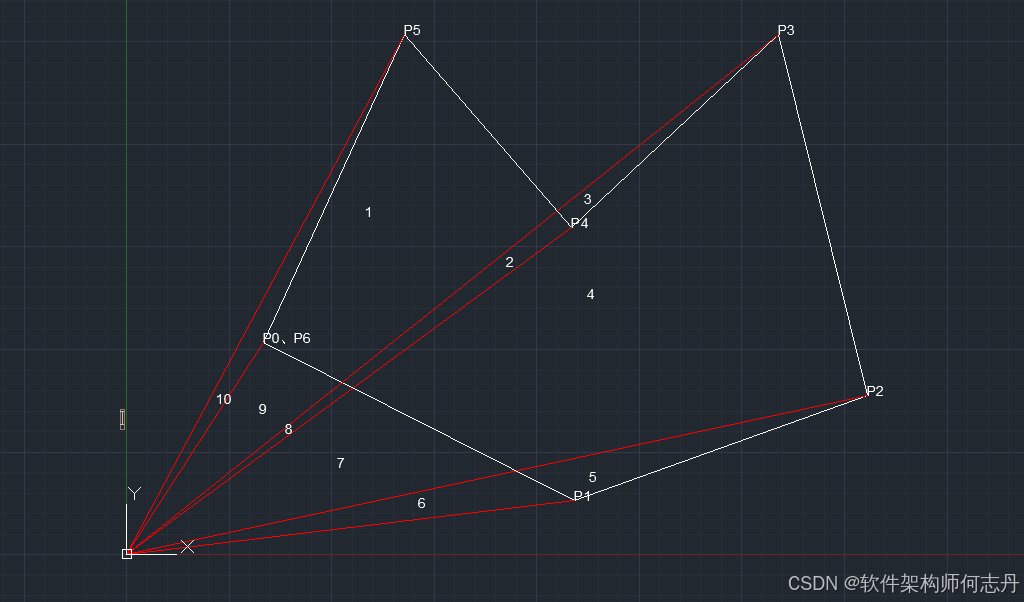
O P 0 ⃗ × O P 1 ⃗ 负 \vec{OP0}\times \vec{OP1} 负 OP0 ×OP1 负包括区域:9,8,7,6。
O P 1 ⃗ × O P 2 ⃗ 正 \vec{OP1}\times \vec{OP2} 正 OP1 ×OP2 正:5,6。
O P 2 ⃗ × O P 3 ⃗ 正 \vec{OP2}\times \vec{OP3} 正 OP2 ×OP3 正:4,7,2,3,8
O P 3 ⃗ × O P 4 ⃗ 负 \vec{OP3}\times \vec{OP4} 负 OP3 ×OP4 负 8,2,3
O P 4 ⃗ × O P 5 ⃗ 正 \vec{OP4}\times \vec{OP5} 正 OP4 ×OP5 正 2,8,1,9,10
O P 5 ⃗ × O P 0 ⃗ 负 \vec{OP5}\times \vec{OP0}负 OP5 ×OP0 负:10
10:+1-1=0
9:-1+1 =0
8:-1+1-1+1=0
7:-1+1=0
6:-1+1=0
5:+1
4:+1
3:+1-1=0
2:+1-1+1=1
1:+1
总结:多边形外部相互抵消,内部正负抵消后余1。
简单多边形P拆分三角形求有向面积
简单多边形P的顶点顺时针分别为ABCDEF ⋯ \cdots ⋯
删除AB、BC,连通AC。余下的简单多边形为Q(如下图的ACDE)。
如果<ABC < 18 0 ∘ 180^\circ 180∘
P的面积=Q的面积+ABC的面积。由于三者的有向面积都为负。
故:P的有向面积=Q的有向面积+ △ A B C \triangle ABC △ABC的有向面积。
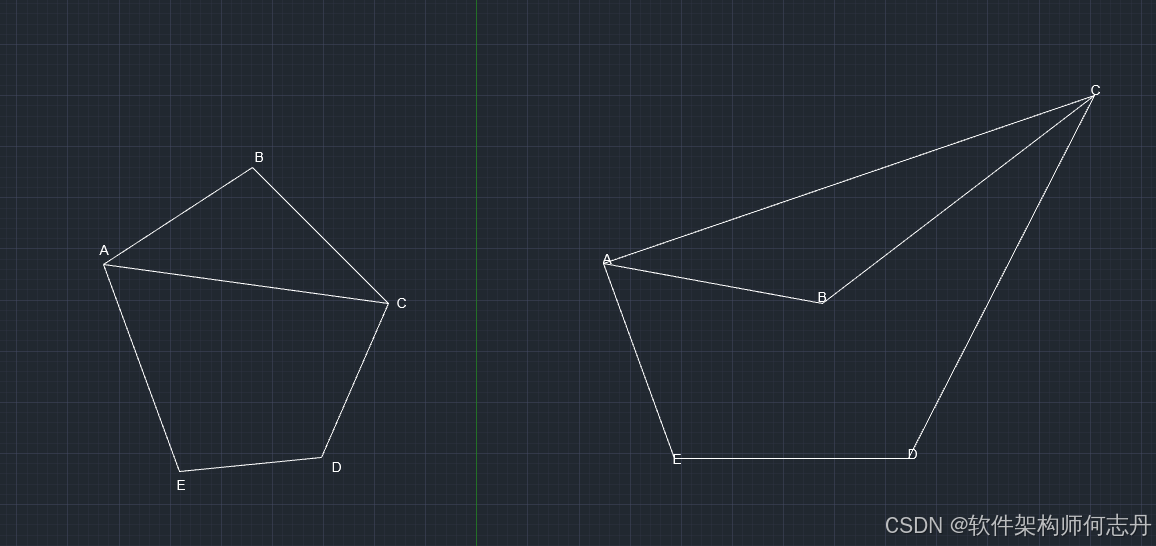
如果 ∠ A B C > 18 0 ∘ \angle ABC>180^\circ ∠ABC>180∘
P的面积+ △ A B C \triangle ABC △ABC面积=Q的面积
由于PQ的面积是负数, △ A B C \triangle ABC △ABC是正。
故:P的有向面积=Q的有向面积+ △ A B C \triangle ABC △ABC的有向面积。
如果 ∠ A B C = = 18 0 ∘ \angle ABC==180^\circ ∠ABC==180∘,ABC的面积为0。
总结 :Q的有向面积=P的有向面积- △ A B C \triangle ABC △ABC的有向面积。
注意:假设求PQ的有向面积,节点顺时针。
二维叉乘的几何证明
正弦定理
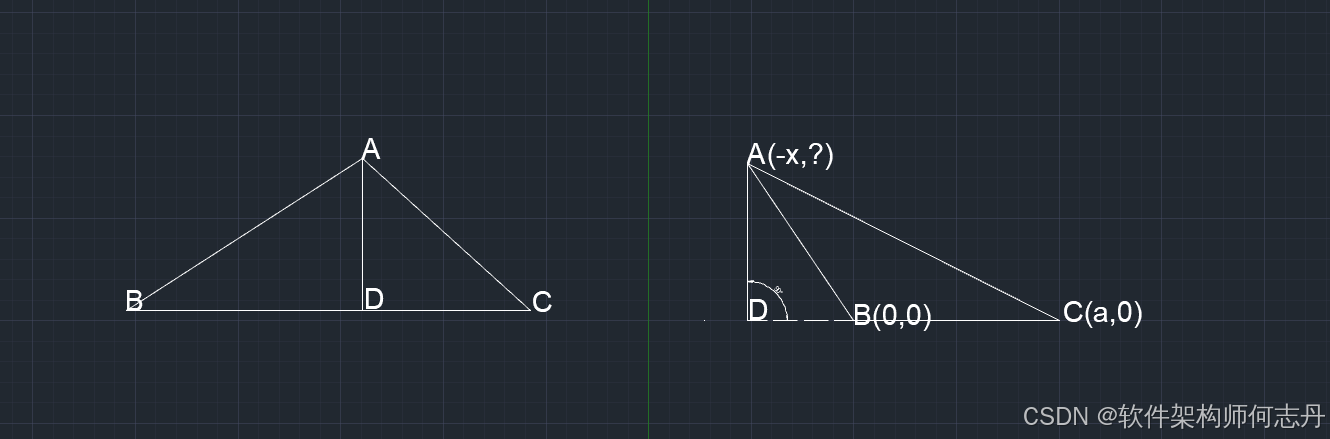
|AD|=c\sinb=b\sinc
同理csina=asinc asinb=bsina
二维叉乘的证明
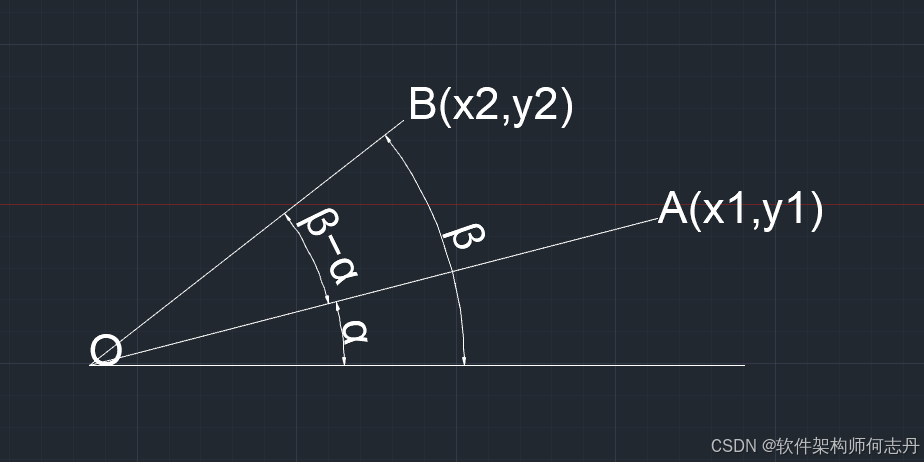
u ⃗ = O ⃗ A , v ⃗ = O ⃗ B \vec u=\vec OA,\vec v=\vec OB u =O A,v =O B
根据正弦公式:
sin α = y 1 ÷ ∣ u ∣ , cos α = x 1 ÷ ∣ u ∣ \sin\alpha=y1\div |u|,\cos \alpha= x1 \div |u| sinα=y1÷∣u∣,cosα=x1÷∣u∣
sin β = y 2 ÷ ∣ v ∣ , cos β = x 2 ÷ ∣ v ∣ \sin\beta=y2\div |v|,\cos \beta= x2 \div |v| sinβ=y2÷∣v∣,cosβ=x2÷∣v∣
∣ u ∣ ∣ v ∣ sin ( β − a l p h a ) = ∣ u ∣ ∣ v ∣ ( sin β cos α − sin α cos β ) 三角函数的和差公式 = ∣ u ∣ ∣ v ∣ ( y 2 x 1 − x 1 y 2 ) ÷ ( ∣ u ∣ ∣ v ∣ ) = x 1 y 2 − x 2 y 1 |u||v|\sin(\beta-alpha)=|u||v|(\sin\beta\cos\alpha-\sin\alpha\cos\beta) 三角函数的和差公式 \\ =|u||v|(y2x1-x1y2)\div (|u||v|)\\ =x1y2-x2y1\\ ∣u∣∣v∣sin(β−alpha)=∣u∣∣v∣(sinβcosα−sinαcosβ)三角函数的和差公式=∣u∣∣v∣(y2x1−x1y2)÷(∣u∣∣v∣)=x1y2−x2y1

扩展阅读
| 我想对大家说的话 |
|---|
| 工作中遇到的问题,可以按类别查阅鄙人的算法文章,请点击《算法与数据汇总》。 |
| 学习算法:按章节学习《喜缺全书算法册》,大量的题目和测试用例,打包下载。重视操作 |
| 有效学习:明确的目标 及时的反馈 拉伸区(难度合适) 专注 |
| 员工说:技术至上,老板不信;投资人的代表说:技术至上,老板会信。 |
| 闻缺陷则喜(喜缺)是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
| 失败+反思=成功 成功+反思=成功 |
视频课程
先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法 用**C++**实现。
