目录
1.各种链表的静态实现
为什么要学会链表的静态实现?
由于静态链表(数组实现)的代码量远少于动态链表(指针+结构体),同时存储密度比较低,所以在算法竞赛中,一般都会使用静态链表
单链表:
cpp
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int e[N], ne[N], p, id, mp[N];//mp数组,下标为元素,值为元素存放位置
void push_front(int x)
{
id++;
e[id] = x;
mp[x] = id;
ne[id] = ne[p];
ne[p] = id;
}
void print()
{
for(int i = ne[p];i;i = ne[i])
{
cout << e[i] << " ";
}
cout << endl << endl;
}
int find(int x)
{
//解法一
//for (int i = ne[p];i;i = ne[i])
//{
// if (e[i] == x)return i;
//}
//return 0;
//解法二
return mp[x];
}
void del(int cur)
{
if (ne[cur])
{
mp[e[ne[cur]]] = 0; //把下一个位置的元素下标值为空
ne[cur] = ne[ne[cur]];
}
}
int main()
{
for (int i = 1;i <= 5;i++)
{
push_front(i);
print();
}
del(4);
print();
cout << find(3) << endl;
return 0;
}代码解释:
两个足够大的数组:
- 一个数组 e 存放数据,充当数据域
- 一个数组 ne 存放下一个元素的下标,充当指针域;每个模拟结点的 ne 数组存放着下一个模拟结点的 下标
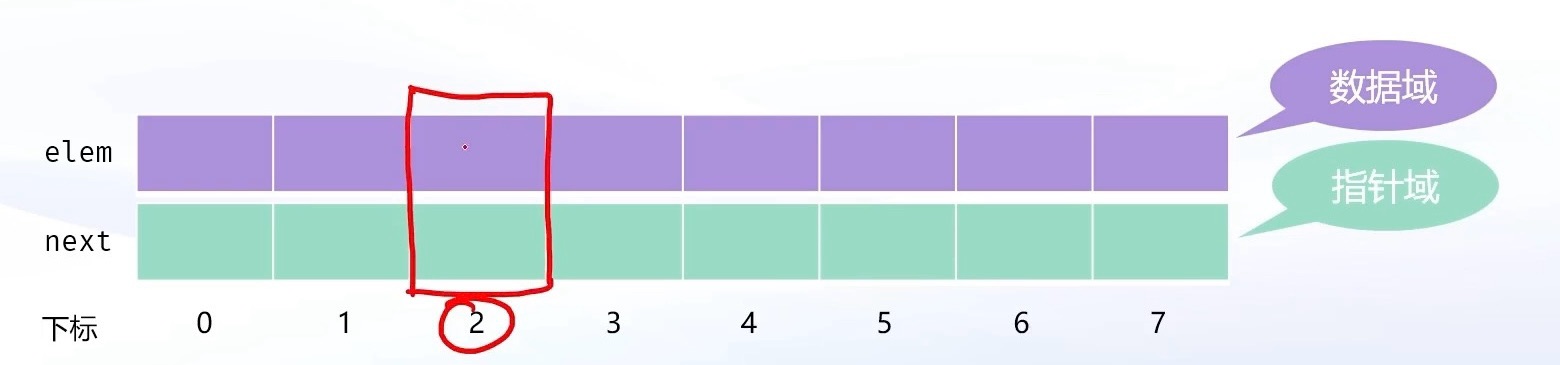
如下图所示,静态链表的一个结点当中有 2 个数组,每个数组下标充当 1 个结点,每个结点会有 e 与 ne 两个数组
两个变量:
- 一个变量 h 标记头结点的下标(可以把下标为 0 的结点视为头结点)
- 一个变量 id 标记新来结点的存储位置(尾节点的后一个结点)
注:用 0 来模拟 NULL,即无效 next
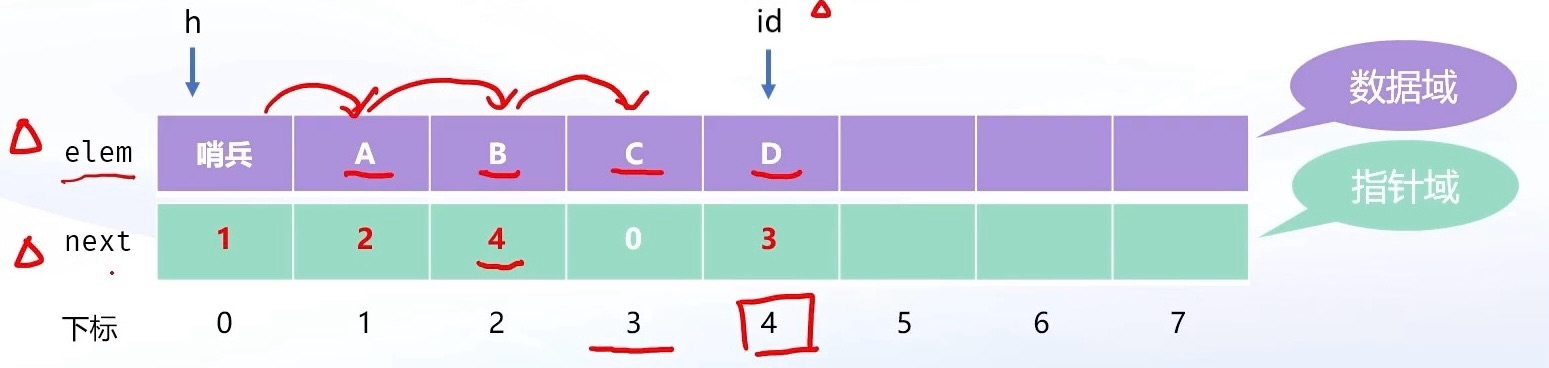
如上图所示,当我们要在 B、C 之间插入 D 时,让 D 的 next 指向 3 下标(C结点),B 的 next 指向 4 下标(D结点)
单链表功能实现注意点:
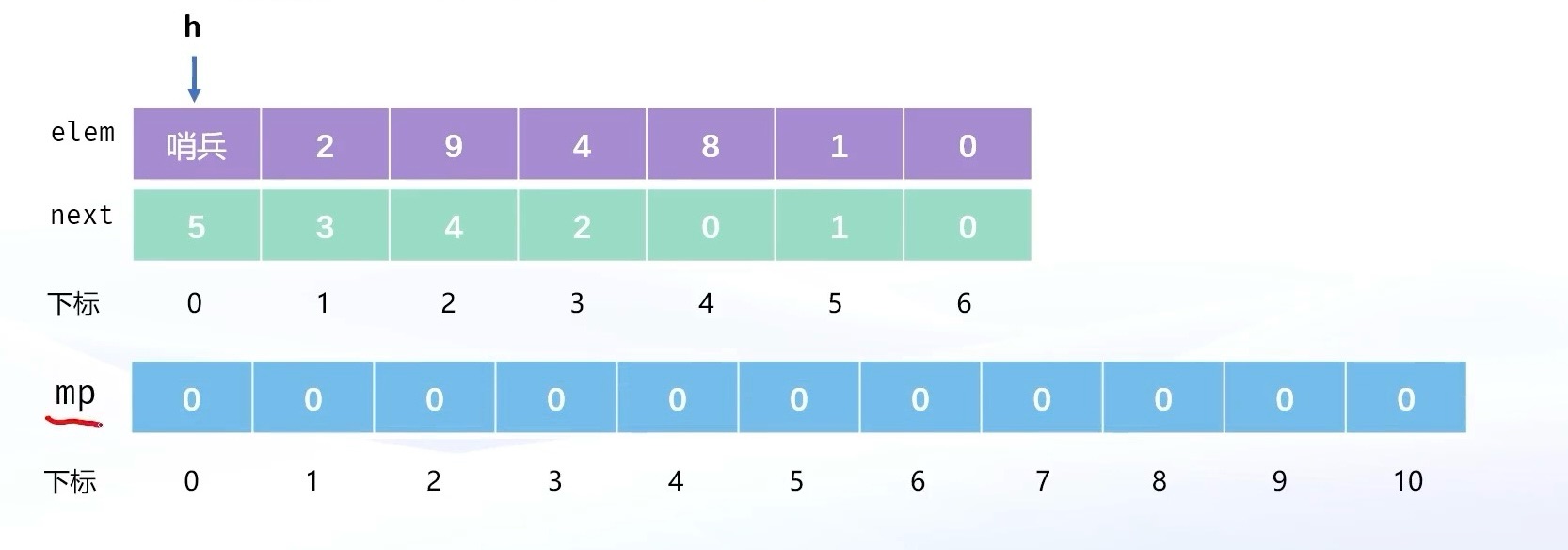
- 按值查找时可以有两个办法,第一种是遍历整个链表,一个一个依次对比;第二种是创建一个 mp 数组,模仿键值对 <元素值,元素所在位置> (如下图所示)
- 在删除时,记得要把 mp 数组当中的元素对应关系变为无效
- 遍历链表打印时,一定要根据 ne 下标来跳着打印,如果只是从头到尾依次输出 e 数组里的值,会把无效值也打印
- 指定位置后插入即把头插中的 h 换为 cur(指定位置)
注:mp数组来优化按值查找时,只能在元素唯一的情况,例如下标4、下标8都存放了元素100,这种时候就不能用mp数组来优化
双链表:
cpp
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int ne[N], e[N], pre[N], p, id, mp[N];
void push_front(int x)
{
id++;
e[id] = x;
mp[x] = id;
ne[id] = ne[p];
pre[id] = p;
pre[ne[p]] = id;
ne[p] = id;
}
void print()
{
for (int i = ne[p];i;i = ne[i])
cout << e[i] << " ";
cout << endl << endl;
}
void insert_back(int x,int cur)//在cur位置后插入结点,结点的值为x
{
id++;
e[id] = x;
mp[x] = id;
ne[id] = ne[cur];
pre[id] = cur;
pre[ne[cur]] = id;
ne[cur] = id;
}
void insert_front(int x, int cur)
{
id++;
e[id] = x;
mp[x] = id;
ne[id] = cur;
pre[id] = pre[cur];
ne[pre[cur]] = id;
pre[cur] = id;
}
int find(int x)
{
return mp[x];
}
void erase(int cur)//删除cur位置元素
{
pre[ne[cur]] = pre[cur];
ne[pre[cur]] = ne[cur];
}
int main()
{
for (int i = 1;i <= 5;i++)
{
push_front(i);
print();
}
insert_front(300, 5);
erase(1);
print();
return 0;
}与单链表相比,双链表多出了pre数组,即每个结点指向前面的指针
也正因为有了指向前面的指针,所以得以删除cur时可以不用去找到其前驱节点,直接删除cur结点本身
循环链表:
因为静态数组实现时,最后一个结点的next指向0,即指向头结点,所以已经满足了循环链表的性质
2.list介绍
cpp
#include<iostream>
#include<list>
using namespace std;
void print(list<int>& l)
{
for(auto x:l) cout<<x<<" ";
cout<<endl;
}
int main()
{
list<int> l;
for(int i=1;i<=5;i++)
{
l.push_back(i);
print(l);
}
for(int i=1;i<=5;i++)
{
l.push_front(i);
print(l);
}
for(int i=1;i<=5;i++)
{
l.pop_back();
print(l);
}
for(int i=1;i<=5;i++)
{
l.pop_front();
print(l);
}
return 0;
}
list 是 c++ stl 库中提供的动态链表模板,主要有以下几个函数功能
- 初始化:list<size> list_name
- push_back:尾插
- pop_back:尾删
- push_front:头插
- pop_front:头删
3.洛谷---排队顺序
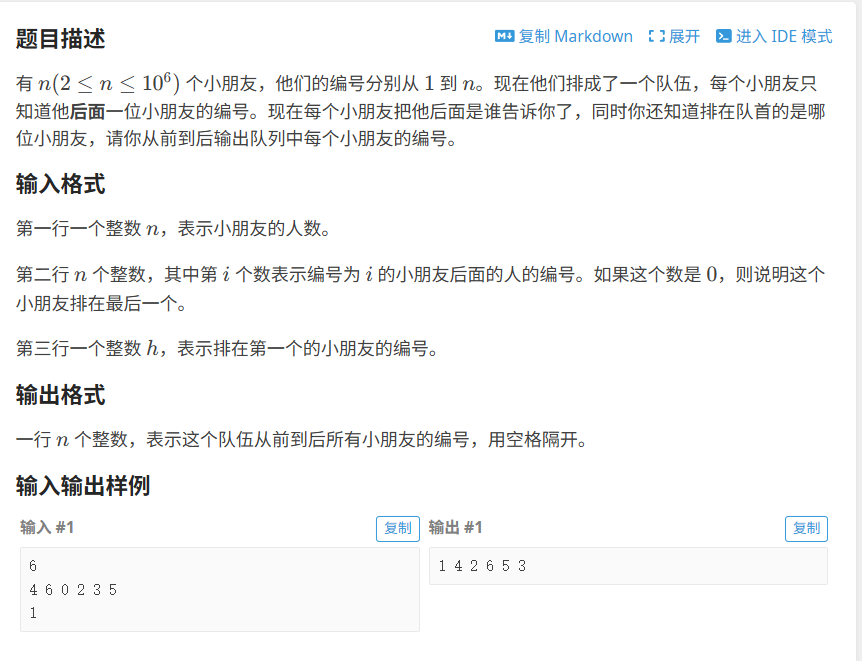
如下图所示,不难发现小朋友编号即为静态数组中的next指针,而下标就可以看成是元素(元素与下标一一对应),1下标对应的next指针为 4,所以是 1 4;4下标对应的next为2,所以是 1 4 2......
拓展到一般情况,第一个小朋友的编号为 h,h 的 next指针为 a[h],最后一个小朋友的next指针 a[h] = 0
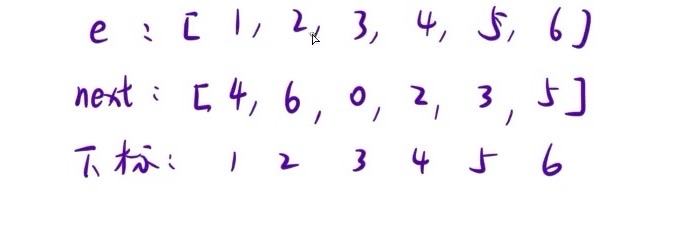
代码:
cpp
#include<iostream>
using namespace std;
int main()
{
int n;cin>>n;
int a[n+1]={0};
for(int i=1;i<=n;i++)cin>>a[i];
int h;cin>>h;
for(int i=h;i;i=a[i]) cout<<i<<" ";//a中存放next指针
return 0;
}4.洛谷---单向链表
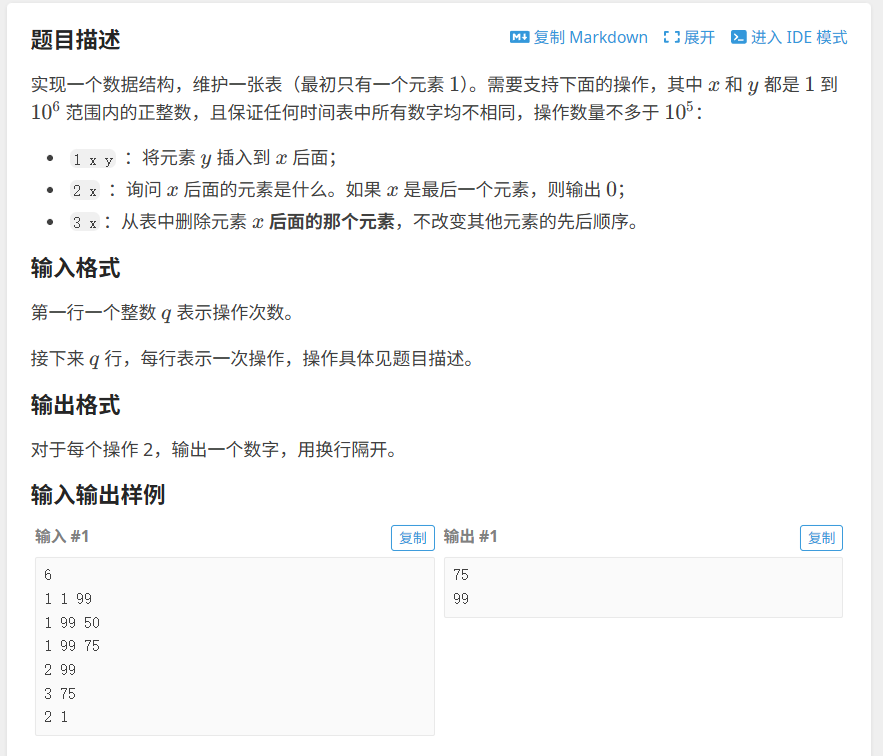
模拟实现一个单链表
操作1为指定位置后插入,操作2为查询指定位置后元素,操作3为删除指定位置后元素
所有数字均不相同,可以使用mp数组优化
代码:
cpp
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int ne[N],e[N],phead,id,mp[N];
int find(int x)
{
return mp[x];
}
void insert_back(int x,int y)//在x元素后插入y元素,先得找到x元素位置
{
int cur = find(x);
id++;
e[id]=y;
mp[y]=id;
ne[id]=ne[cur];
ne[cur]=id;
}
int find_ret(int x)
{
int cur = find(x);
if(ne[cur])
{
return e[ne[cur]];
}
return 0;
}
void erase(int x)
{
int cur = find(x);
if(ne[cur])
{
mp[e[ne[cur]]] = 0;
ne[cur] = ne[ne[cur]];
}
}
int main()
{
int x,y;
int q;cin>>q;
insert_back(phead,1);
while(q--)
{
int in;cin>>in;
if(in == 1)
{
cin>>x>>y;
insert_back(x,y);
}
else if(in == 2)
{
cin>>x;
cout<<find_ret(x)<<endl;
}
else
{
cin>>x;
erase(x);
}
}
return 0;
}5.洛谷---队列安排

现有1个同学进入,然后编号为2~N的同学依次进入,可以指定编号为 i 的同学站在编号为 1~N 中某位同学(先前已经入列)的左边或右边,左边 p = 0,右边 p = 1
然后去掉M个同学,如果指定删除的同学不在队列中,忽略本次操作
通过链表来解决这个问题,指定位置的插入与删除,但考虑到插入可以是结点的左边也可以是其右边(如下图所示),所以需要通过双向链表来解决,即有前驱指针(左插入)与后继指针(右插入)
所以本题就是模拟实现一个双向链表,小朋友编号唯一,所以可以用mp数组优化
代码:
cpp
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int ne[N],e[N],phead,id,mp[N],pre[N];
int find(int x)
{
return mp[x];
}
void insert_back(int x,int y)
{
int cur = find(x);
id++;
e[id]=y;
mp[y]=id;
ne[id]=ne[cur];
pre[id]=cur;
pre[ne[cur]]=id;
ne[cur]=id;
}
void insert_front(int x,int y)
{
int cur = find(x);
id++;
e[id]=y;
mp[y]=id;
ne[id]=cur;
pre[id]=pre[cur];
ne[pre[cur]]=id;
pre[cur]=id;
}
void erase(int x)
{
int cur = find(x);//删除当前元素
if(cur)
{
mp[e[cur]]=0;
ne[pre[cur]]=ne[cur];
pre[ne[cur]]=pre[cur];
}
}
void print()
{
for(int i=ne[phead];i;i=ne[i]) cout<<e[i]<<" ";
}
int main()
{
int n;cin>>n;
n--;
insert_back(phead,1);
int num = 2;
while(n--)
{
int k,p;cin>>k>>p;
if(p)insert_back(k,num);
else insert_front(k,num);
num++;
}
int m;
cin>>m;
while(m--)
{
int del;cin>>del;
erase(del);
}
print();
return 0;
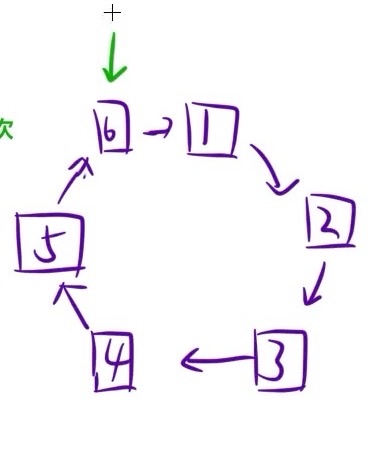
}6.洛谷---约瑟夫问题
实现一个循环链表,即 ptail -> next = phead 的链表(最后一个结点指向头结点)
然后每间隔 m 个结点,删除一个数,同时打印那个被删掉的数
因此本题需要模拟实现一个循环链表
代码:
cpp
#include<iostream>
using namespace std;
const int N = 110;
int ne[N];
int main()
{
int n,m;cin>>n>>m;
for(int i=1;i<n;i++)ne[i]=i+1;
ne[n]=1;
int t=n;
for(int i=1;i<=n;i++)//n次出圈操作
{
for(int j=1;j<m;j++)//让j往后移动m-1位
t = ne[t];
cout<<ne[t]<<" ";//打印当前结点的下一个结点
ne[t] = ne[ne[t]];//删除当前结点的下一个结点
}
return 0;
}代码解释:
- 因为用的是单链表的循环链表,所以删除时需要先找到删除结点的前一个结点,即每次循环到 m-1 然后把 m 删除
- 如果循环链表使用头结点,那么 删除结点 将会很难判断,因为是否会经过 头结点 是不确定的,所以我们选择不使用 头结点
- 如下图所示,初始化时可以指向整个链表的表尾,把 表尾 作为开始就相当于把 表尾 看作了一个有值的 头结点;我们把表尾结点的值搞成1,表头结点的值从2开始
- 因为循环链表的 结点值 是 [1,2,3,......],与下标对应,所以无需要数据域与id来实现静态链表的插入过程了
- 每次 t 往后移动,都是在链表中的结点与结点之间移动,千万不要是遍历数组的方式移动