Hi,大家好,我是半亩花海。在上节说明了迁移学习领域的一些基本知识,那么对迁移学习的问题进行简单的形式化之后,本文主要将介绍迁移学习的总体思路 和常用度量准则****(这里先说明距离和相似度)。核心思路是寻找源领域与目标领域的相似性(不变量)并加以利用。常用的距离度量包括欧氏距离、闵可夫斯基距离和马氏距离;相似度度量则涵盖余弦相似度、互信息、皮尔逊相关系数和Jaccard相关系数。这些度量方法对设计迁移学习算法至关重要,旨在定量评估领域相似性并指导学习过程优化。
目录
[2.1 常见的几种距离](#2.1 常见的几种距离)
[2.2 相似度](#2.2 相似度)
[(4)Jaccard 相关系数](#(4)Jaccard 相关系数)
一、总体思路
形式化之后,我们可以进行迁移学习的研究。迁移学习的总体思路可以概括为:++开发算法来最大限度地利用有标注的领域的知识,来辅助目标领域的知识获取和学习。++
迁移学习的核心是,找到源领域和目标领域之间的相似性 ,并加以合理利用。这种相似性非常普遍。比如,不同人的身体构造是相似的;自行车和摩托车的骑行方式是相似的;国际象棋和中国象棋是相似的;羽毛球和网球的打球方式是相似的。这种相似性也可以理解为不变量。以不变应万变,才能立于不败之地。
举一个杨强教授经常举的例子来说明:我们都知道在中国大陆开车时,驾驶员坐在左边,靠马路右侧行驶。这是基本的规则。然而,如果在英国、香港等地区开车,驾驶员是坐在右边,需要靠马路左侧行驶。那么,如果我们从中国大陆到了香港,应该如何快速地适应他们的开车方式呢?诀窍就是找到这里的不变量:++不论在哪个地区,驾驶员都是紧靠马路中间。++这就是我们这个开车问题中的不变量。
找到相似性 (不变量),是进行迁移学习的核心。
有了这种相似性后,下一步工作就是,++如何度量和利用这种相似性++。度量工作的目标有两点:一是很好地度量两个领域的相似性,不仅定性地告诉我们它们是否相似,更定量地给出相似程度。二是以度量为准则,通过我们所要采用的学习手段,增大两个领域之间的相似性,从而完成迁移学习。
一句话总结: ++相似性是核心,度量准则是重要手段。++
二、度量准则
度量不仅是机器学习和统计学等学科中使用的基础手段,也是迁移学习中的重要工具。 它的核心就是衡量两个数据域的差异。计算两个向量(点、矩阵)的距离和相似度是许多机器学习算法的基础,有时候一个好的距离度量就能决定算法最后的结果好坏。比如 KNN 分类算法就对距离非常敏感。本质上就是找一个变换使得源域和目标域的距离最小(相似度最大)。所以,相似度和距离度量在机器学习中非常重要。
这里给出常用的度量手段,它们都是迁移学习研究中非常常见的度量准则。对这些准则有很好的理解,可以帮助我们设计出更加好用的算法。用一个简单的式子来表示,度量就是描述源域和目标域这两个领域的距离:
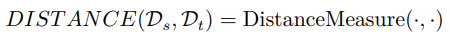
下面我们从距离和相似度度量准则(先说明距离)几个方面进行简要介绍。
2.1 常见的几种距离
(1)欧氏距离
定义在两个向量 (两个点) 上:点 和点
的欧氏距离为:
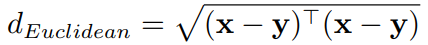
(2)闵可夫斯基距离
Minkowski distance,两个向量(点)的 阶距离:
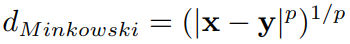
当 时就是曼哈顿距离,当
时就是欧氏距离。
(3)马氏距离
定义在两个向量 (两个点) 上,这两个点在同一个分布里。点 和点
马氏距离为:
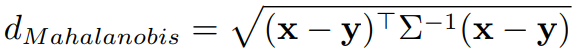
其中, 是这个分布的协方差。
当 时,马氏距离退化为欧氏距离。
2.2 相似度
(1)余弦相似度
衡量两个向量的相关性 (夹角的余弦)。向量 的余弦相似度为:
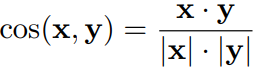
(2)互信息
定义在两个概率分布 上,
。它们的互信息为:
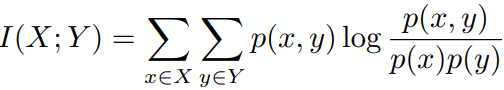
(3)皮尔逊相关系数
衡量两个随机变量的相关性。随机变量 的 Pearson 相关系数为:
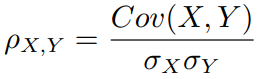
- 理解:协方差矩阵除以标准差之积。
- 范围:
,绝对值越大表示(正/负)相关性越大。
(4)Jaccard 相关系数
对两个集合 ,判断他们的相关性,借用集合的手段:
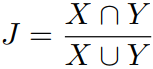
- 理解:两个集合的交集除以并集。
- 扩展:Jaccard 距离
。
三、参考资料
1. 王晋东《迁移学习简明手册》(PDF版) https://www.labxing.com/files/lab_publications/615-1533737180-LiEa0mQe.pdf#page=82&zoom=100,120,392
2. 《迁移学习简明手册》发布啦! https://zhuanlan.zhihu.com/p/35352154