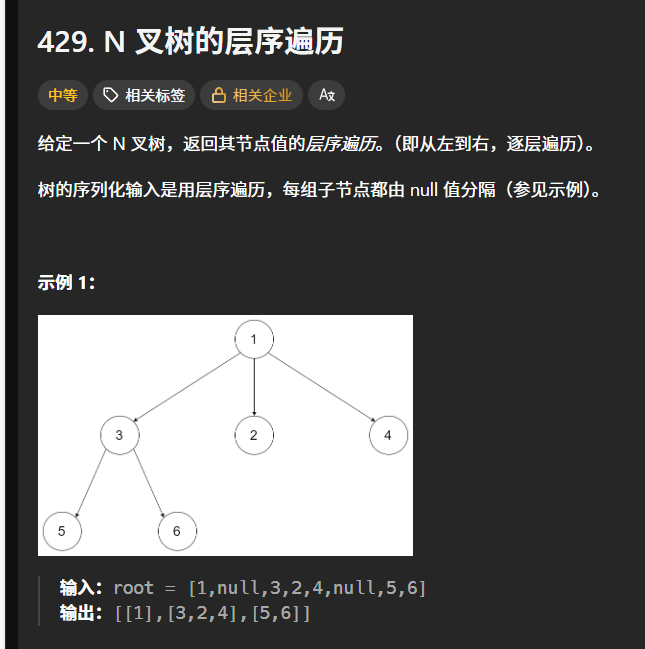
例一
429. N 叉树的层序遍历 - 力扣(LeetCode)先来看这道题:
为什么需要引入队列
因为层序遍历的本质是按 "层" 的顺序处理节点 :先处理第 1 层(根节点),再处理第 2 层(根的所有子节点),接着处理第 3 层(第 2 层每个节点的子节点)......
而队列的特性是 "先进先出",刚好能匹配这种 "按顺序处理、按顺序传递下一层节点" 的逻辑:
- 先把当前层的所有节点依次加入队列;
- 处理当前层时,依次从队列头部取出节点,同时把该节点的所有子节点加入队列尾部;
- 那么当前层的节点全部出队之后,队列里剩下的就是下一层的所有节点。
引入变量来记录当前队列中元素的个数
为什么必须引入这个变量
由于队列本身是 "连续的节点"。
那么我们在处理的过程中很可能出现下面这种情况:
当前层节点还没处理完时,下一层节点已经在往队列里加了。
如果我们不记录 "当前层有多少个节点",那么我们并不知道 "处理到哪个节点时,当前层就结束了"。
反例
以示例一为例,我们假设不记录队列长度,直接循环取队列元素:
初始队列:[1] → 取 1,加子节点 3、2、4 → 队列变成 [3,2,4];
接着取 3,加子节点 5、6 → 队列变成 [2,4,5,6];
再取 2 → 队列变成 [4,5,6]......
那么我们不难发现:当前层(第 2 层)的 3、2、4 还没处理完,下一层(第 3 层)的 5、6 已经入队了。
所以我们根本无法区分 "哪些节点属于第 2 层,哪些属于第 3 层",最终输出的结果会是混乱的 [1,3,2,5,6,4],完全不是层序遍历要求的 "逐层分组"。
这个变量的作用
这个变量的作用是"给当前层画一个'边界"------
它告诉我们:"接下来要处理的count个节点,全是当前层的;处理完这count个,当前层就结束了,那么剩下的队列元素都是下一层的"。
具体流程
- 初始队列:
[1],并记录 count=队列长度=1(这是第 1 层的节点数); - 循环
count次(即处理 1 个节点):- 取
1,并向最终的List<List<Integer>>中加入结果[1]; - 加子节点
3、2、4,队列变成[3,2,4];
- 取
- 循环结束,所以第 1 层处理完成;
- 记录新的count=队列长度=3(这是第 2 层的节点数);
- 循环
count次(处理 3 个节点):- 取
3, 加入结果[3];加子节点5、6→ 队列变成[2,4,5,6]; - 取
2, 加入结果[2];无孩子子节点 → 队列变成[4,5,6]; - 取
4, 加入结果[4];无孩子节点 → 队列变成[5,6];
- 取
- 循环结束 → 第 2 层处理完成(并向最终的List<List<Integer>>中加入结果
[3,2,4]); - 记录新的 count=队列长度=2(这是第 3 层的节点数);
- 循环
count次 ,处理5、6并向最终的List<List<Integer>>中加入结果[5,6];
完整的解题代码
java
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> ret=new ArrayList<>();
if(root==null){
return ret;
}
Queue<Node> q=new LinkedList<>();
q.add(root);
while(!q.isEmpty()){
int count=q.size();
List<Integer> tmp=new ArrayList<>();
for(int i=0;i<count;i++){
Node t=q.poll();
tmp.add(t.val);
for(Node child : t.children){
if(child!=null){
q.add(child);
}
}
}
ret.add(tmp);
}
return ret;
}
}例二
sl103. 二叉树的锯齿形层序遍历 - 力扣(LeetCode)
这道题和上一道题的区别在于:
这题的第偶数层的节点需要逆序存储起来,于是我们可以引入一个flag变量来进行标记当前是偶数层还是奇数层,如果是偶数层,就把该层的结果逆序存储起来。
完整的解题代码
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> ret=new ArrayList<>();
if(root==null){
return ret;
}
int flag=1;
Queue<TreeNode> q=new LinkedList<>();
q.add(root);
while(!q.isEmpty()){
List<Integer> tmp=new ArrayList<>();
int size=q.size();
for(int i=0;i<size;i++){
TreeNode out=q.poll();
tmp.add(out.val);
if(out.left!=null){
q.add(out.left);
}
if(out.right!=null){
q.add(out.right);
}
}
if(flag%2==0){
Collections.reverse(tmp);
}
flag++;
ret.add(tmp);
}
return ret;
}
}例三
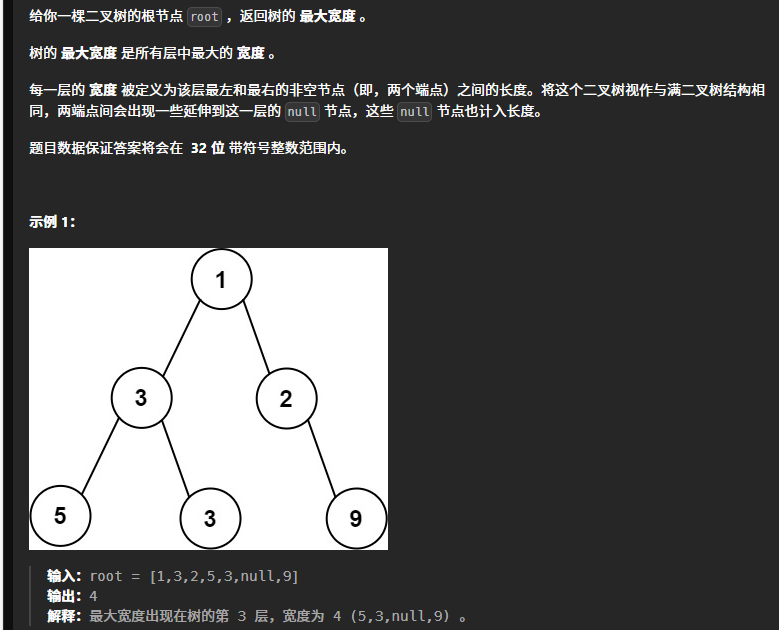
本题要注意的是当一个节点没有左(右)孩子的时候,我们应该要把它给补齐。
我们本题可以借用数组来实现,这个数组中存储的每个元素是一个Pair<TreeNode,Integer>.
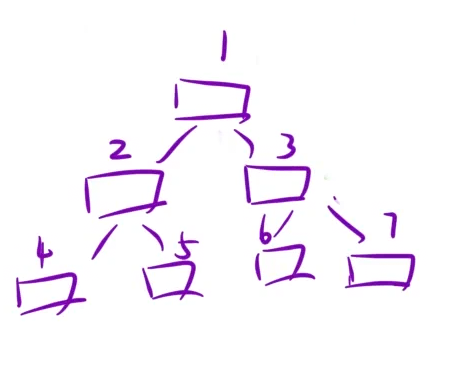
如上图所示,二叉树中的一个节点的编号为x,那么他的左右孩子的编号分别为2x和2x+1.
于是我们就可以借助这个性质,把当前节点以及当前节点的编号都存放在这个Pair中,然后再把这个Pair放到数组当中:
java
List<Pair<TreeNode,Integer>> q=new ArrayList<>();
q.add(new Pair<TreeNode,Integer>(root,1));细节处理
我们借用数组实现队列功能时,为了保持"先进先出"的特性,如果直接在原数组中删除首元素会导致较高时间复杂度。
更高效的做法是:将下一层元素暂存到临时数组中,最后用该临时数组替换原队列q。
易错点
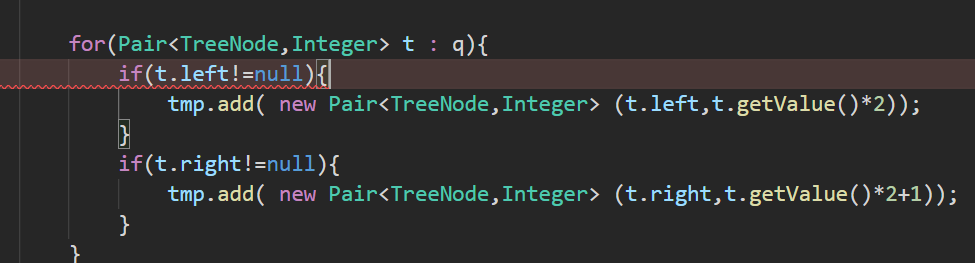
这里我们不应该直接使用t.left,应当像下面这样的方式进行处理:
java
TreeNode node=t.getKey();
int index=t.getValue();
if(node.left!=null){
tmp.add( new Pair<TreeNode,Integer> (node.left,index*2));
}完整的解题代码
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int widthOfBinaryTree(TreeNode root) {
List<Pair<TreeNode,Integer>> q=new ArrayList<>();
q.add(new Pair<TreeNode,Integer>(root,1));
int ret=0;
while(!q.isEmpty()){
//已经进入当前层了,可以把当前层的结果先记录下来
Pair<TreeNode,Integer> first=q.get(0);
Pair<TreeNode,Integer> last=q.get(q.size()-1);
ret=Math.max(ret,last.getValue()-first.getValue()+1);
//接下来让下一层的孩子入队就行,由于本层的节点都在q这个队列里面存储,所以接下来我们只需要遍历这个q队列即可:
List<Pair<TreeNode,Integer>> tmp=new ArrayList<>();
for(Pair<TreeNode,Integer> t : q){
TreeNode node=t.getKey();
int index=t.getValue();
if(node.left!=null){
tmp.add( new Pair<TreeNode,Integer> (node.left,index*2));
}
if(node.right!=null){
tmp.add( new Pair<TreeNode,Integer> (node.right,index*2+1));
}
}
//上面的for循环遍历之后,tmp里面存储的就是下一层的节点元素,那么此时需要把tmp复制给p,来进行下一次的计算宽度的操作。
q=tmp;
}
return ret;
}
}例四
LCR 044. 在每个树行中找最大值 - 力扣(LeetCode)
本题的解法只需在层序遍历的基础之上,引入一个变量来记录当前层的最大值即可。
完整的解题代码
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> largestValues(TreeNode root) {
List<Integer> ret=new ArrayList<>();
if(root==null){
return ret;
}
Queue<TreeNode> q=new LinkedList<>();
q.add(root);
while(!q.isEmpty()){
int result=Integer.MIN_VALUE;
int size=q.size();
for(int i=0;i<size;i++){
TreeNode t=q.poll();
result=Math.max(result,t.val);
if(t.left!=null){
q.add(t.left);
}
if(t.right!=null){
q.add(t.right);
}
}
ret.add(result);
}
return ret;
}
}易错点
记录每层的最大值的result变量应该放在while循环内部,这样才能确保每次进行找最大值之前的result都是最小值。
如果我们把result设置为了全局变量,那么就会跨层复用了上一层的最大值,导致后一层的计算 "起点不对"------ 每一层的最大值应该只基于当前层的节点,而不是基于之前所有层的最大值。
结语
这四道题看似场景各异,但他们的核心思想是高度统一的:
这些算法都基于队列的"先进先出"特性来实现层序遍历:首先利用队列对节点进行分层存储,然后针对每一层节点执行特定业务逻辑(如分组存储、奇偶层逆序、计算节点编号差或求取层内最大值等)。
总结来说,队列是层序遍历的核心基础,而各类业务逻辑只是在这个"逐层处理节点"的通用框架上进行灵活拓展。