从二叉树到衍生结构：5种高频树结构原理+解析

二叉树是数据结构中的核心基础，其衍生出的多种特殊结构（红黑树、Trie树、二叉堆、线段树、霍夫曼树），在工程开发和算法刷题中高频出现。它们各自继承了二叉树的「分治」思想，又针对特定场景做了优化，完美解决了普通二叉树效率瓶颈、功能单一等问题。

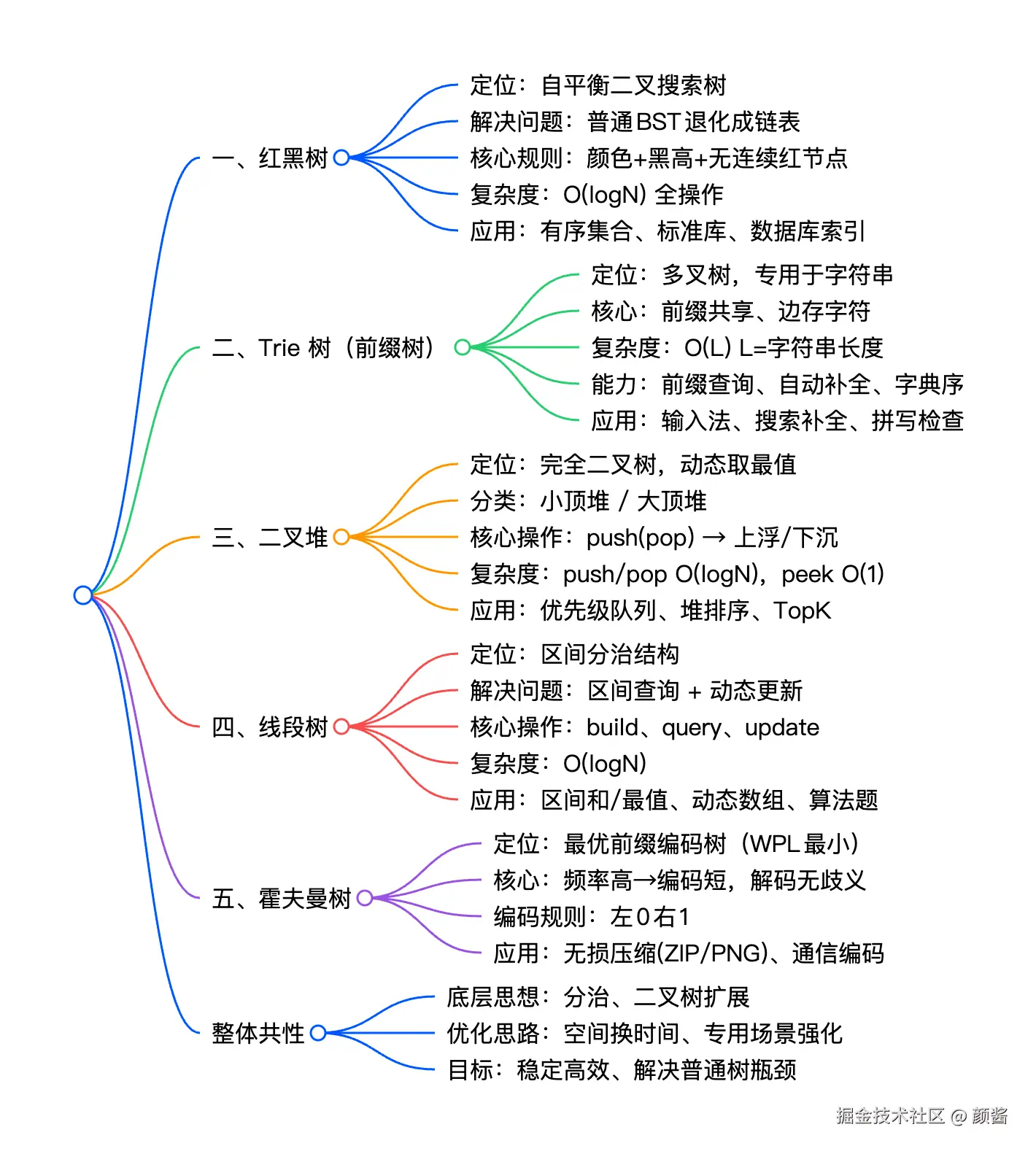
本文将逐一拆解这5种衍生树结构，结合核心原理和代码实现，帮你理清它们的应用场景和底层关联，新手也能快速入门，夯实数据结构基础。

一、红黑树：自平衡的二叉搜索树（完美平衡的实现）

1.1 核心定位

红黑树是一种自平衡的二叉搜索树，核心解决「普通二叉搜索树退化成链表」的痛点------普通二叉搜索树在极端插入顺序下（如从小到大插入），会退化为链表，导致增删查改时间复杂度从O(logN)退化到O(N)；而红黑树通过自身的平衡规则，确保任何时候树高都维持在O(logN)（即「完美平衡」，非绝对平衡，而是树高可控），从而保证所有操作的时间复杂度稳定在O(logN)。

1.2 平衡的核心逻辑

红黑树的平衡不是通过频繁调整节点位置实现的，而是通过「颜色标记」+「旋转操作」（左旋、右旋），维护5条核心规则（确保树高可控）：

每个节点要么是红色，要么是黑色；
根节点必须是黑色；
所有叶子节点（NIL节点，空节点）都是黑色；
如果一个节点是红色，它的两个子节点必须是黑色（避免连续红节点）；
从任意节点到其所有叶子节点的路径，包含的黑色节点数量相同（黑高一致）。

插入/删除节点时，若破坏上述规则，会通过「变色」或「旋转」快速修复（比如红节点冲突时，先尝试变色，变色无效则执行旋转）。无需深究复杂的旋转细节，核心记住：红黑树的「完美平衡」是「树高可控的平衡」，代价是代码实现复杂，但工程中（如Java的TreeMap、HashMap的红黑树部分）已封装好，无需手动实现，这也是其能广泛应用于有序数据维护场景的关键，下文将具体介绍其典型应用。

1.3 应用场景

需要「动态维护有序数据」且「高频增删查改」的场景：

编程语言的标准库（Java TreeMap/TreeSet、C++ map/set）；
Linux内核的进程调度、内存管理；
数据库的索引结构（部分数据库用红黑树优化索引查询）。

二、Trie树（字典树/前缀树）：字符串处理的利器

2.1 核心定位

Trie树（读音/triː/，源自retrieval）是二叉树延伸出的多叉树结构，专门针对字符串优化设计。与哈希表、红黑树不同，Trie树的核心优势是「高效处理字符串前缀相关操作」，同时能节省公共前缀的内存空间。

2.2 核心原理

Trie树的结构可以用一句话总结：每条边代表一个字符，从根到某节点的路径对应一个字符串，节点标记该字符串是否为完整单词。

核心细节：Trie树的结构设计始终围绕"字符串高效处理"和"内存节省"两大核心，其关键细节可拆解为3点：

节点本身不存储字符，字符由「父节点到子节点的边」决定；
节点包含两个关键属性：val（存储字符串对应的值，可选）、children（存储子节点，通常用数组或哈希表实现，如ASCII字符用大小为256的数组，a-z用大小为26的数组）；
公共前缀只存储一次，比如存储"apple"、"app"、"appl"，只需存储"a-p-p-l-e"一条路径，无需重复存储"app"前缀，这也是其节省内存的核心原因，结合下文的代码实现，可更清晰理解这一特性。

2.3 核心优势与应用场景

相比哈希表、红黑树，Trie树的独特优势是「前缀操作高效」，具体如下：

节省存储空间：公共前缀仅存储一次，适合大量重复前缀的字符串（如证件号、单词词典）；
前缀操作高效：最短前缀匹配、最长前缀匹配、前缀查重等操作，时间复杂度均为O(L)（L为前缀长度）；
支持通配符匹配（如"t.a."匹配"that"、"team"），适合搜索引擎关键词匹配；
支持字典序遍历，与红黑树持平，但优于哈希表。

基于以上优势，Trie树的典型应用场景十分广泛，主要集中在字符串相关处理领域：

自动补全（输入法、搜索引擎）；
拼写检查、前缀查重（如用户名前缀校验）；
字典序排序、词频统计；
通配符匹配（简单的关键词搜索）。

2.4 核心代码实现（简化版TrieMap）

javascript 复制代码

// Trie树节点
var TrieNode = function() {
    this.val = null; // 存储键对应的值
    this.children = new Array(256); // 适配所有ASCII字符
};

// TrieMap核心实现（简化版）
var TrieMap = class {
    constructor() {
        this.root = new TrieNode(); // 根节点（空字符）
        this.count = 0; // 键值对数量
    }

    // 插入键值对
    put(key, val) {
        let node = this.root;
        for (let c of key) {
            const idx = c.charCodeAt(0); // 字符转ASCII索引
            if (!node.children[idx]) {
                node.children[idx] = new TrieNode();
            }
            node = node.children[idx];
        }
        node.val = val;
        this.count++;
    }

    // 查询键对应的值
    get(key) {
        let node = this.root;
        for (let c of key) {
            const idx = c.charCodeAt(0);
            if (!node.children[idx]) return null;
            node = node.children[idx];
        }
        return node.val;
    }

    // 判断是否存在前缀为prefix的键
    hasKeyWithPrefix(prefix) {
        let node = this.root;
        for (let c of prefix) {
            const idx = c.charCodeAt(0);
            if (!node.children[idx]) return false;
            node = node.children[idx];
        }
        return true;
    }

    // 获取键值对数量
    size() {
        return this.count;
    }
}

// 测试
const trie = new TrieMap();
trie.put("apple", 1);
trie.put("app", 2);
console.log(trie.get("apple")); // 1
console.log(trie.hasKeyWithPrefix("app")); // true

三、二叉堆：动态排序的核心（优先级队列底层）

3.1 核心定位

二叉堆是一种特殊的完全二叉树，核心功能是「动态排序」------可不断插入、删除元素，且结构会自动调整，确保始终能快速获取最值（最大值/最小值）。它的核心操作只有两个：swim（上浮）和sink（下沉），正是这两个操作维护了堆的核心性质。

二叉堆的两大核心应用：优先级队列（底层实现）、堆排序算法。

3.2 核心原理

二叉堆分为两种，核心性质围绕「父子节点大小关系」：

小顶堆：任意节点的值 ≤ 其左右子节点的值，根节点是最小值；
大顶堆：任意节点的值 ≥ 其左右子节点的值，根节点是最大值。

关键特性：二叉堆是完全二叉树，因此可以用「数组」原地模拟（无需创建TreeNode），通过索引计算父子节点位置，效率更高：

父节点索引：Math.floor((nodeIndex - 1) / 2)；
左子节点索引：nodeIndex * 2 + 1；
右子节点索引：nodeIndex * 2 + 2。

核心操作解析（小顶堆为例）：

push（插入元素）：新元素追加到数组末尾（完全二叉树最右侧），执行swim（上浮）------与父节点比较，若更小则交换，直到满足小顶堆性质或到达根节点；
pop（删除堆顶）：用数组末尾元素覆盖堆顶，执行sink（下沉）------与左右子节点中的最小值比较，若更大则交换，直到满足小顶堆性质或到达叶子节点；
peek（查看堆顶）：直接返回数组[0]（根节点），时间复杂度O(1)。这三大操作共同支撑起二叉堆动态排序、快速取最值的核心功能，下文的代码实现也将围绕这三个操作展开，直观呈现其工作逻辑。

3.3 核心代码实现（小顶堆+优先级队列）

javascript 复制代码

class SimpleMinPQ {
  constructor(capacity) {
    this.capacity = capacity; // 堆最大容量
    this.heap = []; // 数组模拟堆
    this._size = 0; // 实际元素数
  }

  // 获取堆大小
  size() {
    return this._size;
  }

  // 查看堆顶（最小值）
  peek() {
    if (this._size === 0) return null;
    return this.heap[0];
  }

  // 插入元素
  push(val) {
    if (this._size === this.capacity) {
      throw Error('heap is full');
    }
    this.heap[this._size] = val; // 追加到末尾
    this.swim(this._size); // 上浮调整
    this._size++;
  }

  // 删除并返回堆顶
  pop() {
    if (this._size === 0) throw Error('heap is empty');
    const minValue = this.heap[0]; // 保存堆顶值
    this.heap[0] = this.heap[this._size - 1]; // 堆尾覆盖堆顶
    this.sink(0); // 下沉调整
    this._size--;
    return minValue;
  }

  // 上浮：新元素向上调整
  swim(nodeIndex) {
    while (nodeIndex !== 0 && this.heap[nodeIndex] < this.heap[this.parentIndex(nodeIndex)]) {
      this.swap(nodeIndex, this.parentIndex(nodeIndex));
      nodeIndex = this.parentIndex(nodeIndex);
    }
  }

  // 下沉：堆顶元素向下调整
  sink(nodeIndex) {
    while (this.leftChildIndex(nodeIndex) < this._size) {
      let minChildIndex = this.leftChildIndex(nodeIndex);
      const rightChildIndex = this.rightChildIndex(nodeIndex);
      // 找到左右子节点中的最小值
      if (rightChildIndex < this._size && this.heap[rightChildIndex] < this.heap[minChildIndex]) {
        minChildIndex = rightChildIndex;
      }
      // 满足堆性质，停止下沉
      if (this.heap[nodeIndex] <= this.heap[minChildIndex]) break;
      this.swap(nodeIndex, minChildIndex);
      nodeIndex = minChildIndex;
    }
  }

  // 交换两个节点
  swap(index1, index2) {
    [this.heap[index1], this.heap[index2]] = [this.heap[index2], this.heap[index1]];
  }

  // 父节点索引
  parentIndex(nodeIndex) {
    return Math.floor((nodeIndex - 1) / 2);
  }

  // 左子节点索引
  leftChildIndex(nodeIndex) {
    return nodeIndex * 2 + 1;
  }

  // 右子节点索引
  rightChildIndex(nodeIndex) {
    return nodeIndex * 2 + 2;
  }
}

// 测试
const pq = new SimpleMinPQ(6);
pq.push(1);
pq.push(5);
pq.push(7);
pq.push(8);
pq.push(3);
pq.push(2);
console.log(pq.peek()); // 1
console.log(pq.pop()); // 1（删除堆顶）
console.log(pq.size()); // 5

3.4 应用场景

结合二叉堆动态排序、快速取最值的核心特性，其应用场景主要集中在需要动态维护有序数据、快速获取最值的场景：

优先级队列（任务调度、TopK问题、中位数问题）；
堆排序（时间复杂度O(NlogN)，原地排序）；
动态获取最值（如实时数据的最大值/最小值监控）。

四、线段树：区间查询与更新的神器

4.1 核心定位

线段树是二叉树衍生的一种特殊结构，核心解决「数组区间查询+动态更新」的问题。普通前缀和、后缀和虽能快速查询区间和，但更新元素时效率极低（O(N)）；而线段树能将「区间查询」和「单点/区间更新」的时间复杂度均稳定在O(logN)，是处理区间问题的最优结构之一。

4.2 核心原理

线段树的核心思想是「分治+预处理」：将原数组的区间不断拆分，每个节点对应一个区间，存储该区间的「聚合值」（和、最值、积等），查询/更新时只需操作相关区间，无需遍历整个数组。

核心操作解析：

构建（build）：递归拆分区间，非叶子节点的聚合值 = 左子节点聚合值 + 右子节点聚合值（求和场景），叶子节点对应原数组元素；
区间查询（query）：递归判断当前节点区间与目标区间的关系，分为「完全不重叠（返回中性值，如求和返回0）」「完全重叠（返回当前节点值）」「部分重叠（分治查询左右子树，合并结果）」；
单点更新（update）：找到目标叶子节点，更新其值，再向上回溯，更新所有父节点的聚合值（确保区间值正确）。这三个操作相辅相成，实现了线段树高效处理区间问题的核心能力，下文将通过代码实现，具体展示其操作逻辑。

4.3 核心代码实现（求和场景）

javascript 复制代码

class SegmentTree {
  constructor(nums) {
    this.n = nums.length;
    this.tree = new Array(4 * this.n); // 线段树数组，开4*n足够
    this.build(0, 0, this.n - 1, nums); // 构建线段树
  }

  // 构建线段树（node：当前节点索引，l/r：当前节点覆盖区间）
  build(node, l, r, nums) {
    if (l === r) {
      this.tree[node] = nums[l]; // 叶子节点，存储原数组值
      return;
    }
    const mid = Math.floor((l + r) / 2);
    const leftChild = 2 * node + 1;
    const rightChild = 2 * node + 2;
    this.build(leftChild, l, mid, nums); // 递归构建左子树
    this.build(rightChild, mid + 1, r, nums); // 递归构建右子树
    this.tree[node] = this.tree[leftChild] + this.tree[rightChild]; // 合并左右子树值
  }

  // 单点更新（idx：原数组索引，val：新值）
  update(idx, val) {
    this._update(0, 0, this.n - 1, idx, val);
  }

  _update(node, l, r, idx, val) {
    if (l === r) {
      this.tree[node] = val; // 更新叶子节点
      return;
    }
    const mid = Math.floor((l + r) / 2);
    const leftChild = 2 * node + 1;
    const rightChild = 2 * node + 2;
    if (idx <= mid) {
      this._update(leftChild, l, mid, idx, val);
    } else {
      this._update(rightChild, mid + 1, r, idx, val);
    }
    this.tree[node] = this.tree[leftChild] + this.tree[rightChild]; // 回溯更新父节点
  }

  // 区间查询（ql/qr：查询区间）
  query(ql, qr) {
    return this._query(0, 0, this.n - 1, ql, qr);
  }

  _query(node, l, r, ql, qr) {
    if (r < ql || l > qr) return 0; // 完全不重叠，返回0
    if (ql <= l && r <= qr) return this.tree[node]; // 完全重叠，返回当前节点值
    const mid = Math.floor((l + r) / 2);
    const leftChild = 2 * node + 1;
    const rightChild = 2 * node + 2;
    const leftSum = this._query(leftChild, l, mid, ql, qr);
    const rightSum = this._query(rightChild, mid + 1, r, ql, qr);
    return leftSum + rightSum; // 部分重叠，合并结果
  }
}

// 测试
const nums = [1, 3, 5, 7, 9, 11];
const st = new SegmentTree(nums);
console.log(st.query(1, 4)); // 3+5+7+9=24
st.update(2, 6); // 索引2的值从5改为6
console.log(st.query(1, 4)); // 3+6+7+9=25

4.4 应用场景

线段树的核心优势是高效处理区间查询与更新，因此其应用场景主要集中在需要频繁操作区间数据的场景：

区间和、区间最值、区间积的高频查询与更新；
动态数组的区间操作（如股票区间最大涨幅、区间元素修改）；
算法刷题中的区间问题（如力扣307. 区域和检索 - 数组可修改）。

五、霍夫曼树：最优前缀编码（数据压缩核心）

5.1 核心定位

霍夫曼树（最优前缀编码树）是二叉树的经典应用，核心用于「无损数据压缩」。它通过统计字符出现频率，构建一棵「带权路径长度（WPL）最小」的二叉树，基于该树生成的霍夫曼编码，能在保证解码唯一性的前提下，实现最高的压缩率。

5.2 核心原理

先明确两个基础概念：

无损压缩：压缩后的数据可完全还原，无信息丢失（如ZIP压缩）；
变长编码：不同字符的编码长度不同，频率高的字符编码更短（对比ASCII定长编码，节省空间）。

霍夫曼树的核心逻辑是：频率高的字符，放在离根节点更近的位置（编码更短）；频率低的字符，放在离根节点更远的位置（编码更长），以此确保整个树的WPL（所有叶子节点「频率×路径长度」之和）最小，即压缩率最高。

编码规则：左子树为0，右子树为1，根到叶子节点的路径即为字符编码。以字符频率（a:10、b:8、c:9、d:2、e:5）为例，具体编码与WPL计算如下：

a: 0（路径长度1，10×1=10）；
b: 10（路径长度2，8×2=16）；
c: 110（路径长度3，9×3=27）；
d: 1110（路径长度4，2×4=8）；
e: 1111（路径长度4，5×4=20）；
WPL=10+16+27+8+20=81（最小带权路径长度）。

解码唯一性：任意字符的编码，都不是另一个字符编码的前缀（如a的编码0，不会是b的编码10的前缀），确保解码时无歧义，这也是霍夫曼编码能实现无损压缩的关键前提，也奠定了其在数据压缩领域的应用基础。

5.3 应用场景

无损数据压缩（ZIP、PNG图片压缩的核心算法之一）；
文本编码、通信传输（节省带宽，提高传输效率）；
频率相关的最优编码场景（如日志压缩、数据存储优化）。

六、总结：5种树结构的核心对比与关联

这5种树结构均衍生自二叉树，继承了「分治」的核心思想，但针对不同场景做了针对性优化，核心对比如下，可快速理清每种结构的核心差异与适用场景：

数据结构	核心特性	时间复杂度（增删查改/核心操作）	核心应用
红黑树	自平衡二叉搜索树，树高O(logN)	O(logN)（所有操作）	有序数据维护、标准库实现
Trie树	多叉树，优化字符串前缀操作	O(L)（L为字符串长度）	自动补全、前缀查重、字符串编码
二叉堆	完全二叉树，动态排序，快速取最值	O(logN)（push/pop）、O(1)（peek）	优先级队列、堆排序
线段树	区间分治，优化区间查询/更新	O(logN)（查询/更新）	区间操作、动态数组优化
霍夫曼树	最优前缀编码树，WPL最小	O(NlogN)（构建）	无损数据压缩、通信编码
核心关联：所有结构都围绕「二叉树的分治思想」展开，通过「空间换时间」的思路优化效率------红黑树用颜色标记换平衡，Trie树用多叉结构换字符串操作效率，线段树用区间预处理换区间操作效率，霍夫曼树用频率排序换压缩率。它们虽应用场景不同，但底层逻辑均源于二叉树，掌握这种分治思维，能更轻松理解各类衍生数据结构的设计思路，也能更精准地选择合适的结构解决实际问题。

对于新手而言，无需急于掌握所有结构的代码实现，重点理解每种结构的「应用场景」和「核心原理」，刷题或开发时，能根据需求快速选择合适的数据结构，就是最大的收获。后续可针对具体结构（如红黑树、霍夫曼树）深入研究代码实现，夯实细节。