C#验证拉马努金圆周率公式

拉马努金圆周率

1914年，印度天才数学家斯里尼瓦瑟·拉马努金在他的论文里发表了一系列共14条圆周率的计算公式。

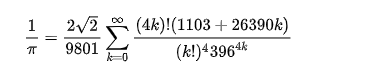
这个公式每计算一项可以得到8位的十进制精度。

Ramanujan圆周率

当K=0时 π=9801/(1103*sqrt(8))

新建控制台应用程序RamanujanPi

示例程序：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
/*
 * 拉马努金圆周率公式 Ramanujan Pi
 * ​
1914年，印度天才数学家【斯里尼瓦瑟·拉马努金】在他的论文里发表了一系列共14条圆周率的计算公式。
这个公式每计算一项可以得到8位的十进制精度。​
因double类型小数点后最多14位精度，实际计算出来有一定误差
*/

namespace RamanujanPi
{
    class Program
    {
        static void Main(string[] args)
        {
            for (int k = 0; k < 8; k++)
            {
                CalculatePi(k);
            }
            Console.ReadLine();
        }

        /// <summary>
        /// 计算圆周率
        /// </summary>
        /// <param name="k"></param>
        /// <returns></returns>
        static void CalculatePi(int k) 
        {
            double addition = CalculateOneItem(0);
            for (int i = 1; i <= k; i++)
            {
                addition += CalculateOneItem(k);
            }
            //计算出反比例1/π
            double inverseProportion = Math.Sqrt(8) / 9801 * addition;
            double pi = 1 / inverseProportion;
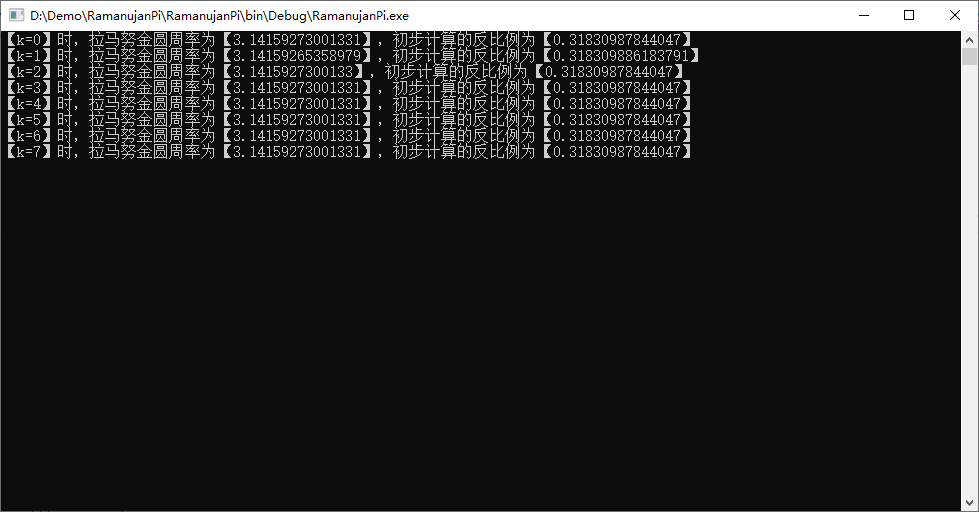
            Console.WriteLine($"【k={k}】时，拉马努金圆周率为【{pi}】，初步计算的反比例为【{inverseProportion}】");
        }

        /// <summary>
        /// 计算拉马努金圆周率的某一个项
        /// </summary>
        /// <param name="k"></param>
        /// <returns></returns>
        static double CalculateOneItem(int k) 
        {
            if (k < 0) 
            {
                throw new ArgumentException("参数k必须为自然数，【0,1,2,3,...】");
            }
            if (k == 0) 
            {
                return 1103;
            }
            return Factorial(4 * k) * (1103 + 26390 * k) / (Math.Pow(Factorial(k), 4) * Math.Pow(396, 4 * k));
        }

        /// <summary>
        /// 阶乘：数学术语。 一个正整数的阶乘（factorial）是所有小于及等于该数的正整数的积，并且0的阶乘为1。自然数n的阶乘写作n!
        /// </summary>
        /// <param name="k">正整数</param>
        /// <returns></returns>
        static long Factorial(int k) 
        {
            if (k <= 0) 
            {
                return 1;
            }
            long factorial = 1;
            for (int i = 1; i <= k; i++)
            {
                factorial = factorial * i;
            }
            return factorial;
        }
    }
}

运行如图：